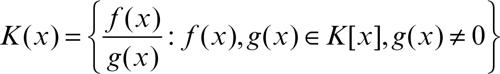quozienti, campo dei

quozienti, campo dei

quozienti, campo dei o campo delle frazioni, in algebra, relativamente a un dominio d’integrità D è il minimo campo che lo contiene. Solitamente esso è indicato con il simbolo Q(D). Essere un dominio d’integrità è condizione necessaria e sufficiente per un anello affinché esso possa essere immerso in un campo (→ immersione). È dunque possibile pensare a un dominio d’integrità come a un “campo incompleto”, nel senso che esso non possiede abbastanza elementi per essere un campo. Esiste un modo canonico di costruire il campo dei quozienti di un dato dominio D: euristicamente, bisogna aggiungere gli elementi mancanti, cioè tutti gli inversi moltiplicativi degli elementi non nulli non invertibili in D. In aggiunta, volendo conservare la chiusura rispetto alle operazioni di addizione e moltiplicazione, sarà necessario aggiungere tutti i rapporti (o frazioni) di elementi di D.

Se D₀ = D − {0}, formalmente si definisce il campo dei quozienti del dominio D come l’insieme quoziente Q(D) = (D × D₀)/∼, dove ∼ è la relazione di equivalenza definita sul prodotto cartesiano D × D₀ come segue:

Usando la notazione frazionaria, la classe di un elemento (a, b) in D × D₀ è solitamente indicata mediante la frazione a /b. Su Q(D) si definisce dunque una struttura di campo fornendolo delle due operazioni di addizione + e di moltiplicazione ⋅ definite come segue, dove a, b, c e d sono generici elementi di D, con b e d non nulli:

Tali operazioni posseggono come elementi neutri rispettivamente le classi 0 = 0/1 e 1 = 1/1. Il dominio D risulta naturalmente immerso come sottoanello di Q(D), mediante l’omomorfismo naturale i: D → Q(D) definito da i(a) = a /1. In questo senso, ogni elemento non nullo a di D risulta invertibile in Q(D), con inverso 1/a. Il procedimento mediante cui si costruisce il campo dei quozienti di un dominio d’integrità D ricalca da vicino la costruzione formale dell’insieme dei numeri razionali Q a partire dall’insieme dei numeri interi Z; in effetti Q coincide con il campo dei quozienti di Z. Un secondo importante esempio è il campo dei quozienti dell’anello dei polinomi K[x] a coefficienti in un campo K: esso è detto il campo delle funzioni razionali a coefficienti in K ed è indicato con il simbolo K(x). Il suo generico elemento sarà un rapporto di due polinomi a coefficienti in K, di cui il secondo non identicamente nullo:

Il campo dei quozienti Q(D) di un dominio d’integrità D è il più piccolo campo contenente D, nel senso che ogni altro campo K in cui D si immerge come sottoanello contiene un sottocampo isomorfo a Q(D); in questo senso il campo dei quozienti di un dominio è quindi unico. La costruzione del campo dei quozienti di un dominio d’integrità D rientra come caso particolare in una costruzione più generale (che si applica anche ad anelli che non sono integri), che va sotto il nome di → localizzazione.