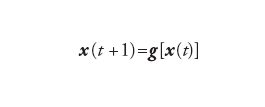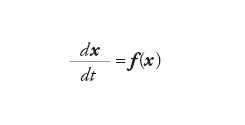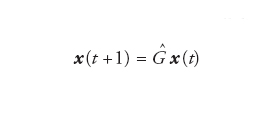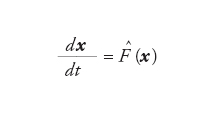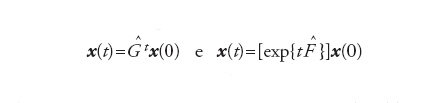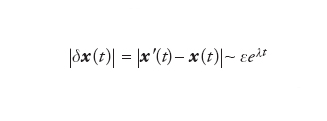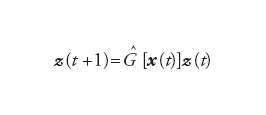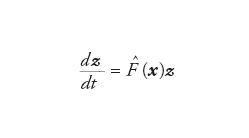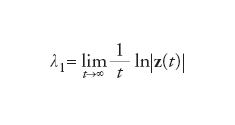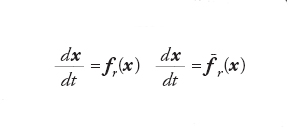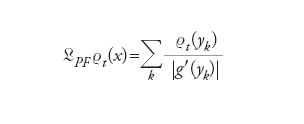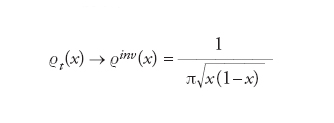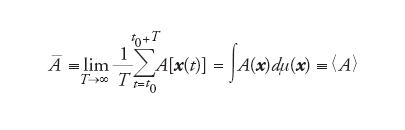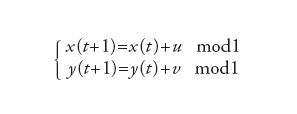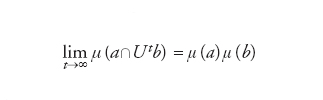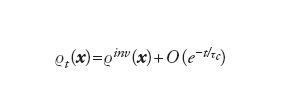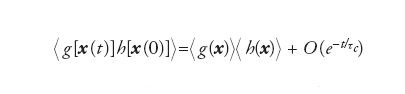Caos deterministico

Caos deterministico

Il programma di formalizzazione matematica della realtà inaugurato con la pubblicazione, nel 1687, dei Principia Mathematica di Isaac Newton è un punto di riferimento per tutte le teorie scientifiche. Ci si aspetta che, una volta scritte le equazioni differenziali che regolano l'evoluzione temporale di un fenomeno e determinate le condizioni iniziali, si possano risolvere le equazioni stesse e pervenire a una completa conoscenza del sistema, per ogni istante di tempo successivo. Esempi di sistemi per i quali tale programma può essere attuato sono il moto dei corpi celesti sotto l'azione della forza di gravità e le oscillazioni periodiche di un pendolo. Non in tutti i sistemi fisici e non per tutte le condizioni iniziali, ovviamente, la situazione è abbastanza semplice da poter essere risolta con soddisfazione; tuttavia, non vi è nulla che, in linea di principio, contrasti con l'idea che le equazioni del moto possano essere risolte mediante calcoli più o meno complessi.

Il cosiddetto problema dei due corpi, di cui è un esempio lo studio del moto di un pianeta intorno al Sole condotto trascurando la piccola interazione con gli altri pianeti e risolvendo le equazioni differenziali basate sulla legge di gravità, è abbastanza semplice da affrontare. Decisamente più complicato risulta invece il problema dei tre corpi, per esempio Sole, Terra e Luna, oppure Sole, Giove e un asteroide: per lungo tempo l'indagine del fenomeno non è stata approfondita, in quanto si riteneva che le difficoltà che si presentavano dipendessero esclusivamente dalla tecnica risolutiva. Verso la fine del XIX sec., il problema fu compreso dal matematico francese Henri Poincaré, il quale dimostrò che esso non ammette soluzioni approssimate valide per un tempo arbitrariamente grande e per tutte le condizioni iniziali. Una simile peculiarità si deve al fatto che nel problema dei tre corpi devono necessariamente presentarsi traiettorie dal comportamento che oggi definiamo caotico, caratterizzato cioè da una forte dipendenza dalle condizioni iniziali: se lo stato di partenza di un sistema con tali proprietà è modificato anche di poco, si possono produrre effetti molto rilevanti nello stato di arrivo. Esistono interessanti conferme sperimentali del ruolo del caos in ambito astonomico, per esempio negli asteroidi che orbitano intorno al Sole, negli anelli di Saturno e nel sistema di tre corpi costituito da Saturno, Titano e Iperione; in quest'ultimo caso, una conferma indiretta è stata fornita dalle immagini inviate dal satellite Voyager.

A partire dagli anni Sessanta del XX sec., il comportamento caotico è stato riscontrato in differenti sistemi fisici: sistemi ottici (per es. il laser) e allo stato solido (semiconduttori), plasmi, macchine acceleratrici, circuiti elettrici non linerari, sistemi acustici, oceani, atmosfera. Lo studio del caos deterministico, oltre alla sua rilevanza squisitamente tecnica, ha contribuito a produrre un ripensamento critico della dicotomia esistente tra determinismo e probabilità, evidenziando come in particolari situazioni molti fenomeni naturali, pur essendo descritti da leggi deterministiche, manifestano comportamenti predicibili, eventualmente, in senso soltanto probabilistico.

Concetti elementari

Un sistema dinamico è definito formalmente da: (a) uno spazio delle fasi Ω, costituito dai possibili stati del sistema; (b) una legge di evoluzione temporale deterministica che, dato lo stato del sistema al tempo t = 0, specificato dal vettore x(0)∈Ω, determina lo stato x(t) al tempo t  in modo univoco, vale a dire: x(0)→x(t)=U^tx(0); (c) una misura di probabilità dμ(x), invariante sotto l'evoluzione temporale: μ(A)=μ(U ^−tA), dove A è un insieme appartenente a Ω e U^−t è l'insieme dei punti che si trovano in A dopo un tempo t. Le più comuni leggi di evoluzione deterministiche sono le mappe e le equazioni differenziali; nel primo caso il tempo assume valori discreti:

[1] formula

nel secondo caso la legge di evoluzione è

[2] formula

Per le mappe il determinismo è ben evidente: dato x(0), la [1] permette di calcolare x(1) e, iterando il procedimento, x(2), x(3),…, fino a ottenere x(t).

Per le equazioni differenziali, il determinismo è una conseguenza del teorema, valido sotto ipotesi molto generali, di esistenza e unicità delle soluzioni.

I più semplici sistemi dinamici sono quelli lineari, ossia:

[1′] formula[2′]

dove Ĝ F ̂sono matrici i cui elementi sono costanti nel tempo. In casi come questi, è immediato determinare la soluzione a ogni tempo t, del tipo

[3] formula

sebbene si possano ottenere soltanto soluzioni piuttosto semplici: rilassamento verso soluzioni stazionarie, oppure moti (quasi) periodici.

fig.1

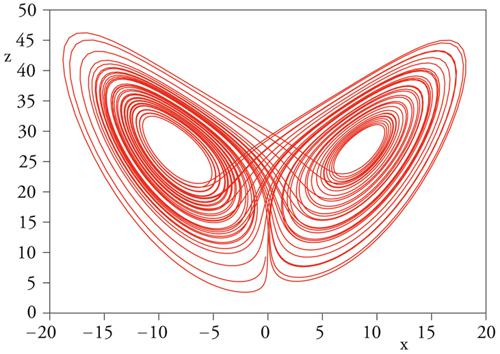
Nei sistemi non lineari, a parte casi eccezionali come i sistemi integrabili, non è possibile trovare le soluzioni e, inoltre, si possono avere comportamenti non banali, per esempio moti aperiodici e caos deterministico (fig.1). Indipendentemente dalla difficoltà di pervenire alla soluzione esplicita, è possibile classificare almeno qualitativamente il comportamento di un sistema dinamico, in base alla natura del suo attrattore e al valore degli esponenti di Ljapunov. L'attrattore è il luogo dei punti dello spazio delle fasi percorsi da una traiettoria dopo un transiente sufficientemente lungo e gode dell'importante proprietà che, se un punto x(0) appartiene a esso, allora vi appartiene anche x(t)=U^tx(0); vale a dire che l'attrattore è invariante per evoluzione temporale.

Nei sistemi dinamici che hanno un attrattore, detti dissipativi, il volume nello spazio delle fasi si contrae nel tempo; nel caso di equazioni differenziali, questa proprietà è verificata se ∑_i∂f_i/∂x_i〈0.

Analogamente, una mappa è detta dissipativa se ∣detG∣〈1, dove gli elementi della matrice G sono G_ij = ∂g_i/∂x_j. La contrazione del volume nello spazio delle fasi è abbastanza comune, anche se esiste una eccezione notevole costituita dai sistemi meccanici privi di attrito, detti hamiltoniani.

L'esempio più semplice di attrattore è il punto fisso asintoticamente stabile, tale che, se lo stato del sistema all'istante iniziale x(0) non è molto lontano dal punto fisso x*, x(t) si avvicina molto rapidamente a x*. La stabilità di un punto fisso può essere determinata, analogamente al caso dei sistemi lineari, studiando gli autovalori della matrice G_ij, nel caso delle mappe, e della matrice F_ij=∂f_i/∂x_j, per le equazioni differenziali, le derivate essendo calcolate nel punto fisso x*.

Un esempio familiare di punto fisso asintoticamente stabile è fornito dal pendolo con attrito, il cui attrattore è costituito dal solo punto fisso. L'attrattore più semplice dopo il punto fisso è il ciclo limite: la traiettoria si avvicina velocemente a una curva chiusa (ciclo) e quindi, dopo un transiente, si ha un moto pressoché periodico. Un esempio di ciclo limite è dato dall'oscillatore di van der Pol, che descrive un circuito elettrico non lineare che soddisfi l'equazione d2/dt2−ε(1−x²)dx/dt+x=0: se ε〈0, si ha un punto fisso stabile in (x=0; dx/dt=0), mentre se ε>0 il punto fisso diventa instabile e la traiettoria è attratta da un ciclo limite, approssimativamente una circonferenza nel piano (x, dx/dt). Oscillazioni periodiche (o quasi-periodiche) con N frequenze corrispondono al moto su un toro di dimensione N.

Caos deterministico e attrattori strani

Nei sistemi non lineari è possibile che si presentino comportamenti molto irregolari e che si verifichi il fenomeno della forte sensibilità alle condizioni iniziali. Questa proprietà può essere mostrata esplicitamente nella mappa logistica:

[4] x(t +1) = rx(t)[1− x(t)].

Con il cambiamento di variabile x(t)=[1−cos2πθ(t)]/2, per r=4 si ottiene

[5]  formula

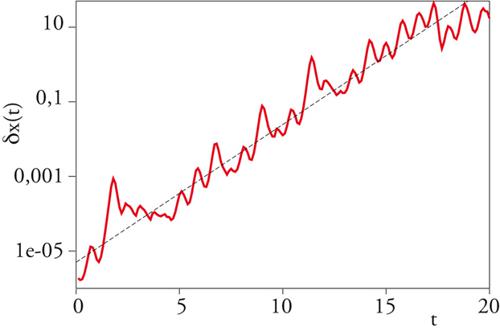
Date le condizioni iniziali θ(0) e θ′(0), che differiscono di una quantità molto piccola δθ(0), è facile calcolare δθ(t)=θ(t)−θ′(t), dove θ(t) e θ′(t) sono ottenute iterando la [5] a partire da θ(0) e θ′(0), ossia: δθ(t)=±2^tδθ(0). Si dice che un sistema dinamico deterministico è caotico se mostra una sensibile dipendenza dalle condizioni iniziali, ossia se due traiettorie x(t) e x′(t) inizialmente vicine si allontanano esponenzialmente:

[6]  formula

fig. 2

dove ε=∣x(0)−x′(0)∣ è piccolo e λ è l'esponente caratteristico di Ljapunov per il sistema; nel caso del sistema [5] è, ovviamenente, λ=ln2. Se si vuole predire lo stato del sistema con una tolleranza δ (fig. 2), non è possibile andare oltre il tempo di predicibilità T_p:

[7] formula

In linea di principio, T_p può essere aumentato a piacere diminuendo ε, ma, a causa della debole dipendenza, logaritmica, il tempo di predicibilità è determinato essenziamente da λ. Nei sistemi con una forte sensibilità alle condizioni iniziali, dopo un tempo T_p∼c/λ (dove c dipende, seppure poco, dalle condizioni iniziali) non ha più senso parlare di previsioni dello stato del sistema. Al contrario, nei sistemi lineari, non caotici, in cui si ha una debole dipendenza dalle condizioni iniziali, l'incertezza sullo stato iniziale non comporta gravi conseguenze sulle previsioni.

Esiste un'interessante conferma sperimentale del ruolo del caos in ambito astronomico. Gli asteroidi che orbitano intorno al Sole sono soggetti a una sollecitazione periodica causata dalla presenza di Giove. Se il periodo di rivoluzione dell'asteroide non è in rapporto razionale con quello di Giove, l'asteroide non è molto disturbato dalla perturbazione; in caso contrario si verificano effetti di risonanza che, accumulandosi velocemente, ne causano l'allontanamento dall'orbita imperturbata. Poiché il numero degli asteroidi è molto elevato, è possibile misurare la distribuzione di probabilità dei loro periodi, che evidenzia chiaramente la presenza di 'buchi' in corrispondenza di rapporti razionali semplici. Lo stesso tipo di fenomeno si ha con gli anelli di Saturno: in questo caso le lune del pianeta sono all'origine delle risonanze che provocano le note fasce nere, corrispondenti appunto ai periodi risonanti.

Il caos è presente anche nel sistema di tre corpi costituito da Saturno, Titano e Iperione; quest'ultimo ha una massa molto piccola rispetto a quella di Titano, e si presenta quindi una situazione analoga a quella del problema dell'asteroide in intererazione con Giove e il Sole (in questo caso Iperione, Titano e Saturno hanno rispettivamente il ruolo dell'asteroide, di Giove e del Sole). Questo sistema è in situazione risonante (ogni quattro rivoluzioni di Titano se ne hanno tre di Iperione) ed è stato mostrato che Iperione si trova sull'orlo di una zona caotica. I tempi in cui il caos si manifesta sono molto lunghi e quindi non è possibile osservare direttamente un comportamento irregolare nel moto di Iperione, tuttavia una conferma indiretta è stata fornita dalle immagini inviate dal satellite Voyager. In presenza di caos, eventuali frammenti staccatisi da Iperione (per es. in seguito a urti con altri frammenti oppure per effetti di marea) a causa della forte dipendenza dalle condizioni iniziali dovrebbero allontanarsi velocemente, disperdendosi nello spazio; è quindi naturale attendersi che Iperione sia di forma molto irregolare. Quello che il Voyager ha fotografato è proprio un corpo con l'aspetto di una patata bitorsoluta in luogo dell'usuale sferoide.

Un altro esempio di quanto sia rilevante il caos deterministico si ha nel caso delle previsioni atmosferiche: anche ricorrendo a un rilevamento da satellite dello stato iniziale, a un modello matematico e ad algoritmi di integrazione molto accurati, non si potrà andare oltre un tempo dell'ordine di c/λ, dove λ dipende dalle proprietà della dinamica dell'atmosfera; in una stima realistica, 1/λ vale circa dieci giorni.

Se il moto non è caotico, il corrispondente attrattore è detto regolare: può essere un punto, una curva chiusa, una superficie o una ipersuperficie. Al contrario, in un sistema con forte dipendenza dalle condizioni iniziali si ha un attrattore che non è regolare, ma ha una struttura generalmente molto complicata, tipicamente di natura frattale. In questo caso, si parla di attrattore caotico o, nella terminologia introdotta da David Ruelle, di attrattore strano.

Oltre all'esponente λ discusso precedentemente, è possibile definire altri esponenti di Ljapunov λ_i. Consideriamo un sistema dissipativo in d dimensioni: una sfera d-dimensionale, che abbia centro in x(0), appartenga all'attrattore e abbia raggio ε molto piccolo, si deforma, durante l'evoluzione temporale, in un'ellisse il cui volume diminuisce nel tempo. Se al tempo t  l'ellisse ha semiassi l_i(t), gli esponenti caratteristici di Ljapunov λ₁,λ₂,λ₃,…,λ_d (numerati in modo decrescente: λ₁≥λ₂≥λ₃…) sono definiti in modo tale che λ_i=(1/t)ln[l_i(t)/ε], dove t deve essere molto grande.

Per poter parlare di ellisse, nella precedente equazione è necessario prendere prima il limite per piccoli ε e poi quello per grandi t, in modo che l_i(t) non sia mai troppo grande. Il primo esponente λ₁ coincide con il λ introdotto nell'equazione [6].

Si possono formalizzare le precedenti definizioni introducendo il vettore tangente z(t) (corrispondente a una perturbazione infinitesima della traiettoria x(t)), che evolve, nel caso delle mappe [1], secondo la legge

[8] formula

dove gli elementi della matrice Ĝ  sono G_ij(x)=∂g_i(x)/∂x_j. Analogamente, nel caso di equazioni differenziali [2] si ha

[9] formula

dove gli elementi della matrice F̂ sono F_ij(x)=∂f_i(x)/∂x_j.. Un importante risultato matematico dovuto a Valery I. Oseledet dimostra che in sistemi ergodici è possibile definire in modo rigoroso tutti gli esponenti di Ljapunov: per esempio nel caso di λ₁, per quasi ogni scelta del vettore tangente z(0) si ha

[10] formula

Valgono le seguenti proprietà: (a) nei sistemi dissipativi si ha ∑_i λ_i〈0; (b) nei sistemi la cui evoluzione è data da un'equazione differenziale, se non vi sono punti fissi stabili, almeno un λ_i è nullo.

È possibile caratterizzare un attrattore per il tramite degli esponenti di Ljapunov: (a) per un punto fisso asintoticamente stabile tutti i λ_i sono negativi; (b) in un ciclo limite λ₁=0, λ_i〈0 per i>1; (c) nel moto su un toro N-dimensionale, λ₁=λ₂=…=λ_N=0 e λ_i〈0 per i>N; (d) in un sistema caotico, almeno un esponente di Ljapunov è positivo.

Gli esponenti di Ljapunov non soltanto caratterizzano un sistema dinamico da un punto di vista qualitativo, ma forniscono importanti informazioni su proprietà quantitative della dinamica caotica. Per esempio, la somma degli esponenti di Ljapunov positivi è uguale all'entropia di Kolmogorov-Sinai, o entropia metrica, con cui si può stimare il tasso di produzione di informazione del sistema.→∞

Transizione alla turbolenza

Uno dei maggiori successi della moderna teoria dei sistemi dinamici caotici è stata la spiegazione della transizione al caos, vale a dire il passaggio dal moto regolare a quello caotico al variare di un parametro di controllo r. Il caso forse più importante è quello della turbolenza fluidodinamica, in cui r è il numero di Reynolds.

Descriviamo brevemente i principali meccanismi per l'innesco della turbolenza, ossia i differenti scenari proposti da:

(a) Lev Davidovich Landau e Eberhard Friedrich Ferdinand Hopf;

(b) David Ruelle e Floris Takens;

(c) Mitchell Jay Feigenbaum;

(d) Yves Pomeau e Paul Manneville.

Nello schema di Landau e Hopf, il primo a essere proposto, il comportamento caotico è il risultato della sovrapposizione di un certo numero, crescente con r, di oscillazioni regolari di frequenza diversa. Ruelle e Takens hanno dimostrato che lo scenario di Landau e Hopf non può essere valido oltre la transizione da due a tre frequenze, in quanto la transizione da tre a quattro frequenze non è strutturalmente stabile, cioè non può avvenire nel caso di un sistema generico. Consideriamo due equazioni differenziali, l'una ottenuta modificando leggermente l'altra:

[11] formula

dove f̃_r(x) è vicina a f_r(x) nel senso che f̃_r(x) = f_r(x) + δf_r(x), con δf_r(x) piccolo. Ruelle e Takens hanno mostrato che, anche nel caso in cui il sistema descritto da dx/dt=f_r(x) evidenzi una transizione al caos attraverso il meccanismo di Landau e Hopf, questo stesso meccanismo non può intervenire nel sistema modificato, eccetto che per particolarissime scelte di δf_r(x). Si tratta di un risultato di grande importanza concettuale, il primo esempio di applicazione della moderna teoria dei sistemi dinamici caotici a fenomeni naturali. Non potendo infatti mai conoscere con precisione assoluta le vere equazioni di un fenomeno, non è sensato proporre un meccanismo che in genere scompare non appena le leggi del moto siano leggermente modificate. Nello scenario di Ruelle e Takens, rimangono della teoria di Landau e Hopf soltanto i primi tre passaggi: la transizione da punto fisso a ciclo limite per r=r₁, da ciclo limite a traiettoria con due frequenze per r =r₂, da traiettoria con due frequenze a traiettoria con tre frequenze per r =r₃; per r >r₄ si ipotizza il passaggio da una traiettoria con tre frequenze a moto caotico con un attrattore strano. È importante evidenziare che, mentre lo scenario di Landau e Hopf richiede un gran numero di gradi di libertà, quello di Ruelle e Takens ammette il caos anche nel caso di un'equazione differenziale con tre gradi di libertà.

Nel meccanismo proposto da Feigenbaum, si ha una successione di transizioni di raddoppio del periodo per determinati valori r₁,r₂,…,r_n del parametro di controllo; per valori di r  leggermente superiori a r_c=lim_n→∞r_n si ha caos. La successione r₁,r₂,…,r_n gode della notevole proprietà per cui lim_n→∞(r_n−r_n-1)/(r_n+1−r_n)= δ=4,6692… e il valore di δ non dipende dai dettagli della dinamica.

Come conseguenza, il diagramma di biforcazione della mappa ha una struttura autosimilare ad albero, con un raddoppio del numero di rami al passaggio per ogni valore r_n. Questo accade per ogni mappa unidimensionale della forma x_t+1=g_r(x_t), in cui la funzione g_r(x) ha un solo massimo di tipo quadratico e, perciò, intorno a esso può essere approssimata mediante una parabola. L'esistenza, per una vasta classe di leggi di evoluzione, di un meccanismo universale di transizione al caos, indipendente dalla forma dettagliata della funzione g_r(x), è particolarmente rilevante per le sue analogie con le transizioni di fase.

Un quarto scenario per la transizione al caos, introdotto da Pomeau e Manneville, nasce dall'osservazione del comportamento, detto intermittente, presente in alcuni fenomeni in chimica e in fluidodinamica. Se il parametro di controllo è leggermente più grande di un valore critico r_c, l'evoluzione del sistema è regolare per lunghi intervalli di tempo ed è inframezzata da brevi intervalli in cui si manifesta un comportamento irregolare. Il meccanismo di transizione al caos è quindi il seguente: per r〈r_c si ha un comportamento regolare, mentre per r=r_c+ε, con ε piccolo e positivo, il comportamento del sistema è regolare per un lungo intervallo di tempo, cui segue una fase turbolenta e un nuovo, lungo intervallo regolare, che non sarà in genere della stessa durata del precedente. La durata media della fase laminare (regolare) cresce al diminuire di ε, in misura proporzionale a 1/(ε)^1/2. Gli scenari (b), (c) e (d) sono stati osservati sia nelle simulazioni numeriche sia mediante esperimenti di laboratorio e rappresentano i soli meccanismi generali attraverso i quali un ciclo limite può perdere stabilità; il meccanismo (a), invece, non è mai stato osservato.

Teoria statistica del caos

Poiché i sistemi caotici, anche se deterministici, hanno proprietà per molti aspetti simili a quelle dei processi intrinsecamente stocastici ‒ per esempio l'impredicibilità‒, è piuttosto naturale trattarli da un punto di vista probabilistico. In questo contesto, a un'incertezza sullo stato iniziale corrisponde una densità di probabilità ϱ₀(x). Per semplicità di notazione, discutiamo soltanto sistemi a tempo discreto, descritti dalla [1]. L'evoluzione della densità di probabilità sarà:

[12]  formula

dove è utilizzato l'operatore di Perron-Frobenius. Per le mappe in una dimensione si ha:

[13] formula

dove y_k sono punti tali che g(y_k)=x e g′ indica la derivata. La [12] ha validità generale, ma il comportamento di ϱ_t(x) dipende dalle caratteristiche del sistema deterministico, in particolare dalla sua eventuale caoticità. Per esempio, nel caso della mappa logistica [4], se r〈3 si ha un solo punto fisso stabile, in x*=0 se r〈1 e in x*=(1−1/r) se 1〈r〈3; a tempi lunghi, ϱ_t(x) si concentra sul punto fisso x*. Al contrario, nel caso caotico, per esempio quello in cui r=4, quando t→∞ si osserva una rapida convergenza verso una misura invariante:

[14] formula

indipendentemente dalla scelta iniziale ϱ₀(x).

Un sistema dinamico (Ω, Ut; dμ(x)) è detto ergodico se

[15] formula

dove x(t)=U^tx−t0(t₀) (nel caso di sistemi a tempo continuo la somma è rimpiazzata, ovviamente, da un integrale). In un sistema ergodico una traiettoria molto lunga fornisce le stesse informazioni della misura μ(x). Nei sistemi caotici dissipativi, la misura invariante è singolare rispetto alla misura di Lebesgue, e per questo motivo è stata utilizzata la dμ(x) invece della più comune ϱ^inv(x)dx, cui è possibile ricorrere nel caso in cui esista una densità.

L'ergodicità non è una proprietà molto stringente, in quanto può valere anche in sistemi con comportamento piuttosto semplice, come la rotazione sul toro:

[16] formula

In questo caso, la misura invariante è quella di Lebesgue: dμ(x)=dxdy. Se u/v è un numero razionale, il sistema [16] è periodico; se u/v è irrazionale, il moto è quasi-periodico ed ergodico. In tale sistema non si può avere il rilassamento della ϱ_t verso una densità invariante: partendo con una ϱ₀(x, y) localizzata intorno a (x̂ ŷ),  la ϱ_t(x, y) non è altro che la traslazione della densità iniziale intorno a (U^t x̃ U^t ŷ).

Introduciamo ora il concetto di sistema mescolante (mixing): un sistema dinamico (Ω, U^t, d μ(x)) è mescolante se, per ogni coppia di insiemi a,b∈Ω, si ha

[17]  formula

La precedente condizione ammette una semplice interpretazione fisica. Immaginiamo di porre in un bicchiere d'acqua una goccia d'inchiostro, localizzata inizialmente in una piccola regione: il sistema dinamico è mescolante se, dopo un certo tempo, le particelle saranno disperse omogeneamente, ossia se, in ogni regione, il loro numero sarà proporzionale al volume della regione stessa. La proprietà di essere mescolante è più forte dell'ergodicità: un sistema mescolante è sicuramente ergodico, ma non viceversa, come dimostra l'esempio [16]. Se assumiamo che esista una densità invariante dμ(x)=ϱ^inv(x)dx e che il sistema sia mescolante, si ha un rilassamento, caratterizzato da un tempo caratteristico τ_c, verso la misura invariante; per tempi lunghi si ha cioè:

[18]   formula

Il tempo caratteristico di rilassamento verso la misura invariante τ_c determina il comportamento asintotico delle funzioni di correlazioni temporali:

[19] formula

dove le medie sono da intendere rispetto alla misura invariante. Sia il concetto di ergodicità sia quello di sistema mescolante sono stati originariamente introdotti nell'ambito della meccanica statistica, rispettivamente da Ludwig Boltzmann (per connettere le medie calcolate mediante gli insiemi statistici con le medie temporali lungo la traiettoria) e da Josiah W. Gibbs (per i fenomeni irreversibili). Nel caso della meccanica statistica di un sistema di N particelle lo spazio delle fasi è costituito dalla superfice ad energia costante su cui si svolge il moto, x=(q₁,q₂,…,q_N; p₁,p₂,…,p_N) dove q_n e p_n sono le posizione e gli impulsi della n-esima particella, l'evoluzione U^t è determinata dalle equazioni di Hamilton e la misura invariante è quella microcanonica.

Bibliografia

Arnold, Vladimir I., Equations différentielles ordinaires, Moscou, Mir, 1974.

Bergé, Pierre - Pomeau, Yves - Vidal, Christian, L'ordre dans le chaos, Paris, Hermann, 1984.

Cercignani, Carlo, Ludwig Boltzmann: The man who trusted atoms, Oxford, Oxford University Press, 1998.

Guerra, Francesco, Reversibilità/Irreversibilità, in: Enciclopedia Einaudi, Torino, Einaudi, 1980, XI, pp. 1067-1106.

Milani, Andrea, Il moto dei pianeti: ordine o caos?, "L'astronomia", 65, 1991, pp. 35-42.

Ott, Edward, Chaos in dynamical systems, 2. ed., Cambridge, Cambridge University Press, 2002.