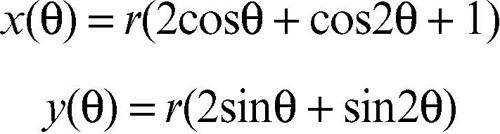cardioide

Enciclopedia della Matematica (2013)

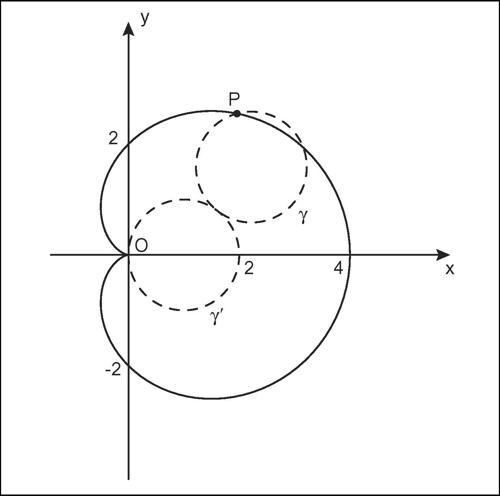
cardioide

cardioide curva piana epicicloide, a forma di cuore, definibile come il luogo descritto da un punto P fisso su una circonferenza γ che ruota, senza slittare, intorno a un’altra circonferenza γ′ di ugual raggio r. In coordinate polari e nella disposizione in figura, ha equazione ρ = 2r(1 + cosθ), in coordinate cartesiane (x ² + y ²)² − 4rx(x ² + y ²) − 4r ²y ² = 0. Le sue equazioni parametriche sono:

L’area della superficie racchiusa dalla cardioide è 6πr ², cioè sei volte l’area del cerchio generatore. La curva, nel sistema di riferimento scelto, è simmetrica rispetto all’asse delle ascisse e presenta una cuspide nell’origine. La cardioide è una lumaca di Pascal (→ Pascal, lumaca di), e in quanto tale appartiene alla famiglia delle concoidi.

cardioide

Enciclopedia on line

Curva algebrica piana ottenuta a partire da una circonferenza di raggio a (v. fig.) e dal fascio di rette passanti per un suo punto O, staccando su ciascuna retta segmenti 2a da ambo le parti delle ulteriori intersezioni con la circonferenza stessa: (x2 + y2)2 − 4ax (x2 + y2) − 4a2y2 = 0. La c. appartiene ...
cardioide

Dizionario delle Scienze Fisiche (1996)

cardiòide [Dal gr. kardioeidés "a forma di cuore"] [ALG] Curva algebrica piana: è il luogo descritto da un punto (P nella fig.) di una circonferenza c quando questa rotoli su un'altra circonferenza identica c', come dire la concoide, di intervallo pari al diametro a, di c' rispetto a un suo punto (O ...