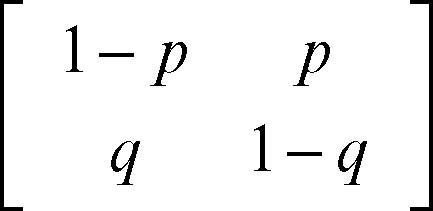Markov, catena di

Markov, catena di

Markov, catena di in probabilità, descrizione dell’evoluzione nel tempo di un sistema caratterizzato da un insieme discreto di stati in cui i cambiamenti di stato avvengono casualmente, secondo valori di probabilità e non in modo deterministico. Un sistema in evoluzione è infatti caratterizzato dagli stati che esso assume nel tempo: se il sistema è di tipo deterministico (noto con esattezza il dato iniziale è possibile determinare i dati successivi), allora è possibile prevedere con certezza il passaggio da uno stato all’altro in dipendenza di uno o più input prefissati, interni o esterni al sistema stesso. Se il passaggio da uno stato all’altro avviene con probabilità minore di uno, cioè diversa dalla certezza, allora il modello è di tipo probabilistico e una catena di Markov è in grado di darne una descrizione evolutiva nel tempo. Se le probabilità di passare da uno stato all’altro in un tempo unitario sono costanti e ogni stato dipende probabilisticamente soltanto dallo stato immediatamente precedente e non dalla complessiva “storia” del sistema, allora la catena di Markov è anche detta omogenea. Se il processo è continuo, anziché di catena si parla più propriamente di processo markoviano. Un esempio di catena di Markov è dato da un sistema che può esistere in un numero finito (o in un’infinità numerabile) di stati S_k e che in ogni istante t_h passa da uno stato S_i a uno stato S_j con probabilità p_ij indipendente dal particolare istante t_h considerato; un processo di questo tipo è completamente descritto dalla matrice delle probabilità di transizione e dalla distribuzione di probabilità all’istante considerato, detta matrice di transizione, in cui la somma dei valori di ognuna delle righe è uguale a 1. Per esempio, un sistema a due soli stati A e B può essere descritto dalla seguente matrice 2 × 2:

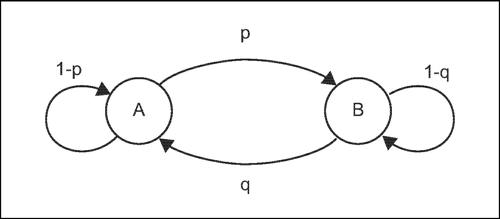
La descrizione dei passaggi di stato può avvenire anche mediante un grafo, detto grafo di transizione. In riferimento all’esempio precedente, ogni nodo rappresenta uno stato e gli archi di connessione indicano l’evoluzione del sistema da ogni stato a uno dei successivi possibili, con le rispettive probabilità. Le successive potenze di una matrice di transizione indicano le probabilità di passaggi tra stati in 2, 3, ..., n unità di tempo. Si dimostra che, se nella matrice di transizione non compaiono probabilità nulle, allora il limite della sua potenza ennesima, per n tendente all’infinito, è una matrice con tutte le righe uguali, le quali forniscono la probabilità che ha il sistema di trovarsi in ognuno degli stati indipendentemente dalla conoscenza degli stati precedenti.