cerchio dei nove punti
Enciclopedia della Matematica (2013)
cerchio dei nove punti
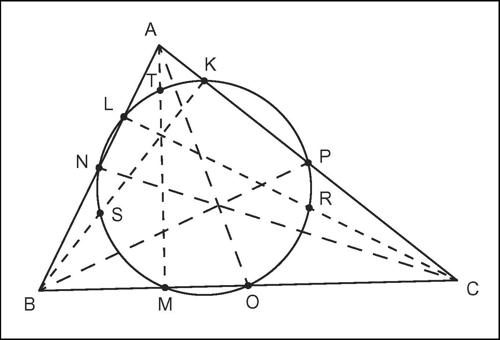
cerchio dei nove punti (detto anche cerchio di Eulero, ma noto anche come cerchio o circonferenza di Feuerbach) in un qualsiasi triangolo ABC, è così denominato il cerchio delimitato dalla circonferenza passante per i punti medi dei lati (N, O, P), per i piedi delle altezze (K, L, M), per i punti medi tra ciascun vertice e l’ortocentro (R, S, T). In un qualsiasi triangolo esiste sempre una e una sola circonferenza con queste caratteristiche. Il centro del cerchio di Eulero è detto centro dei nove punti.