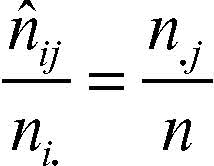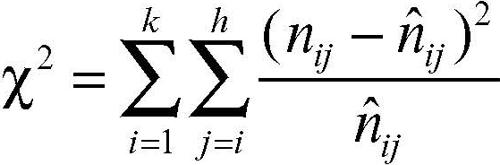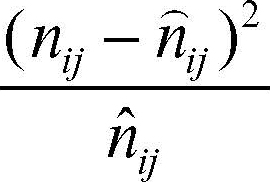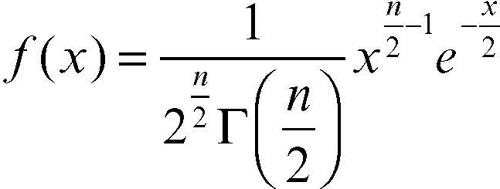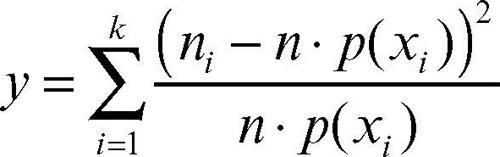chi-quadrato
chi-quadrato
chi-quadrato in statistica, numero indice (indicato con il simbolo χ2, cioè con la lettera greca «chi» al quadrato) detto anche indice di Pearson o di Pizzetti-Pearson; fornisce un criterio per stabilire se ci sia connessione o meno tra due caratteri statistici X e Y qualitativi, ponendo a confronto le frequenze osservate nelle distribuzioni dei due caratteri con le corrispondenti frequenze teoriche che si avrebbero nel caso di loro assoluta indipendenza.
Indicate con xi e yj (con i = 1, 2, ..., k e j = 1, 2, ..., h) le modalità rispettive di due caratteri X e Y, con nij la frequenza congiunta della coppia di modalità (xi, yj), si costruisce la seguente tabella a doppia entrata
in cui i numeri ni. indicano le frequenze marginali delle modalità del carattere X (in pratica i totali di riga) e i numeri n.j indicano le frequenze marginali del carattere Y (in pratica i totali di colonna). Se i due caratteri fossero indipendenti, allora, per ogni riga e colonna, sarebbero uguali i seguenti rapporti:
dove con n̂ij sono indicate le frequenze congiunte teoriche in caso di indipendenza. Pertanto, le frequenze congiunte teoriche in caso di indipendenza sono date da:
(totale di riga per totale di colonna diviso totale generale). L’indice del chi-quadrato stima la distanza della distribuzione di frequenza osservata dalla distribuzione di frequenza teorica che si avrebbe in caso di indipendenza fra i due caratteri ed è quindi:
dove nij sono le frequenze osservate dei caratteri congiunti.
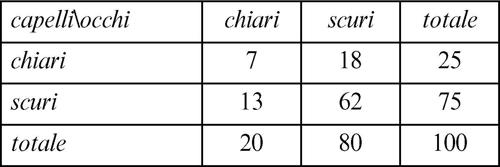
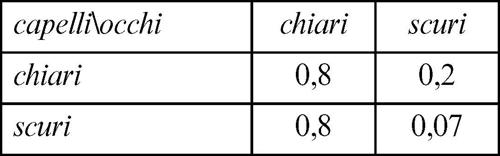
A titolo di esempio, si supponga di voler sapere se il carattere X = «colore degli occhi» e il carattere Y = «colore dei capelli», per ognuno dei quali si siano individuate, per semplicità, le modalità «chiaro» e «scuro», siano tra loro in qualche modo connessi e si supponga che, effettuata una rilevazione di tali caratteri in una popolazione di n = 100 persone, ci si trovi di fronte ai dati presentati nella seguente tabella a doppia entrata:
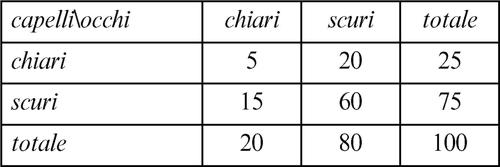
Si costruisce allora la tabella dei valori n̂ij delle frequenze congiunte teoriche in caso di indipendenza
e quindi la tabella dei valori che, per ogni frequenza congiunta, indicano la distanza relativa da quella teorica in base alla seguente formula:
Calcolando la somma si ottiene χ2 = 0,8 + 0,2 + 0,8 + 0,07 = 1,87.
L’indice χ2 assume valore 0 nel caso di indipendenza assoluta, mentre il suo valore massimo dipende dalla numerosità n della popolazione cui si riferisce. A partire dall’indice χ2 si costruiscono altri indici quali l’indice di → contingenza quadratica media (che mette in relazione l’indice con il totale n delle unità osservate) e l’indice di contingenza di → Cramér, che, variando da 0 a 1, ne costituisce una normalizzazione. Il χ2, che è un indice base utilizzato per valutare forme di connessione e dipendenza statistica soprattutto tra caratteri qualitativi, non fornisce informazioni significative se alcune frequenze congiunte (le caselle della tabella) presentano poche unità (inferiori a 5).
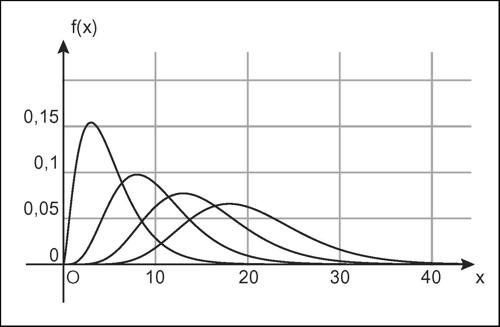
Chi-quadrato è a sua volta una variabile aleatoria continua, determinata completamente da un solo parametro: il numero n dei gradi di libertà. Essa si ottiene come somma dei quadrati di n variabili aleatorie indipendenti normali e standardizzate (quindi con media nulla e varianza uguale a 1). Perciò, date n variabili normali standardizzate zi, la variabile:
si distribuisce secondo la distribuzione chi-quadrato, la cui funzione di densità ƒ(x) è nulla per ogni x ≤ 0 e, per un dato valore intero positivo di n, è:
in cui Γ è la funzione gamma di Eulero. Il suo valore medio è n e la sua varianza 2n. Il grafico della funzione di densità è asimmetrico e la sua forma cambia a seconda del numero n dei gradi di libertà. Al crescere di n tende a una distribuzione normale. In statistica inferenziale, i test del chi-quadrato sono i test di verifica delle ipotesi che si basano su una variabile aleatoria che abbia distribuzione chi-quadrato. Se si vuole verificare l’ipotesi che, estratto un campione casuale di dimensione n, la distribuzione di un suo carattere con modalità {x1, ..., xk} si adatti a una variabile aleatoria X, con distribuzione di probabilità p(xi), si calcola:
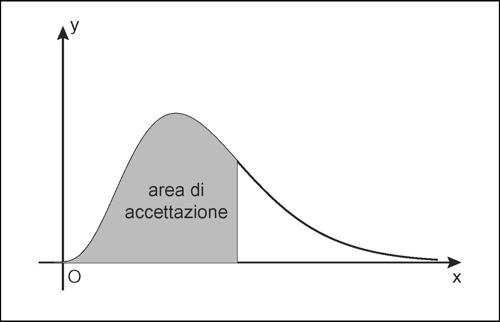
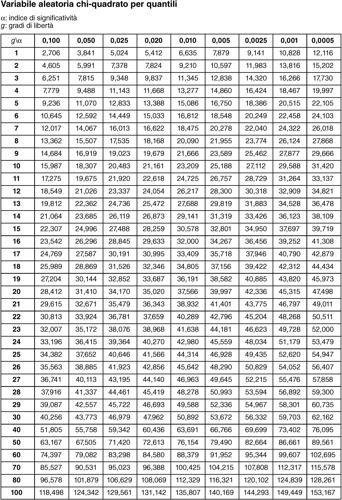
in cui gli ni indicano le frequenze delle modalità xi nel campione. Se n è sufficientemente grande (si assume come regola empirica che, per ogni i, n · p(xi) > 5), allora y ha approssimativamente una distribuzione chi-quadrato con k − 1 gradi di libertà. Usando un dato livello di significatività α, si confronta il valore ottenuto con quello che si legge nella tavola di distribuzione di χ2. Si accetta l’ipotesi nulla «p è la distribuzione di probabilità di X con probabilità superiore a 1 − α» se y < χ2k−1,1−α, altrimenti la si rifiuta. Si veda la tabella di distribuzione del chi-quadrato: in ogni casella sono riportati valori di χ2 con g gradi di libertà per i valori di probabilità 1 − α più utilizzati.