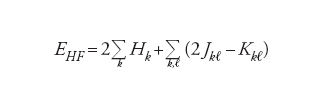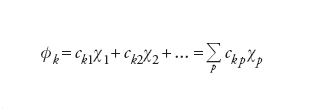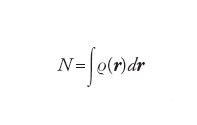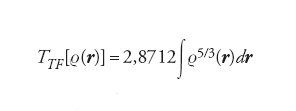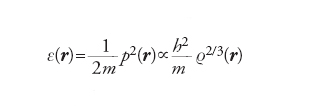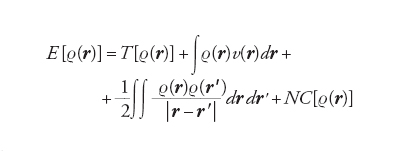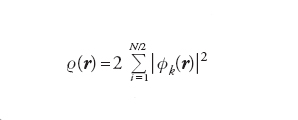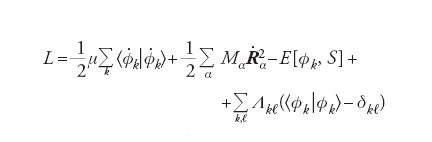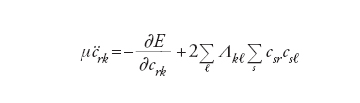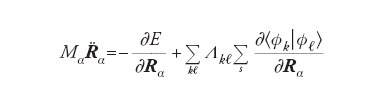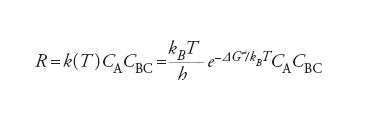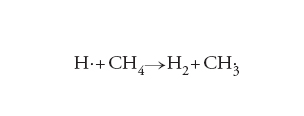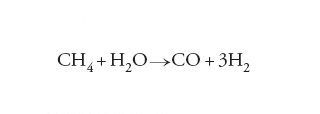Chimica computazionale

Chimica computazionale

La prospettiva di poter descrivere i fenomeni chimici mediante calcoli è affiorata, in termini concreti, nella prima metà del Novecento con l'avvento della meccanica quantistica. Infatti, dopo essere passata attraverso una fase di definizione concettuale, che ha ridisegnato il volto della chimica, ormai la meccanica quantistica è entrata in una fase operativa tale da essere in grado di valutare con accuratezza la struttura e l'energia delle molecole, sia quando sono isolate, sia quando collidono per dare origine a nuovi composti. Il riconoscimento del grande progresso così conseguito è testimoniato dall'attribuzione, nel 1998, del premio Nobel per la chimica a due scienziati, Walther Kohn e John A. Pople, per le loro ricerche sulla teoria del funzionale della densità e per lo sviluppo di metodi computazionali. Anche se l'approccio computazionale può sembrare troppo illuministico, in quanto sembra intaccare il tradizionale carattere sperimentale della chimica, esso, in realtà, sta acquistando un ruolo sempre più rilevante anche in numerosi settori scientifici e tecnologici connessi con questa scienza.

Infatti, se fino a qualche anno fa i chimici teorici si dovevano accontentare di riprodurre dati sperimentali già noti, attualmente essi possono avventurarsi ‒ seppure con cautela ‒ nella previsione di dati utili per orientare le indagini nei casi in cui le informazioni sperimentali dettagliate siano carenti. In particolare queste possibilità si verificano in campi come quello delle sintesi chimiche, dei processi di combustione, della catalisi, della chimica ambientale e atmosferica, della preparazione di materiali tecnologicamente avanzati, della biologia molecolare, della chimica cosmica e di altri ancora. La sinergia fra risultati sperimentali sempre più accurati riguardo la struttura e la dinamica delle molecole, e la loro interpretazione mediante dettagliati calcoli teorici, sta conferendo alla chimica un rinnovato slancio, non solo sul piano concettuale, ma anche nelle applicazioni su tematiche di frontiera.

È interessante osservare come la prospettiva di sviluppo di una concreta chimica computazionale fosse già stata preconizzata da Paul Adrien Maurice Dirac, uno dei padri della meccanica quantistica, quando nel 1929 affermava che "le leggi fisiche fondamentali necessarie per la teoria matematica dell'intera chimica sono ormai completamente note, e la difficoltà è dovuta solo al fatto che la loro applicazione porta a equazioni troppo complicate per essere solubili". Secondo Pople, l'esame retrospettivo della frase precedente appare "come un grido di trionfo e di disperazione", poiché essa preannunciava l'avvento di un colossale sforzo matematico. In questo senso la chimica computazionale si può allora considerare come la realizzazione ‒ in parte conseguita ma ancora in via di svolgimento ‒ del programma implicitamente enunciato da Dirac.

In realtà, la rilevanza che sta acquistando la chimica computazionale trae vantaggio anche dallo sviluppo di metodologie e tecniche sperimentali che permettono di ottenere informazioni sempre più accurate sulla struttura delle molecole, sulle transizioni energetiche cui sono soggette e sulla dinamica dei loro movimenti derivanti dalle interazioni con le altre molecole. In questo quadro meritano di essere menzionati i risultati ottenuti mediante l'impiego dei laser, che grazie alla produzione di impulsi dell'ordine dei femtosecondi permettono di cogliere le caratteristiche geometriche e dinamiche dei complessi molecolari che si formano all'atto di collisione dei reagenti stessi.

Il campo autoconsistente di Hartree-Fock

Il procedimento applicato per valutare l'energia di un sistema molecolare, costituito da un insieme di nuclei attorno ai quali gravitano gli elettroni, è quello definito del campo autoconsistente (SCF, Self-consistent field), nel quale il moto di ciascun elettrone viene descritto mediante opportune funzioni d'onda ϕ chiamate orbitali molecolari. Il quadrato di ϕ esprime la probabilità di trovare l'elettrone in un punto dello spazio. Per una molecola con un numero N pari di elettroni ‒ e pertanto dotata di una configurazione detta a guscio chiuso (closed shell) ‒ ciascun orbitale è occupato da 2 elettroni con spin antiparallelo. Il calcolo dell'energia viene condotto mediante la seguente espressione:

[1] formula[2]

La precedente relazione trova una giustificazione nel fatto che, in prossimità di ciascun nucleo, l'elettrone risulta essenzialmente soggetto al campo di forza di quest'ultimo e pertanto il suo comportamento è descritto dal corrispondente orbitale atomico.

La ricerca della migliore serie dei coefficienti c_kp viene perseguita applicando il principio variazionale, in base al quale i valori delle energie corrispondenti a funzioni d'onda approssimate sono superiori o, al limite, uguali all'energia E₀ dello stato fondamentale del sistema. Questo problema è stato affrontato e risolto nel 1951 da Clemens C. J. Roothaan, il quale ha dimostrato che la ricerca del valore minimo dell'energia viene ricondotta alla soluzione di un sistema di equazioni algebriche non lineari, solitamente perseguita per via numerica mediante il procedimento iterativo. Il metodo, indicato con l'acronimo LCAO-SCF (Linear combination of atomic orbitals self-consistent field) è stato esteso anche ai sistemi a guscio aperto, nei quali, cioè, alcuni orbitali sono occupati da 1 solo elettrone anziché da 2. In tal modo il metodo può essere applicato anche alle specie chimiche contenenti 1 elettrone spaiato. L'insieme degli orbitali atomici impiegati, centrati su ciascun nucleo atomico, viene chiamato serie di funzioni di base (basis set) e i calcoli così eseguiti vengono denominati ab initio.

fig. 2

Essi sono utilizzati per valutare le interazioni fra gli elettroni, espresse sotto forma di integrali la cui soluzione risulta poco agevole, soprattutto quando gli orbitali atomici in gioco sono centrati su 3 o 4 atomi. Questa difficoltà ha provocato un rallentamento del programma della chimica quantistica, creando fra i ricercatori un clima di sconforto dovuto al cosiddetto incubo degli integrali. La situazione si è protratta per alcuni anni, sino a quando si è affermata la tendenza a utilizzare orbitali atomici espressi da funzioni gaussiane, per i quali il calcolo degli integrali risulta molto più agevole e perseguibile per via analitica. Questo approccio è maturato negli ultimi vent'anni del XX sec., grazie allo sviluppo del calcolo elettronico, attraverso la formulazione di programmi mediante i quali è ormai possibile valutare l'energia molecolare con un'ottima approssimazione. Tale accuratezza permette di affrontare anche problemi concernenti il calcolo dei parametri che caratterizzano la velocità delle reazioni chimiche, ottenendo risultati confrontabili con quelli sperimentali (fig. 2). Per rendersi conto dell'impegno di calcolo numerico richiesto, è sufficiente osservare che il numero degli integrali di interazione elettronica coinvolti è all'incirca proporzionale a N⁴, dove N è il numero di funzioni atomiche impiegate. Il metodo permette di determinare le configurazioni geometriche delle molecole, ricercando il minimo della loro energia in funzione delle distanze e degli angoli di legame.

2. Ruolo della correlazione elettronica

Nel metodo del campo autoconsistente, il moto di ciascun elettrone viene influenzato da quello degli altri solo attraverso un campo medio, ignorando il fatto che la repulsione elettrostatica istantanea dà origine a una correlazione nel moto di ciascuna coppia di elettroni, poiché essa riduce significativamente la probabilità di trovare un elettrone in prossimità di un altro. Questo effetto potrebbe essere attribuito alla presenza di una cavità detta di Coulomb con dimensioni tipiche dell'ordine dell'Ångstrom. La correlazione influisce sui valori dell'energia associata a una coppia di elettroni di legame per circa 25 kcal/mole, quindi dello stesso ordine di grandezza dell'energia di legame. L'energia totale di una molecola viene riferita a quella delle particelle separate, ovvero i nuclei e gli elettroni. Per esempio, per l'acqua il valore sperimentale dell'energia, sottratta quella relativistica (stimata −0,045 a.u.), ammonta a −76,438 ±0,003 a.u., di cui −0,370 a.u. (232,18 kcal/mole) corrispondono all'energia di correlazione. Anche se l'energia di correlazione è relativamente piccola, essa gioca un ruolo importante nella simulazione dei processi di rottura e di formazione dei legami che intervengono nelle reazioni chimiche. Il calcolo dell'energia di correlazione, secondo Christian Moller e Milton S. Plesset, può essere ottenuto attraverso l'applicazione del metodo delle perturbazioni, che introduce una serie di termini correttivi ai risultati conseguiti con il metodo del campo autoconsistente. I diversi ordini del calcolo perturbativo vengono indicati con le sigle MP2, MP3 e così via. L'approccio è corretto, ma purtroppo la serie così ottenuta è lentamente convergente e presenta nel suo sviluppo espressioni algebriche sempre più complesse. Comunque, la sua applicazione permette di riprodurre i valori dell'energia di correlazione, con un'efficacia che dipende ovviamente dall'ordine cui si spinge lo sviluppo del calcolo.

3. Metodo del funzionale della densità

In due lavori pionieristici, pubblicati nel 1927 indipendentemente da Enrico Fermi e da Llewellyn H. Thomas, era applicato un approccio statistico per ottenere una descrizione ragionevolmente approssimata della distribuzione degli elettroni in un atomo polielettronico. La possibilità di applicare il metodo alle molecole è emersa nel 1964, quando Pierre Hohenberg e Walter Kohn hanno dimostrato che la funzione d'onda poteva essere sostituita dalla densità elettronica ϱ(r), che esprime il numero di elettroni presenti nell'unità di volume e soddisfa la relazione:

[3] formula

dove dr è un elemento di volume nell'intorno del punto definito dal vettore r. Nell'ambito dell'approssimazione di Thomas-Fermi, l'energia cinetica degli elettroni può essere espressa in funzione della densità come segue:

[4] formula

Infatti, se a un generico elettrone, situato in una posizione definita da r e avente quantità di moto p(r), si associa una cavità sferica di diametro a(r), la densità locale risulta espressa da ρ(r)=6/4πa³(r). Poiché, in virtù del principio di indeterminazione, p∼h/a, l’energia cinetica locale dell’elettrone sarà espressa dall’equazione:

[5] formula

L’energia totale, allora, si calcola integrando l’espressione e(r)r(r)dr, la quale, così ottenuta, non risulta però sufficientemente accurata per affrontare problemi di energetica molecolare.

Una prescrizione per produrre un numero da una funzione, che a sua volta dipende da più variabili, viene chiamata funzionale. Sia la funzione d’onda che la densità dipendono da r, mentre l’energia, che dipende dalla funzione d’onda, è un funzionale. Per evidenziarlo essa viene scritta nella forma e[r(r)], caratterizzando il funzionale con le parentesi quadre. Hohenberg e Kohn hanno dimostrato che l’energia dello stato fondamentale di un sistema di elettroni è un funzionale della densità elettronica che, in forma esatta, si può scrivere come segue:

[6] formula

dove T[ρ(r)] è l’energia cinetica e v(r) quella potenziale di interazione con i nuclei. L’energia potenziale è espressa dalla somma di due interazioni elettrostatiche classiche: la prima fra elettroni e nuclei; la seconda fra le due distribuzioni elettroniche ρ(r) e ρ(r '). Il termine NC [ρ(r)], definito non classico, contiene l’energia di scambio e di correlazione e risulta implicitamente definito dalla precedente equazione. Questo importante risultato ha portato alla formulazione del metodo del funzionale della densità (DFT, Density functional theory), che si può considerare una vera e propria innovazione nel panorama dell’energetica molecolare. Un efficace procedimento per applicarlo, suggerito dallo stesso Kohn e da Lu J. Sham, è basato sull’impiego di una serie di orbitali molecolari φ_k(r) relativi a un sistema di elettroni non interagenti, mediante i quali si valuta la densità elettronica nel modo seguente:

[7] formula

L’energia, allora, si esprime come somma dell’energia cinetica esatta degli elettroni non interagenti e dell’energia dovuta a un potenziale efficace che contiene, oltre ai termini coulombiani classici, anche l’energia di scambio e di correlazione, nonché una piccola correzione dovuta all’influenza della correlazione stessa sull’energia cinetica. I valori dei coefficienti degli orbitali – e quindi l’energia del sistema – si ottengono applicando il principio variazionale mediante un procedimento numerico iterativo, per cui il DFT richiama quello LCAOSCF, anche se la sua applicazione risulta più agevole e per certi versi più efficace. Il metodo, esatto nella sua impostazione, richiede però la valutazione del potenziale efficace attraverso opportune approssimazioni, tenendo conto che gli effetti di scambio e di correlazione riflettono un’azione di schermatura, poiché ciascun elettrone tende a escludere che gli altri gli si avvicinino.

fig. 3

Tale energia non classica può essere scritta come somma di due contributi relativi, rispettivamente, allo scambio e alla correlazione. Per calcolare il primo termine è stato individuato un approccio semplice chiamato approssimazione della densità locale o LDA (Local density approximation). Esso fa uso dei risultati ottenuti nello studio del comportamento di un gas elettronico distribuito in modo uniforme in una scatola, nella quale è presente un potenziale positivo e omogeneo tale da mantenere il sistema neutro. La valutazione del termine di correlazione viene condotta con metodi numerici, per esempio utilizzando la tecnica Monte Carlo. I risultati ottenuti sono stati successivamente interpolati in modo da poterli impiegare agevolmente nelle diverse applicazioni. Malgrado la semplicità delle ipotesi che stanno alla sua base, l’LDA fornisce risultati di soddisfacente accuratezza che, comunque, può essere migliorata tenendo conto che la densità elettronica non è omogenea, e introducendo quindi un’opportuna correzione, detta di non località. Un procedimento analogo è stato impiegato per valutare con maggior cura anche l’energia di correlazione. Esistono diverse varianti del DFT che differiscono soprattutto per la scelta delle funzioni atomiche di base. Attualmente esso costituisce un utile strumento per valutare le caratteristiche strutturali e dinamiche delle molecole. La sua applicazione permette di esplorare il comportamento di strutture molecolari di particolare interesse, comprese le nanostrutture (fig. 3).

Cinetica e dinamica  delle reazioni chimiche

Le trasformazioni chimiche coinvolgono diversi stadi elementari nei quali intervengono composti instabili e reattivi che, se pur presenti in piccola quantità, possono influenzare in modo significativo la velocità del processo globale. Per poter formulare modelli in grado di descrivere sia i processi naturali sia quelli di interesse applicativo, è necessario conoscere i parametri che caratterizzano le velocità delle reazioni coinvolte. Poiché la determinazione per via sperimentale delle velocità non è sempre agevole, risulta utile poter disporre di metodi di calcolo in grado di sopperire a tale esigenza. La rottura e la formazione di legami fra atomi, che hanno luogo in una reazione chimica, possono essere descritte su opportune superfici che rappresentano i valori dell’energia potenziale in funzione delle posizioni occupate dai diversi atomi presenti nelle molecole interagenti.

La superficie così ottenuta viene indicata con l’acronimo PES (Potential energy surface). Per una molecola non lineare costituita da n atomi è richiesto uno spazio di 3n ˗ 5 dimensioni, la qual cosa mette bene in evidenza la difficoltà di descrivere graficamente le PES. Malgrado questa limitazione, le PES si rivelano molto utili per lo studio dei meccanismi delle reazioni chimiche. Per esempio, nella reazione di sostituzione la PES, che descrive il passaggio dai prodotti ai reagenti con la rottura e la formazione dei corrispondenti legami, ha un tipico andamento che individua il percorso lungo il quale il valore locale dell’energia in ogni punto del cammino è minimo rispetto a spostamenti a esso perpendicolari. Il passaggio dai reagenti ai prodotti è condizionato dal superamento di una barriera di energia potenziale e la differenza E≠ fra le energie di punto zero del massimo e dei reagenti si identifica con l’energia di attivazione della reazione.

fig. 4

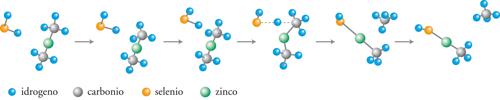
I recenti sviluppi della chimica computazionale offrono la possibilità di valutare in modo accurato le PES anche per reazioni relativamente complesse, aprendo così ampie prospettive nel panorama della cinetica chimica. La dinamica di una collisione può essere studiata descrivendo il moto del punto che rappresenta il sistema reagente sulla PES mediante la meccanica classica. Integrando numericamente le equazioni del moto si simulano le traiettorie descritte dal punto rappresentativo, compatibilmente con diverse condizioni iniziali che caratterizzano lo stato delle molecole reagenti, in particolare la loro posizione relativa e la loro energia. Quelle che superano la barriera di energia potenziale corrispondono a collisioni reattive, per cui l’esame di un numero ragionevolmente elevato di tali collisioni – campionate a caso per quanto concerne l’energia e l’orientazione relativa delle molecole – fornisce la probabilità che abbia luogo la reazione. In realtà i calcoli sono molto onerosi, per cui la loro applicazione rimane ancora limitata a sistemi molecolari semplici. Nella fig. 4 viene illustrata l’evoluzione di una delle reazioni coinvolte nel processo di sintesi di un materiale di interesse nell’optoelettronica, il seleniuro di zinco (ZnSe). Il cammino della reazione fra seleniuro di idrogeno e zinco dimetile è stato simulato valutando l’energia delle due molecole che entrano in collisione per diverse posizioni relative, incluse quelle corrispondenti allo stato di transizione. Il prodotto ottenuto (CH₃ZnSeH) interagisce successivamente con la superficie del solido depositando ZnSe.

Un metodo efficace è quello proposto da Roberto Car e Michele Parrinello, i quali dopo aver valutato con il DFT gli orbitali Φ_kl(r) del punto di inizio, li sviluppano in onde piane. Nella chimica quantistica questa scelta è inconsueta, mentre è comune nella fisica della materia condensata e offre alcuni vantaggi, fra i quali la facilità dei calcoli numerici. I coefficienti dello sviluppo c_rk vengono trattati come una serie di variabili dinamiche che evolvono in modo simultaneo alla variazione delle posizioni nucleari. Lo scopo viene conseguito introducendo una massa fittizia m opportunamente scelta – per esempio facendo in modo che la distribuzione degli elettroni sia prossima a quella della configurazione di Born-Oppenheimer. Dal punto di vista formale, si procede in accordo con la meccanica classica introducendo una lagrangiana espressa come segue:

[8]  formula

dove E[Φ_k, S] è l’energia del sistema riferita a una particolare configurazione nucleare, indicata collettivamente con S e calcolata mediante il DFT, mentre i punti indicano le derivate rispetto al tempo. Per semplicità, inoltre, è stata adottata la notazione di Dirac ∫Φ*_kΦ_ℓdr = [Φ_k /Φ_ℓ] mentre l’ultimo termine al secondo membro viene introdotto per imporre che gli orbitali soddisfino le condizioni di ortonormalità. Λ_kℓ sono i corrispondenti parametri di Lagrange.

In questa impostazione i gradi di libertà del sistema sono le coordinate nucleari R_α e i coefficienti c_rk degli orbitali. Lo studio del comportamento dinamico consegue dall’applicazione alla precedente delle equazioni di Eulero- Lagrange, da cui si ottiene:

[9]   formula[10]

L’integrazione delle equazioni precedenti, a partire da una configurazione iniziale, permette di ricavare la dipendenza dei crk e delle R_α dal tempo, e quindi di descrivere la dinamica di sistemi molecolari attraverso l’evoluzione della loro configurazione geometrica e della densità elettronica verso una situazione di equilibrio, caratterizzata da un valore minimo dell’energia. Il metodo è particolarmente adeguato per piccoli aggregati atomici e per studiare la struttura delle superfici. Più recentemente è stato applicato anche alla descrizione del comportamento dinamico di sistemi molecolari di rilevanza biologica.

Se si escludono reazioni molto veloci, è ragionevole assumere che esista una distribuzione di equilibrio fra i diversi moti molecolari interni, eccetto ovviamente quello lungo la coordinata di reazione. La velocità di reazione R, allora, viene valutata come flusso medio dei reagenti che attraversa la regione alla sommità della barriera e viene espressa dalla relazione seguente:

[11] formula

dove C_A e C_BC sono le concentrazioni dei reagenti e k_B la costante di Boltzmann. ΔG^≠ è la variazione di energia libera, detta energia di attivazione, associata al passaggio dai reagenti allo stato di transizione, ovvero a quel complesso molecolare instabile (complesso attivato) che si trova alla sommità della barriera di energia potenziale, in corrispondenza della configurazione [A…B…C]^≠, nella quale il legame A^_B non è ancora del tutto formato e quello B^_C non è completamente rotto. Malgrado la sua esistenza effimera (10^_12 :̶10^_11 s), le caratteristiche geometriche e le frequenze di vibrazione atomiche del complesso attivato si possono calcolare dall’andamento della PES nell’intorno della zona della sua esistenza. Utilizzando queste informazioni si risale al ΔG^≠ e quindi alla costante di velocità della reazione.

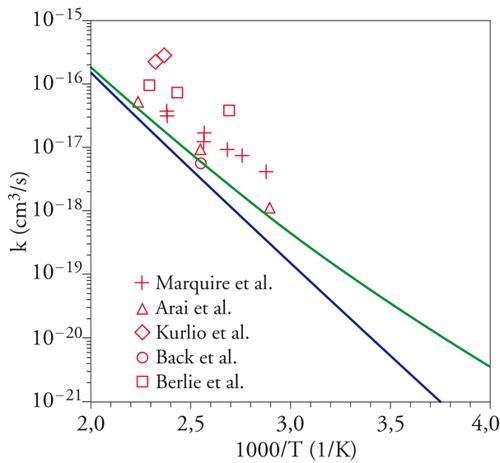
Nella letteratura si trovano diversi esempi in cui la chimica computazionale viene impiegata per delucidare il meccanismo delle reazioni chimiche. Di particolare interesse sono i risultati concernenti il calcolo della velocità di reazione, condotti sia con la dinamica molecolare  sia con la teoria dello stato di transizione o TST (Transition state theory). A questo proposito è interessante menzionare che per la reazione:

[12] formula

che interessa i processi di combustione, si sono ottenuti i risultati illustrati nella fig. 2, da cui appare che i dati calcolati sono confrontabili con quelli sperimentali.

fig. 5

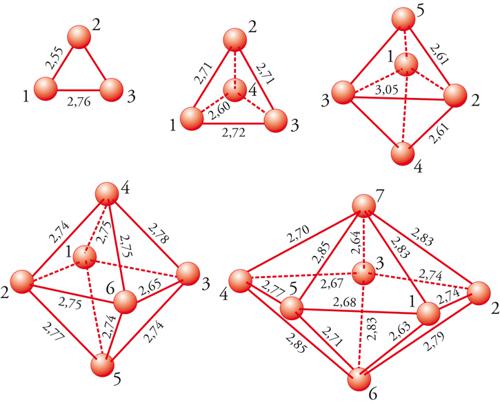
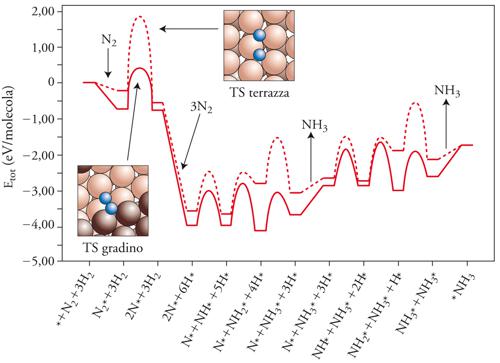
Di particolare interesse sono gli studi sulla catalisi eterogenea. Per esempio, la sintesi dell’ammoniaca coinvolge diversi stadi che riguardano l’adsorbimento dell’azoto e dell’idrogeno molecolari e le loro interazioni sulla superficie. I calcoli sono stati effettuati da Jens K. Mørskov su un catalizzatore costituito da una superficie monocristallina di rodio metallico, considerando due casi specifici nei quali la reazione avviene rispettivamente sulla faccia a terrazza del monocristallo o su un gradino. I cammini di reazione così ottenuti sono riportati nella fig. 5. Si può osservare che lo stadio di adsorbimento dissociativo dell’azoto, che costituisce quello limitante la velocità del processo globale, presenta un valore più basso dell’energia di attivazione per la reazione che coinvolge gli atomi di rodio del catalizzatore che fanno parte di siti attivi localizzati in corrispondenza dei gradini. Inoltre, l’energia di attivazione risulta molto sensibile all’ambiente locale, definito dagli atomi adsorbiti nell’intorno del centro su cui ha luogo la reazione, per cui la velocità globale di reazione dovrà essere valutata mediando opportunamente i valori della velocità sui diversi centri. I valori così ottenuti risultano in ragionevole accordo con i dati sperimentali.

Un altro esempio interessante riguarda la reazione di steam reforming del metano per produrre il gas di sintesi:

[13]  formula

fig. 6

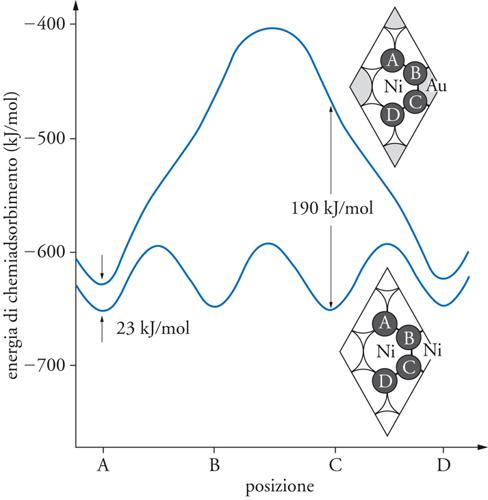
La reazione è condotta su un catalizzatore a base di nichel, che si disattiva poiché atomi di carbonio tendono a inserirsi nei cristalli di nichel. Se si opera su un monocristallo nel quale sono inseriti atomi di oro (fig. 6), si può dimostrare che la loro presenza ha un duplice effetto. Infatti, anche se diminuisce in piccola misura la velocità della reazione, riduce contemporaneamente la velocità di inserimento degli atomi di carbonio nel reticolo, limitando così il processo di disattivazione. Globalmente, pertanto, l’effetto risulta positivo.

Una prospettiva di frontiera, che sta acquistando sempre maggiore rilevanza, è la simulazione dei processi chimici che avvengono nei sistemi biologici; in particolare, risulta interessante determinare la velocità delle reazioni catalizzate da enzimi. In linea di principio, l’approccio che viene seguito non differisce da quello precedentemente descritto, se si escludono le maggiori difficoltà dovute alla complessità dei sistemi in gioco. Inoltre, molte di tali reazioni coinvolgono il moto di protoni, per cui è necessario includere l’effetto tunnel, ossia un fenomeno di natura quantistica in virtù del quale i protoni hanno una probabilità non trascurabile di attraversare le barriere di energia potenziale. Infine, è necessario tenere adeguato conto degli effetti quantistici, valutando con accuratezza l’energia di punto zero.

La complessità delle strutture molecolari che intervengono nelle reazioni biologiche ha suggerito di adottare un approccio gerarchico, originariamente introdotto per studiare la cinetica di reazioni che avvengono in soluzione. Si localizza la zona chimicamente attiva della molecola, isolandola da tutto il resto, e si tratta la dinamica dei processi che hanno luogo in tale zona mediante la meccanica quantistica e la teoria dello stato di transizione. Viceversa, i movimenti molecolari che si verificano nella parte esterna vengono descritti mediante la meccanica classica, assimilando gli atomi a sfere di van der Waals e utilizzando potenziali empirici di agevole impiego. Questo approccio viene indicato con l’acronimo QM/MM (Quantum mechanics/Molecular mechanics). Un esempio di come possa essere effettuata tale ripartizione è illustrato nella fig. 7, che si riferisce alla creatinina sciolta nel metanolo. La creatinina viene rappresentata mediante il campo elettrostatico che circoscrive la sua densità elettronica, mentre le molecole del solvente (il metanolo) sono rappresentate come sfere di van der Waals.

Lo sviluppo dei metodi di calcolo della struttura elettronica delle molecole con procedimenti ab initio sta offrendo ai chimici raffinati strumenti di calcolo, sino a qualche anno fa considerati prerogativa di ricercatori specializzati. Risulta possibile valutare, infatti, con notevole accuratezza, proprietà molecolari quali la geometria, le frequenze di vibrazione, la distribuzione delle cariche, le interazioni fra diverse molecole e la velocità delle reazioni che traggono origine dalle loro collisioni. Si deve tenere conto che la chimica computazionale è ancora una disciplina in fase di sviluppo e non ha raggiunto una piena maturità. I problemi tuttora aperti riguardano settori molto diversificati, quali lo studio delle molecole di grandi dimensioni, delle interazioni fra molecole e superfici, e dei sistemi molecolari bio-organici. Inoltre, i maggiori successi conseguiti riguardano molecole isolate o presenti in fase gassosa, mentre molto resta ancora da fare per sistemi in fase condensata. Sotto questo aspetto i metodi di calcolo delle strutture elettroniche devono opportunamente integrarsi con la termodinamica statistica.

Bibliografia

Alhambra, Cristóbal e altri, Quantum mechanical dynamical effects in an enzyme-catalyzed proton- transfer reaction, “Journal of the American Chemical Society”, 121, 1999, pp. 2253-2258.

Atkins, Peter W. - Friedman, Ronald S., Molecular quantum mechanics, 3. ed., Oxford, Oxford University Press, 1997 (trad. it.: Meccanica quantistica molecolare, Bologna, Zanichelli, 2000).

Bertani, Valeria e altri, Density functional study of the interaction of palladium clusters with hydrogen and CHx species, “Journal of physical chemistry A”, 104, 2000, pp. 11390-11397.

Besenbacher, Francis e altri, Design of a surface alloy catalyst for steam reforming, “Science”, 279, 1998, pp. 1913-1915.

Car, Roberto - Parrinello, Michele, Unified approach for density functional theory and molecular dynamics, “Physical review letters”, 55, 1985, pp. 2471- 2474.

Carpenter, Barry K., Reaction dynamics in organic chemistry, “American scientist”, 85, 1997, pp. 138-149.

Dirac, Paul, Quantum mechanics of many-electron systems, “Proceedings of the Royal Society of London”, 123, 1929, pp. 714-733.

Gao, Jali, Hybrid quantum and molecular mechanical simulations: an alternative avenue to solvent effects in organic chemistry, “Accounts of chemical research”, 29, 1996, pp. 298-305.

Head-Gordon, Martin, Quantum chemistry and molecular processes, “Journal of physical chemistry”, 100, 1996, pp. 13213-13225.

Honkala, Johanna K. e altri, Ammonia synthesis from first principles calculations, “Science”, 307, 2005, pp. 555-558.

Jensen, Frank, Introduction to computational chemistry, New York, Wiley, 1999.

Parr, Robert G. - Yang, Weikao, Densityfunctional theory of atoms and molecules, Oxford, Oxford University Press, 1989.

Pople, John A., Quantum chemical models (Nobel lecture), “Angewandte Chemie. International edition”, 38, 1999, pp. 1895-1902.

Raghavachari, Krishnan - Anderson, James B., Electron correlation effects in molecules, “Journal of physical chemistry C”, 100, 1996, pp. 12960-12973.

Truhlar, Donald G. - Garrett, Bruce C. - Klippenstein, Stephen J., Current status of transition-state theory, “Journal of physical chemistry”, 100, 1996, pp. 12771-12800.

 Wu, Tao - Werner, Hans-Joachim - Manthe, Uwe, First-principles theory for the H + CH₄ → H₂ + CH₃ reaction, “Science”, 306, 2004, pp. 2227-2229.