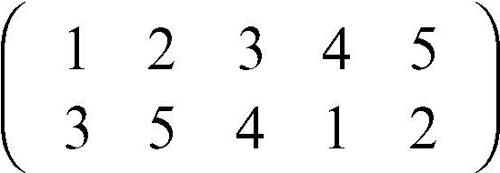ciclo

ciclo

ciclo termine che assume diversi significati a seconda del contesto.

☐ Nel calcolo combinatorio, è una particolare permutazione su n elementi, disposti in un certo ordine, che opera su k di tali elementi (con k ≤ n) mutando ognuno di essi nel successivo e l’ultimo nel primo e lasciando invariati gli altri n − k elementi. Il numero k è detto anche ordine del ciclo. Ogni permutazione si può esprimere in modo unico (a meno dell’ordine dei fattori) come prodotto di cicli disgiunti (che operano gli scambi su sottoinsiemi disgiunti). Se k = 2 si parla di trasposizione. Per esempio, la permutazione

può essere scritta come prodotto dei cicli (1, 3, 4) (2, 5), l’ultimo dei quali è una trasposizione.

☐ In topologia, il termine «ciclo» indica, in un complesso di catene C, un qualsiasi elemento del nucleo di uno dei morfismi bordo ∂_n. Il nucleo di ∂_n è il gruppo dei cicli di dimensione n di C e viene solitamente denotato con Z_n(C). Un qualsiasi suo elemento è un ciclo di dimensione n.

☐ In teoria degli algoritmi, il ciclo è uno schema di controllo consistente in un insieme ordinato di istruzioni elementari che devono essere ripetute più volte. Il numero delle ripetizioni dell’insieme di istruzioni può essere predeterminato e il ciclo ha in tal caso una caratteristica enumerativa, poiché conta, con un’apposita variabile numerica che agisce come contatore, quante volte le ripetizioni sono state eseguite, fino a raggiungere il numero prefissato. Oppure l’esecuzione delle ripetizioni è regolata dal valore di verità di una forma predicativa contenente una o più variabili di tipo qualsiasi, in base al quale viene eseguita o meno un’ulteriore ripetizione.

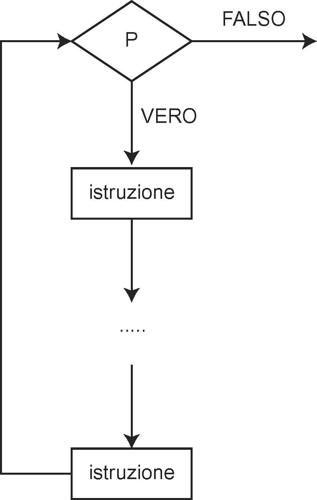
Lo schema più elementare di ciclo, in cui la sequenza di istruzione può anche non essere mai eseguita, è il seguente:

Inizialmente è posto un controllo di verità della forma P e, successivamente, la sequenza di istruzioni, da eseguire se P è vera; l’esecuzione modifica i valori delle variabili che compaiono in P e si torna a eseguire un nuovo controllo. Se P è vera, si ripetono nuovamente le istruzioni, altrimenti si esce dal ciclo. Nel caso in cui P non sia mai vera, la sequenza di istruzioni non è eseguita neppure una volta. Il ciclo è espresso da una frase del tipo:

e il numero di volte in cui si ripete la sequenza di istruzioni non è determinabile a priori: è per questa ragione che viene anche chiamato ciclo non enumerato.

Un ciclo enumerato utilizza invece una variabile contatore / che specifica il numero di ripetizioni da eseguire:

dove m e M indicano rispettivamente il valore iniziale e finale del contatore. Questa scrittura: a) assegna il valore iniziale m al contatore /; b) controlla se il valore di / è minore o uguale a M; c) incrementa di 1 il contatore a ogni passaggio (è comunque possibile formularla in modo da avere passo di incremento diverso da 1).

Un altro tipo di ciclo non enumerato si può introdurre per avere la sequenza di istruzioni eseguita almeno una volta. In questo caso la sequenza è ripetuta quando la forma predicativa è falsa, finché questa non diviene vera:

Un ciclo del tipo ripeti... finché... può essere espresso, modificando opportunamente la condizione da verificare, con un ciclo del tipo mentre... fai. Non è invece sempre possibile il contrario. Il ciclo mentre... fai... è, quindi, il caso più generale di ciclo iterativo.