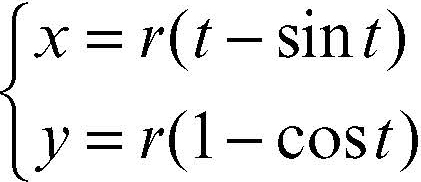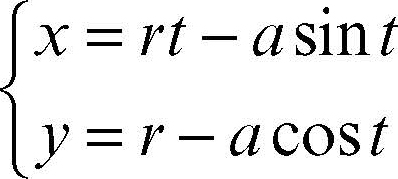cicloide

cicloide

cicloide curva piana tracciata da un punto A (detto generatore) rigidamente fissato a un cerchio che rotola, senza slittare, lungo una retta (detta base o retta direttrice). Una cicloide si dice ordinaria se il punto generatore giace sulla circonferenza del cerchio mobile; accorciata se il punto generatore è interno al cerchio; allungata se il punto è esterno al cerchio. Fissato nel piano un riferimento cartesiano Oxy e scelto come punto iniziale l’origine, la cicloide ordinaria generata dal punto appartenente a una circonferenza di raggio r che rotola sull’asse x ha equazioni parametriche

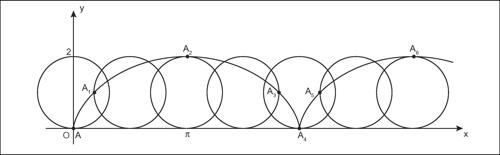
Nel grafico è rappresentata la curva che si ottiene per r = 1. La curva presenta delle cuspidi nei punti di coordinate (2πk, 0). Se il punto generatore A è a distanza a dal centro del cerchio le equazioni precedenti diventano

Le cicloidi sono curve periodiche, ossia costituite da infiniti archi uguali fra loro, corrispondenti ciascuno a un giro del cerchio mobile, e trascendenti. La cicloide ordinaria ha infinite cuspidi, l’accorciata infiniti punti di inflessione, l’allungata infiniti punti doppi. In una cicloide ordinaria, la lunghezza di ogni arco è 8r, ovvero 8 volte il raggio del cerchio generatore o 4 volte il suo diametro (teorema di Wren, dal nome dell’architetto inglese progettista della cattedrale di St. Paul a Londra), la base di ogni arco è 2πr, l’area della superficie compresa tra un arco di cicloide e la sua base è 3πr ², ovvero 3 volte l’area del cerchio generatore (teorema di Roberval).

La cicloide ordinaria ha altre interessanti proprietà: 1) è brachistòcrona, ovvero percorsa nel minimo tempo: rappresenta la traiettoria lungo la quale una massa puntiforme, soggetta al proprio peso, percorre il tragitto tra due punti nel minor tempo possibile; 2) è tautòcrona, ovvero percorsa nello stesso tempo: preso un arco completo di cicloide in un piano verticale, con la concavità verso l’alto, un punto pesante che cada lungo di esso senza attrito, a partire da uno stato di quiete e da un punto qualunque dell’arco, impiega sempre lo stesso tempo a giungere al punto più basso; in altri termini, le oscillazioni lungo un arco di cicloide sono esattamente isocrone. Proprio la scoperta della proprietà tautocrona della cicloide permise a Ch. Huygens nel 1673 di risolvere il problema della costruzione di un orologio a pendolo isocrono.

L’evoluta e l’evolvente di una cicloide sono due cicloidi identiche.

Sostituendo alla base rettilinea della cicloide una base circolare si hanno le cosiddette curve cicliche o cicloidali: epicicloide e ipocicloide, a seconda che il cerchio mobile sia tangente esternamente o internamente a quello fisso. Si chiama pericicloide la curva ottenuta in modo analogo alle precedenti quando il cerchio mobile che tocca internamente il cerchio base ha il diametro maggiore di questo.