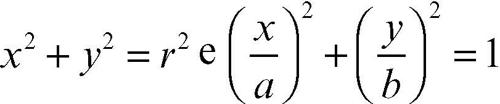cilindro

cilindro

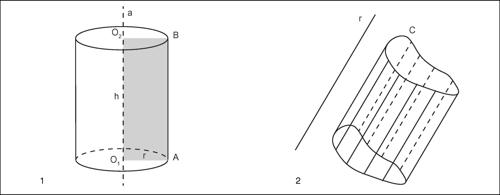
cilindro in geometria elementare e nell’uso comune, con il termine cilindro, o più propriamente cilindro finito retto (o cilindro circolare retto), si intende un solido ottenuto dalla rotazione completa di un rettangolo intorno a una retta a passante per un suo lato. La retta a è detta asse del cilindro e la distanza tra l’asse e il lato opposto del rettangolo è il raggio del cilindro. Il cilindro risulta delimitato da due superfici circolari uguali, ciascuna delle quali prende il nome di base del cilindro, e da una superficie curva, detta superficie laterale. La distanza tra le due basi è detta altezza del cilindro.

Indicati, rispettivamente, con h e r l’altezza e il raggio delle basi e con V, S_l, S_t il volume, la superficie laterale e la superficie totale del cilindro, si hanno le seguenti relazioni:

La superficie laterale del cilindro si ricava dal suo sviluppo; la superficie totale si ottiene aggiungendo alla superficie laterale la superficie delle basi; il volume del cilindro è dato dal prodotto dell’area della base per l’altezza. Se risulta h = 2r, ossia se l’altezza è uguale al diametro del cerchio di base, si ha un cilindro equilatero. In tal caso si ha che: la sua sezione con un piano passante per l’asse è un quadrato; l’area della superficie della sfera in esso inscritta è uguale a quella della sua superficie laterale (4πr ²) ed è 2/3 di quella della sua superficie totale; il volume della sfera inscritta è anch’esso pari a 2/3 di quello del cilindro. Queste relazioni fra un cilindro equilatero e la sfera in esso inscritta furono scoperte da Archimede, da cui la denominazione di cilindro di Archimede per indicare tale figura.

Più in generale, per cilindro, o più propriamente cilindro indefinito, si intende una → superficie rigata costituita da rette aventi la stessa direzione, parallele a una retta fissa (asse), e che intersecano una curva semplice C, piana o sghemba, detta curva direttrice. Se la direttrice è una conica si ha un cilindro quadrico, e a seconda che la direttrice sia un’ellisse, un’iperbole, una parabola o una circonferenza si parla di cilindro ellittico, iperbolico, parabolico o circolare. Come superficie rigata, il cilindro può essere visto quale caso particolare di cono avente come vertice un punto all’infinito; come il cono, è sviluppabile su un piano. Un cilindro indefinito circolare può essere generato dalla rotazione completa di una retta generatrice g intorno a una retta a a essa parallela, ma distinta, che costituisce l’asse del cilindro. Secando la superficie cilindrica con due piani paralleli (ma non paralleli alla generatrice), si ottiene un cilindro circolare finito; se i piani sono perpendicolari all’asse, il cilindro si dice retto; se non lo sono, le due basi sono ellissi e si ha il caso del cilindro ellittico obliquo.

In geometria analitica, l’equazione di un cilindro è del tipo ƒ(x − az, y − bz) = 0, essendo x − az = y − bz = 0 le equazioni di una retta parallela alle generatrici, e ƒ una funzione dei due argomenti x − az e y − bz. In particolare, in un riferimento cartesiano in cui l’asse z coincide con l’asse del cilindro le equazioni di un cilindro indefinito circolare e di un cilindro indefinito ellittico sono, rispettivamente: