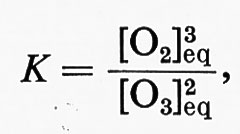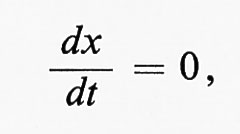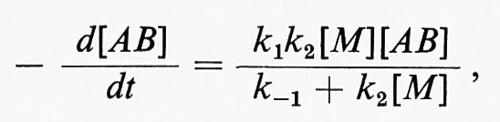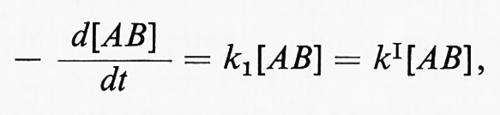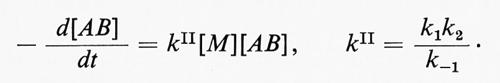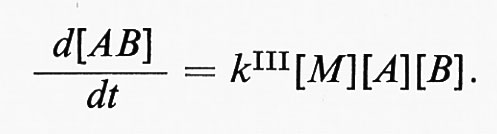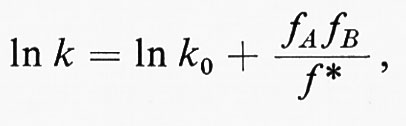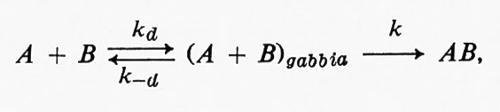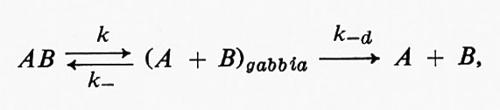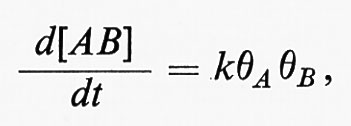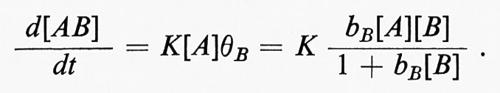Cinetica chimica

Cinetica chimica

di Nikolaj N. Semenov e Viktor N. Kondrat′'ev

Cinetica chimica

sommario: 1. Cenni storici. 2. Concetti generali della cinetica chimica. 3. Cinetica delle reazioni in fase gassosa: a) reazioni monomolecolari; b) reazioni bimolecolari; c) reazioni trimolecolari; d) reazioni a catena. 4. Reazioni in fase liquida: a) guscio di solvatazione, attività; b) effetto gabbia; c) catalisi acida; d) reazioni a catena in fase liquida. 5. Catalisi eterogenea. 6. Reazioni in fase solida. □ Bibliografia.

1. Cenni storici

La cinetica chimica tratta delle velocità e dei meccanismi delle reazioni chimiche. Il suo scopo fondamentale è quello di fornire una corretta nozione del meccanismo di una reazione chimica che si svolge in certe condizioni, e di utilizzarla per il calcolo più accurato possibile della velocità di reazione. Queste sono le richieste poste alla cinetica chimica dall'industria chimica e dalla tecnologia dei processi chimici.

Nello sviluppo generale della cinetica chimica si possono distinguere tre principali indirizzi. Il primo è connesso con le reazioni semplici e reversibili e con l'equilibrio chimico. Questo indirizzo, particolarmente avvalorato da J. H. van't Hoff (1852-1911), conduce all'idea di stadio di una reazione chimica, intesa come interazione tra un certo numero di molecole, e alla precisa formulazione del concetto di equilibrio chimico. Il secondo indirizzo, riguardante le reazioni complesse, ha messo in luce quanto sia complicata la maggior parte delle reazioni chimiche e ha portato al concetto di meccanismo di reazione, inteso come una rete di reazioni elementari. Il terzo indirizzo, concernente le reazioni chimiche a catena, è rimasto per lungo tempo separato dal principale cammino dello sviluppo della chimica, dal momento che l'importanza delle reazioni a catena fu compresa e apprezzata per la prima volta soltanto all'inizio del XX secolo.

Il primo indirizzo ebbe origine dai molti tentativi effettuati per caratterizzare quantitativamente il concetto di ‛affinità chimica', cioè la capacità di una specie di reagire con altre specie.

Un passo essenziale nello sviluppo dell'aspetto quantitativo nella storia delle trasformazioni chimiche fu compiuto da Cl.-L. Berthollet (1801). Questi, infatti, mentre studiava la produzione del salnitro e la formazione del sale nei laghi, giunse alla conclusione che lo sviluppo delle reazioni chimiche si correlava alla massa delle sostanze reagenti, alle loro proprietà fisiche e chimiche e anche alle condizioni in cui la reazione procedeva. Egli pensò che queste ultime potessero influenzare l'affinità e far così perdere ad essa il significato di caratteristica cinetica generale. Nel 1803 Berthollet propose un nuovo concetto di processo chimico, implicante due reazioni che procedono simultaneamente in direzioni opposte. Questa fu l'origine della teoria dell'equilibrio chimico, che si sviluppò nella seconda metà del XIX secolo.

Una definizione matematica concisa delle condizioni dell'equilibrio chimico fu data da C. M. Guldberg e P. Waage (1864-1867) per la reazione A + B ⇄ A′ + B′:

kC_A C_B = k′C_A′C_B′,

detta ‛legge dell'azione di massa', dove C_A, C_B, C_A′ e C_B′ sono le concentrazioni all'equilibrio, k e k′ sono delle costanti che furono denominate da van't Hoff ‛costanti di velocità'.

Le leggi più generali per semplici reazioni chimiche furono trattate da van't Hoff, il quale introdusse le definizioni di reazioni mono-, bi-, tri- e plurimolecolari, a seconda delle molecole coinvolte in esse. Poiché van't Hoff considerava come generali i primi tre tipi di reazione, egli tentò di stabilire, sebbene in modo del tutto formale, la dipendenza delle costanti di velocità dalla temperatura.

Facendo uso dell'espressione termodinamica per la costante di equilibrio:

K = exp(S/R − Q/RT),

dove S è l'entropia e Q il calore di reazione, e assumendo che

K = k/k′,

van't Hoff espresse le costanti di velocità della reazione diretta (k) e della reazione opposta (k′) secondo la legge seguente:

k = a exp(−E/RT) e k′ = b exp[(−E + Q)/RT].

Nel 1889 fu pubblicata la famosa memoria di 5. A. Arrhenius che introduceva il concetto di ‛energia di attivazione' intesa come la grandezza più importante della cinetica chimica. Arrhenius formulò l'ipotesi che soltanto le molecole che posseggono un determinato eccesso di energia E, le cosiddette, ‛molecole attive', possano partecipare alla reazione. La seguente espressione per la costante di velocità:

k = a exp(−E/RT)

ha preso il nome di ‛legge di Arrhenius'.

Negli anni trenta M. Polanyi e H. Eyring svilupparono la teoria secondo cui si forma un complesso attivato come stato di transizione per ogni stadio elementare di una reazione. Essi avanzarono l'ipotesi che la formazione e la successiva conversione di questo complesso nei prodotti di reazione potesse verificarsi solo quando l'energia del complesso fosse stata più alta dell'energia di attivazione. La teoria del complesso attivato ha mantenuto il suo significato fino a oggi. Qualche anno dopo, un importante contributo alla teoria delle reazioni elementari fu apportato dalla meccanica quantistica.

Di grande valore per la cinetica delle reazioni chimiche è l'equazione di J. N. Brönsted (1924), che mette in relazione la costante di velocità della reazione con quella di dissociazione di un acido o di una base deboli che agiscono da catalizzatori.

I primi risultati quantitativi sulla relazione tra reattività e struttura furono ottenuti da J. H. van't Hoff e W. Ostwald (1884). Il primo tentativo di inquadrare in modo sistematico i risultati sperimentali riguardanti le proprietà chimiche di vari composti, intese come funzioni delle loro strutture, deve essere attribuito allo stesso van't Hoff (1900).

La cinetica delle reazioni chimiche complesse cominciò a svilupparsi nella metà del sec. XIX principalmente come risultato di ricerche sulle reazioni chimiche in soluzione. Furono così scoperte le reazioni ‛accoppiate' ‛coniugate' Ostwald (1900) propose per esse un meccanismo che ha pure fornito una spiegazione al fenomeno dell'accelerazione iniziale, che si osserva in molte reazioni.

Nello stesso periodo cominciò lo sviluppo della cinetica dell'ossidazione. Le reazioni a catena furono scoperte da E. A. M. Bodenstein nel 1913. Questi osservò che il rendimento quantico, cioè il numero di molecole che reagiscono per ogni quanto di luce assorbito, raggiungeva valori molto elevati per certe reazioni fotochimiche. Tuttavia, il fenomeno dei limiti di esplosione caratteristico delle reazioni a catena - vale a dire la possibilità che si abbia l'esplosione di una miscela di gas soltanto entro certi intervalli di valori di pressione e di temperatura - era stato osservato già da tempo. Per esempio, A. von Humboldt e J.-L. GayLussac (1805), H. Davy (1817) e altri avevano osservato il fenomeno dei limiti di esplosione dell'idrogeno sin dagli inizi del sec. XIX.

Questo fenomeno è stato interpretato da N. N. Semenov e C. N. Hinshelwood e dai loro allievi mediante la teoria delle ramificazioni a catena avanzata da Semenov (1926-1934).

2. Concetti generali della cinetica chimica

Dal punto di vista del meccanismo di reazione, le reazioni chimiche possono essere classificate come semplici e complesse. Le prime avvengono in un solo stadio e si distinguono in reazioni del primo, secondo e terzo ordine, o come reazioni mono-, bi- e trimolecolari, in relazione al numero di molecole (uno, due, tre) che esse interessano. La decomposizione di qualsiasi molecola che possegga una energia sufficiente è una reazione semplice, del primo ordine o monomolecolare. Più numerose sono le reazioni del secondo ordine, che interessano due molecole reagenti fra di loro. La reazione NO + Cl₂ + NO = 2NOCl può essere data come esempio di reazione del terzo ordine o trimolecolare.

La velocità di una reazione chimica semplice è proporzionale al numero degli urti tra le molecole reagenti nell'unità di tempo. Secondo la teoria cinetica, esso è proporzionale al prodotto delle concentrazioni.

Le velocità di reazione per le reazioni monomolecolari (conversione della specie A), bimolecolari (interazione tra A e B) e trimolecolari (interazione tra A, B e C) sono fornite dalle espressioni

w₁ = k₁[A], w₂ = k₂[A][B], w₃ = k₃[[A][B][C],

dove k₁, k₂ e k₃ sono le costanti (o coefficienti) di velocità per tali reazioni, che dipendono dalla temperatura; [A], [B] e [C] sono le concentrazioni delle specie A, B e C. Il numero dei fattori che entrano nell'equazione della velocità di reazione e che esprimono le concentrazioni determina l'ordine di reazione ν = 1, 2, 3 per reazioni rispettivamente del primo, del secondo e del terzo ordine.

L'ordine di una reazione, determinato sperimentalmente, non sempre coincide con la ‛molecolarità' della reazione stessa, quale risulterebbe dai numero delle molecole partecipanti.

La dipendenza dalla temperatura della velocità di reazione, di qualsiasi ordine, è espressa da:

k = a(T) exp(−E/RT).

Di solito il fattore pre-esponenziale a, così come il valore E, chiamato ‛energia di attivazione', sono dipendenti dalla temperatura solo in piccola misura, entro un certo intervallo di temperature, e possono quindi essere considerati costanti per una data reazione. In questo caso l'espressione della costante di velocità si riduce a

k = a exp(−E/RT)

e si chiama espressione di Arrhenius. L'energia di attivazione è determinata dalla barriera di energia potenziale che deve essere superata, a spese dell'energia delle sostanze reagenti, per far avvenire la reazione.

Le costanti di velocità, il fattore a e l'energia di attivazione E sono funzioni della reattività delle specie interessate. La reattività dipende dalla struttura delle sostanze reagenti ed è decisiva per la cinetica, per la velocità e per il decorso di una reazione. Essa è una funzione della mobilità degli atomi o dei gruppi di atomi in una molecola, che dipende a sua volta dalla distribuzione delle cariche e dei legami chimici intramolecolari, dalla forza dei legami e da altre caratteristiche fisiche della struttura molecolare. Per esempio, gli atomi di idrogeno appartenenti ai gruppi CH₂ degli alcani sono più mobili di quelli appartenenti ai gruppi CH₈. Le interazioni fra le specie reagenti e le molecole del mezzo ambiente (del solvente o della matrice solida) hanno un effetto essenziale sulla reattività.

Di grande importanza per la cinetica chimica è la notevole differenza tra la reattività degli atomi e dei radicali con valenze libere e la reattività delle molecole sature. Mentre l'energia di attivazione per la maggior parte delle reazioni molecolari raggiunge di solito qualche decina di kcal/mole, quella per le reazioni di atomi e radicali con molecole o radicali arriva ad alcune kcal/mole, raggiungendo o superando raramente le 10 kcal/mole. Per questa ragione a una temperatura di 1.000 °K, ad esempio, allorché la reazione molecolare diviene misurabile, la velocità di una reazione che coinvolge radicali sarà spesso parecchi milioni di volte più alta.

L'elevata reattività degli atomi e dei radicali spiega il verificarsi relativamente raro di reazioni semplici tra molecole sature. Sebbene la produzione di atomi e di radicali nelle reazioni termiche sia difficoltosa, tuttavia le reazioni che interessano atomi e radicali sono predominanti.

Reattività molto alte si riscontrano anche nel caso di atomi e molecole ionizzati che partecipano a reazioni esotermiche in fase gassosa con molecole neutre senza energia di attivazione, cioè senza una barriera di energia potenziale.

Le reazioni complesse implicano il verificarsi di parecchi stadi. La formazione di composti intermedi più attivi di quelli iniziali, per esempio perossidi o aldeidi nel processo di ossidazione degli idrocarburi, è caratteristica delle reazioni complesse.

Gli atomi, i radicali o gli ioni che appaiono in un gran numero di reazioni sono gli intermedi più attivi.

Un esempio di una tra le più semplici reazioni complesse è la decomposizione termica dell'ozono, che implica due stadi successivi:

0₂ ⇄ , 0₂, + 0

0 + 0₃ ⇄ 0₂ + 0₂ .

L'ossigeno atomico è la specie attiva in questa reazione. Quest'esempio mostra chiaramente la differenza tra le vere equazioni della reazione e l'equazione, così detta ‛stechiometrica', che esprime il bilancio totale di una reazione. Nell'esempio considerato l'equazione stechiometrica sarà:

20₂ = 30₂.

Le concentrazioni all'equilibrio del composto iniziale [O₃]_eq e del prodotto della reazione [O₂]_eq sono legate dalla seguente relazione:

in cui K è la costante di equilibrio.

Come detto sopra, gli atomi e i radicali hanno, rispetto alle molecole sature, un'elevata reattività. Di conseguenza, la velocità con cui si decompongono è spesso molto prossima a quella con cui si formano; la concentrazione del prodotto intermedio può quindi considerarsi stazionaria e può essere definita da

in cui x è la concentrazione del prodotto intermedio e t è il tempo. La possibilità di usare condizioni stazionarie (steady state), particolarmente per le reazioni complesse che implicano parecchi prodotti intermedi, permette di sostituire le equazioni cinetiche di tipo differenziale con equazioni algebriche, il che rende molto più agevole il calcolo delle velocità delle reazioni complesse. Questo metodo, usato per la prima volta da Bodenstein nella cinetica chimica e sviluppato in seguito da Semenov, è detto metodo delle concentrazioni stazionarie di Bodenstein-Semenov.

Ogni reazione chimica semplice, così come qualsiasi stadio elementare di una reazione complessa, può procedere in senso diretto o in senso inverso, cioè tali reazioni sono di tipo ‛reversibile'. Considerando la reazione

NO + Cl₂ + NO = 2NOCl

come diretta, la reazione inversa sarà

2NOCl = 2NO + Cl₂.

Indicando con k e k_- rispettivamente le costanti di velocità della reazione diretta e di quella inversa, si ottiene all'equilibrio termodinamico

k[NO]²_eq[Cl₂]_eq = k_- [N0Cl]²_eq

dove (NO]_eq, [Cl₂]_eq e [NOCI]²_eq, sono le concentrazioni all'equilibrio, legate fra loro per mezzo della costante di equilibrio

K = [NOCl]²_eq/[NO]²_ep[Cl₂]_eq.

La costante di equilibrio può così essere espressa da:

K = k/k_-.

Per molte reazioni K si può calcolare in base alla teoria statistica: in tal modo l'espressione precedente può essere usata per calcolare K_- se è nota k, o viceversa. Ciò è impossibile nel caso delle reazioni complesse, per le quali la costante di equilibrio, espressa sempre come rapporto tra il prodotto delle concentrazioni all'equilibrio delle specie finali e il prodotto di quelle iniziali, non può essere il rapporto delle costanti principali di velocità, cosa che in questo caso non avrebbe senso.

Nell'esempio precedente della decomposizione dell'ozono, il secondo stadio della reazione segue il primo. Tali reazioni sono dette ‛consecutive'. La velocità di una reazione consecutiva è funzione del suo stadio più lento, che risulta quindi quello che controlla la velocità.

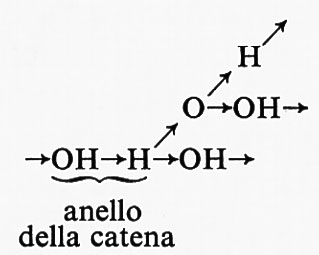
Esiste anche una classe di ‛reazioni parallele'. Le cosiddette ‛reazioni accoppiate' (‛coniugate') appartengono a questa classe. La loro particolarità consiste nel fatto che una delle reazioni parallele (primaria) è indipendente dall'altra, ma quest'ultima (secondaria) può verificarsi solo insieme alla prima. Lo sviluppo della reazione secondaria è dovuto alla presenza di un prodotto intermedio attivo formatosi nella reazione primaria, il quale funziona da anello di congiunzione tra le due reazioni.

A titolo di esempio, citiamo l'ossidazione simultanea dell'idrogeno e del monossido di carbonio. L'ossidazione del monossido di carbonio, contrariamente a quella dell'idrogeno, avviene, in assenza di impurezze, solo ad altissime temperature; tuttavia, essa si svolge molto più rapidamente in presenza di idrogeno. Nell'esempio citato l'intermedio idrossile (OH), formatosi dall'ossidazione dell'idrogeno, reagendo col monossido di carbonio, viene a costituire l'anello di congiunzione tra le due reazioni.

Le reazioni ‛catalitiche', cioè quelle che hanno luogo in presenza di un composto estraneo (catalizzatore) che nel corso della reazione o non si consuma affatto oppure si consuma in quantità trascurabile, assomigliano, nel loro meccanismo, alle reazioni accoppiate. Per le reazioni in fase gassosa o liquida, il catalizzatore è rappresentato da molecole o da ioni e si parla allora di ‛catalisi omogenea'. Anche un corpo solido può fungere da catalizzatore; in tal caso la reazione avverrà completamente o parzialmente sulla sua superficie e si parla allora di ‛catalisi eterogenea'. Proprio come accade nelle reazioni accoppiate, l'interazione tra una delle sostanze reagenti e il catalizzatore produce un complesso intermedio attivo, che entra in una reazione secondaria con un composto iniziale relativamente inerte e lo guida verso la reazione principale. Un esempio di catalisi omogenea è l'azione di accelerazione del bromuro di idrogeno sull'ossidazione del propano in fase gassosa o quella degli ioni dei metalli di transizione nelle reazioni che avvengono in fase liquida (v. catalisi: catalisi omogenea; catalisi eterogenea).

La catalisi omogenea, che consente la realizzazione di processi chimici complessi a temperature prossime alla temperatura ambiente, è di grande importanza pratica.

I prodotti intermedi o quelli finali spesso accelerano, cioè catalizzano, la reazione. Tali reazioni si chiamano autocatalitiche. Il fenomeno dell'autocatalisi è dovuto sia alla formazione più rapida di specie attive, radicali o ioni, come risultato di successive trasformazioni di prodotti intermedi o finali, sia alla formazione diretta di prodotti intermedi attivi.

Molto spesso le reazioni sono avviate da piccole quantità di sostanze dette ‛iniziatori', che formano rapidamente dei radicali o dei complessi attivi e si consumano nel corso della reazione. Vi sono altre sostanze, dette ‛inibitori', che rallentano invece la reazione.

3. Cinetica delle reazioni in fase gassosa

I meccanismi di alcune reazioni sono simili sia in fase gassosa sia in soluzione; tuttavia, quelli riguardanti la fase gassosa sono stati studiati più in dettaglio e perciò sono quelli citati di preferenza.

Una reazione chimica complessa è il risultato di più stadi elementari consecutivi o paralleli. Ogni stadio può essere una reazione del primo, del secondo o del terzo ordine. Saranno descritte qui di seguito le caratteristiche peculiari delle reazioni monomolecolari, bimolecolari e trimolecolari.

a) Reazioni monomolecolari

Le reazioni monomolecolari consistono nella decomposizione o nella isomerizzazione di una molecola. Il meccanismo di una reazione monomolecolare (secondo F. A. Lindemann) implica: lo stadio di ‛attivazione', in cui l'energia necessaria per la reazione è fornita alla molecola dagli urti con le altre molecole; lo stadio di ‛disattivazione', che ha come risultato la perdita di questa energia e, infine, un terzo stadio, che coincide con la reazione monomolecolare propriamente detta. Gli stadi di attivazione (1) e di disattivazione (-1) sono del secondo ordine, mentre la trasformazione monomolecolare (2) è del primo ordine. Indicando con k₁, k_-1 e k₂ le tre costanti per gli stadi principali della reazione di una molecola AB e assumendo una condizione stazionaria della concentrazione delle molecole attive, si ottiene per la costante di velocità la seguente espressione

dove [M] sta a indicare ogni specie partecipante allo stadio di attivazione o a quello di disattivazione. Ne segue che alle alte pressioni, quando k₂[M] > > k_-1, la velocità di reazione sarà espressa dalla

cioè la reazione sarà del primo ordine. Alle basse pressioni, invece, la reazione sarà del secondo ordine

Da quanto detto sopra si comprende la grande importanza per la cinetica chimica dello scambio di energia indotto dagli urti, che rende conto dell'attivazione e della disattivazione. Generalmente, l'energia vibrazionale è quella determinante per l'attivazione. A un'elevata velocità di scambio dell'energia vibrazionale (rilassamento vibrazionale veloce), si può considerare che la reazione abbia luogo in condizioni di equilibrio termodinamico.

b) Reazioni bimolecolari

Le reazioni bimolecolari sono generalmente del secondo ordine. Il meccanismo di queste reazioni, esattamente come quello delle reazioni monomolecolari, mostra due stadi consecutivi: quello dell'attivazione e quello della reazione propriamente detta. Quando il secondo stadio è più lento, la velocità w della reazione

X + Y = prodotti

sarà espressa da

w = k[X][Y],

dove k è la costante di velocità, [X] e [Y] sono le concentrazioni dei reagenti. Questa espressione è valida per la maggior parte delle reazioni di radicali con molecole. Quando lo stadio di attivazione è più lento, per esempio nella reazione H₂ + D₂ = 2HD, l'espressione della velocità è più complicata:

w = k[X]^x[Y]^y[M]^m,

dove x, y ed m sono numeri frazionari (x + y + m = 2), e [M] è la concentrazione del composto esterno che partecipa, con X e Y, all'attivazione delle molecole reagenti. In questo caso, esattamente come nelle reazioni monomolecolari, vi è una perturbazione della distribuzione di equilibrio dell'energia.

L'indagine delle reazioni bimolecolari in pennelli molecolari dimostra che alcune reazioni impiegano un tempo paragonabile a quello caratteristico dell'urto, cioè dell'ordine di 10^-13 s, mentre altre hanno luogo attraverso un complesso intermedio di vita più o meno lunga, A + B → AB* → C + D. Questa differenza può essere messa in evidenza dalla distribuzione angolare dei prodotti di reazione C e D, nonché dalla forma e dalla distribuzione dell'energia dei prodotti stessi.

Le reazioni bimolecolari possono anche essere di ricombinazione, A + B → AR, compresa la ricombinazione di atomi e radicali; per basse pressioni tali reazioni di ricombinazione risultano del terzo ordine:

c) Reazioni trimolecolari

A differenza delle reazioni monomolecolari e bimolecolari, le reazioni trimolecolari, che consistono in una reazione semplice che interessa tre specie, sono sempre del terzo ordine:

La perturbazione della distribuzione di equilibrio dell'energia dipende da due fattori. Il primo consiste nella diminuzione della concentrazione delle molecole ricche di energia che avviene nelle reazioni endotermiche, per esempio nella dissociazione molecolare. Il secondo consiste nella liberazione di energia, particolarmente importante per le reazioni esotermiche. Quando la reazione è così veloce, specialmente alle alte temperature, che il tempo di reazione è più breve di quello del rilassamento termico, la distribuzione dell'energia differirà più o meno dalla distribuzione di equilibrio di Maxwell-Boltzmann. La perturbazione dell'equilibrio energetico avrà naturalmente un effetto sulla reattività delle molecole che prendono parte alla reazione. In tal modo, le velocità di reazione in un sistema in equilibrio e in uno caratterizzato da equilibrio perturbato saranno differenti.

Tuttavia, la perturbazione dell'equilibrio energetico, come si deduce da indagini di cinetica, è in genere trascurabile, nell'ambito delle basse e delle medie temperature, a causa dei processi di rilassamento relativamente rapidi.

d) Reazioni a catena

Le reazioni a catena, quelle cioè in cui un centro attivo induce la trasformazione di molte molecole del componente iniziale, rappresentano un'importante classe di reazioni chimiche complesse di grande valore pratico. Una reazione di tale tipo è possibile quando la specie attiva che partecipa alla reazione è sostituita da un'altra capace di far propagare la reazione. Questo è il caso, per esempio, della reazione a catena tra il cloro e l'idrogeno, in cui gli atomi di cloro e di idrogeno costituiscono i centri attivi. Il meccanismo di questa reazione comprende i seguenti stadi elementari:

La formazione iniziale di atomi di cloro (0), per dissociazione termica delle molecole di cloro o per qualche azione esterna, per esempio della luce, è seguita dagli stadi (1) e (2), chiamati stadi di propagazione della catena. Questi, dando luogo alla rigenerazione del centro attivo iniziale, cioè dell'atomo di cloro, costituiscono un anello della catena.

Più numerose sono le molecole di H₂ e Cl₂ che partecipano alla reazione, più lunga sarà la catena. Il rendimento quantico della reazione fotochimica tra il cloro e l'idrogeno, studiata da Bodenstein, che scopri le reazioni a catena, arriva a 100.000. Ciò significa che si formano in media 100.000 molecole del prodotto di reazione, HCl, per ogni atomo primario di cloro generato dalla luce, cioè la lunghezza della catena è di circa 100.000. La catena termina con la distruzione di uno dei centri attivi per adsorbimento sulla parete del reattore o per assorbimento da parte di una molecola estranea o per altre cause.

Le reazioni a catena si distinguono in reazioni a catena ‛semplice' (non ramificata), per esempio quella del cloro con l'idrogeno sopra menzionata, e a catena ‛ramificata'. Le reazioni a catena ramificata sono caratterizzate dal fatto che un centro attivo, che partecipa alla reazione, è sostituito da altri due o tre. Un centro appena formato può iniziare un nuovo ramo della catena, cioè la catena diventa ramificata.

Segue da quanto detto sopra che il meccanismo di una reazione a catena implica degli stadi elementari di inizio, di propagazione, di ramificazione e di interruzione della catena. Questi stadi possono costituire reazioni del primo, del secondo e del terzo ordine.

Un esempio classico di una reazione a catena ramificata è quella tra l'idrogeno e l'ossigeno, in cui i centri attivi sono gli atomi H e O e i radicali OH. La ramificazione della catena s'inizia con l'interazione tra gli atomi di il e le molecole di ossigeno, H + O₂ = OH + O, seguita dalla reazione O + H₂ = OH + H. Come risultato di queste reazioni il centro attivo, l'atomo di H, è sostituito da un altro atomo di H e da due radicali OH, che danno luogo a tre nuovi rami della catena.

La formazione di concentrazioni di specie attive (in questo caso H, O e OH) eccedenti di molti ordini di grandezza i valori normali di equilibrio è caratteristica di questa e di tutte le altre reazioni a catena ramificata. Nella reazione dell'idrogeno con l'ossigeno, la ramificazione avviene a ogni anello della catena

Una catena di questo tipo è detta ‛completamente ramificata'. Reazioni a catena in cui non ci sono ramificazioni a ogni anello della catena sono considerevolmente più frequenti.

La frequenza delle ramificazioni determina la velocità della reazione a catena, ma non ha alcun effetto sulle sue leggi cinetiche, come la legge di accelerazione e i limiti di esplosione.

Per una frequenza sufficientemente alta di ramificazioni si ha una rapida accelerazione della reazione; variazioni molto piccole dei parametri di reazione, come la temperatura, la pressione, la composizione della miscela e il diametro del reattore, possono provocare la transizione da una reazione lenta, avente una velocità quasi nulla, a una reazione molto veloce, di natura esplosiva.

L'esplosione generalmente avviene solo qualche tempo dopo l'inizio della reazione, quando la velocità di questa raggiunge un certo valore critico. Questo intervallo di tempo, chiamato ‛periodo di induzione', dura da qualche frazione di secondo ad alcune ore. Se non viene raggiunto il valore critico, per esempio a causa del consumo dei composti iniziali, non vi sarà esplosione.

La ramificazione cosiddetta ‛degenere', che ha una grande importanza per la cinetica delle reazioni nelle fasi gassosa e liquida, è trattata nella teoria di Semenov delle reazioni a catena. Il concetto di ramificazione degenere è stato formulato studiando la cinetica di molte reazioni lente, caratterizzate da certi specifici aspetti della catena. Si è trovato, in particolare, che queste reazioni seguono l'usuale legge esponenziale, risultando però molto lente. La teoria della ramificazione degenere implica che la reazione proceda secondo il meccanismo di una semplice reazione a catena, ma che di tanto in tanto vi appaia un composto intermedio stabile che entri in una reazione collaterale e formi nuovi centri attivi capaci di produrre un nuovo ramo della catena. In certi casi si pensa che il composto intermedio si decomponga in radicali.

La teoria delle reazioni a catena ramificata è stata sviluppata da Semenov. Egli ha dimostrato, in particolare, che la velocità di una reazione che si conclude nell'esplosione o nell'accensione della miscela dipende dal tempo secondo la legge exp(ϕt), dove ϕ è la differenza tra la velocità di formazione dei centri attivi in eccesso (velocità di ramificazione della catena) e quella di distruzione dei centri attivi (velocità di terminazione della catena). Ne segue che un'esplosione può avvenire solo quando la velocità di ramificazione è più alta di quella di terminazione, cioè per ϕ > 0. Se ϕ = 0 si ha la condizione per la transizione da una reazione lenta a una esplosiva. Poiché la ramificazione è una reazione del secondo ordine e la distruzione dei centri attivi è del primo ordine, quando i centri sono adsorbiti dalla parete del reattore (terminazione eterogenea della catena), o del terzo ordine, per una terminazione omogenea della catena connessa con la formazione di un radicale stabile inattivo (come, per es., nella reazione H + O₂ + M = HO₂ + M, M essendo una qualsiasi specie), la condizione ϕ = O sarà espressa da un'equazione quadratica nella pressione. Le due soluzioni di questa equazione p₁(T) e p₂(T), che sono funzioni della temperatura e della composizione della miscela, rappresentano i limiti della regione di esplosione. Entro l'intervallo di temperatura dell'esplosione e per p 〈 p₁ o p > p₂ la reazione è lenta, mentre per p₁ 〈 p 〈 p₂ sarà di natura esplosiva. I valori p₁ e p₂ si chiamano limiti di accensione ‛inferiore' e ‛superiore' (o, rispettivamente, primo e secondo).

L'esplosione termica è di un genere essenzialmente differente. Essa generalmente avviene quando la velocità di reazione diventa così alta (principalmente ad alte pressioni) che la velocità con cui si genera calore non è più compensata dalle perdite caloriche. La temperatura del gas aumenterà continuamente e a un certo valore avverrà l'esplosione. In questo caso, il riscaldamento della miscela sarà la causa diretta dell'esplosione, mentre in un'esplosione a catena il calore liberato non sarà la causa, bensì la conseguenza. Da quanto detto sopra segue che l'esplosione termica è possibile sia per una catena ramificata sia per una catena non ramificata.

Come si è detto prima, la ramificazione avviene per la reazione di un atomo o di un radicale con una molecola del composto iniziale, da cui hanno luogo due o tre nuovi radicali attivi. È stato detto che la ramificazione degenere di una catena è possibile anche come risultato della decomposizione di un composto intermedio in radicali. Tuttavia, non si può escludere il possibile contributo alla ramificazione dato dalle specie ricche di energia che compaiono negli stadi di una catena esotermica.

E. A. M. Bodenstein, J. A. Christiansen e H. A. Kramers furono i primi a porre l'attenzione sul fattore energia. Essi avanzarono l'ipotesi che le molecole eccitate (ricche di energia) costituissero i portatori attivi della catena (concetto della ‛catena energetica'). Tuttavia, ulteriori indagini sembrarono dimostrare che le catene energetiche non esistono. In seguito, Semenov ha mostrato il possibile contributo di molecole ricche di energia al processo di ramificazione. Si conoscono oggi certe reazioni a catena la cui ramificazione è dovuta al fattore energia (ramificazione energetica). Un esempio convincente di quanto detto è quello della reazione tra il fluoro e l'idrogeno. L'alta esotermicità della fase di propagazione della catena

H + F₂ = HF + F

determina l'apparire di molecole HF aventi un'energia vibrazionale sufficiente per la dissociazione del fluoro in atomi (circa 36 kcal/mole). Così, a differenza della reazione a catena tra il cloro e l'idrogeno, che è semplice, non ramificata, quella tra il fluoro e l'idrogeno è una tipica reazione a catena ramificata: cosa che può dedursi, in particolare, dall'esistenza del primo e del secondo limite di esplosione.

4. Reazioni in fase liquida

Le reazioni in fase liquida differiscono da quelle in fase gassosa per la bassa velocità di diffusione dei reagenti (il coefficiente di diffusione per i gas è di circa 1 cm²/s e quello per i liquidi è di circa 10^-6 cm²/s) e per l'effetto del mezzo sulla reattività dei reagenti.

Due stadi consecutivi, quello di diffusione e quello cinetico, sono caratteristici delle reazioni in fase liquida. Poiché la velocità di reazione è determinata dallo stadio più lento, alle alte velocità di diffusione la reazione sarà indipendente dai fattori che influenzano la diffusione, in particolare dalla viscosità del mezzo, mentre, se i reagenti sono dei radicali, nelle cosiddette ‛reazioni omolitiche', o ioni, nelle ‛reazioni eterolitiche', lo stadio cinetico è generalmente più veloce e la velocità complessiva di reazione sarà soprattutto funzione della diffusione.

a) Guscio di solvatazione, attività

Il comportamento dei reagenti in una fase liquida dipende in gran parte dalla loro interazione col mezzo; a tale fenomeno si dà il nome di ‛solvatazione'. La solvatazione modifica l'energia libera dei reagenti, la distribuzione della loro densità elettronica, le loro distanze interatomiche, ecc. L'effetto delle molecole del solvente sulle proprietà dei reagenti in una soluzione aumenta con la forza del legame ed è particolarmente pronunciato per le specie cariche (ionizzate). Quando l'interazione tra la specie in soluzione e le molecole del guscio di solvatazione dà luogo alla formazione di complessi del tipo donatore-accettore o di legami a idrogeno, allora essa è detta ‛solvatazione specifica'. Una specie solvatata specificamente costituisce, infatti, un nuovo composto intermedio, spesso in equilibrio con la specie iniziale non solvatata.

L'effetto della solvatazione sulla velocità di reazione è generalmente trattato in base alla teoria del complesso attivato. Secondo questa teoria, il logaritmo della costante della velocità di reazione per un dato solvente è dato dalla relazione

dove k₀ è la costante di velocità per la stessa reazione in un solvente di riferimento o nella fase gassosa, f_A, f_B e f* sono i'coefficienti di attività' per le specie iniziali A e Re per il complesso attivato. I coefficienti di attività danno una misura della variazione nell'energia libera dei rea genti causata dalla solvatazione. In teoria, se k₀ è nota, la costante di velocità k può essere calcolata per qualunque solvente.

b) Effetto gabbia

Affinché sia possibile una reazione chimica tra i reagenti A e B, questi devono avvicinarsi l'uno all'altro a una certa distanza r. A questa distanza, entrambe le specie avranno un guscio di solvatazione comune e si troveranno, per così dire, nella stessa gabbia. Più alta è la viscosità del mezzo, più difficili saranno la penetrazione dei reagenti nella gabbia e la fuoriuscita da essa. Quando sono nella gabbia, i reagenti subiscono da 10 a 100 collisioni per ml al secondo. All'azione di schermo della gabbia si dà il nome di ‛effetto gabbia'.

Il meccanismo della reazione A + B = AB è

dove k_d e k_-d sono le costanti di velocità per la diffusione dei reagenti all'interno e fuori dalla gabbia, rispettivamente, e k è la costante di velocità dello stadio chimico della reazione. Il meccanismo della reazione AB = A + B è

dove k e k_- sono le costanti di velocità delle reazioni diretta e inversa che interessano le molecole AR.

L'effetto gabbia sarà di maggiore o minore importanza a seconda della relazione tra le costanti di velocità k_d, k_d, k_-d, e k_-.

Come fu osservato per la prima volta da J. Franck e E. Rabinowitsch nel 1934, l'effetto gabbia è più pronunciato per il ‛condo caso, quando k_-d è considerevolmente maggiore di k_-, cioè quando la diffusione di A e B fuori dalla gabbia costituisce lo stadio che controlla la velocità di reazione.

c) Catalisi acida

La catalisi acida in soluzioni acquose di acidi minerali forti (H₂SO₄, HCl, H₃PO₄, ecc.) rappresenta un tipo comune di reazione eterolitica in fase liquida.

Un reagente iniziale B di bassa attività, rappresentante una base debole, si converte prontamente, in ambiente acido, in una forma attiva BH+ che partecipa alle ulteriori fasi della reazione.

d) Reazioni a catena in fase liquida

Le reazioni a catena in fase liquida interessano ioni e specie neutre radicaliche che ne costituiscono i centri attivi. L'ossidazione organica, che avviene per mezzo del meccanismo della ramificazione degenere, costituisce una vasta classe di reazioni a catena in fase liquida.

5. Catalisi eterogenea

Le reazioni catalitiche eterogenee implicano la diffusione dei componenti verso il catalizzatore, la rimozione dei prodotti di reazione dal catalizzatore e il trasferimento di calore. La reazione eterogenea si sviluppa, successivamente, in una regione ‛cinetica', dove la velocità di reazione è controllata dalla trasformazione chimica sulla superficie del catalizzatore, in una regione di ‛diffusione interna', dove il trasporto dei reagenti all'interno dei pori del catalizzatore costituisce lo stadio che controlla la velocità della reazione, e in una regione di ediffusione esterna', dove tale stadio è rappresentato dal trasferimento dei reagenti sulla superficie esterna del catalizzatore. La probabilità di transizione della reazione dalla regione cinetica a quella di diffusione aumenta con la temperatura e la pressione. Quando la reazione passa alla regione di diffusione interna, l'energia di attivazione dell'espressione di Arrhenius (da 10 a 40 kcal/mole per le reazioni catalitiche) diventa la metà di quella per la regione cinetica. La teoria di questo processo è stata sviluppata da Ja. B. Zel'dovi. Un coefficiente di temperatura ancora più basso si osserva per la regione di diffusione esterna, dove la dipendenza della velocità di reazione dalla temperatura diventa quella del coefficiente di diffusione.

Le reazioni nella regione cinetica sono sia quelle tra le molecole adsorbite, sia quelle tra le molecole adsorbite e le molecole derivate dalla fase gassosa. Nel primo caso la velocità di reazione è data dall'espressione

dove θ_A e θ_B sono le aree delle superfici occupate rispettivamente dalle molecole A e B. Queste quantità si determinano facendo uso dell'isoterma di Langmuir:

θ_A = b_A[A]/{l + b_A[A]}

θ_B = b_B[B]/{l + b_B[B]},

dove b_A (b_B) è il coefficiente di adsorbimento del composto A (B), che rappresenta il rapporto tra le costanti di velocità di adsorbimento e di deadsorbimento: b = k_a/k_d.

Il coefficiente b diminuisce con la temperatura secondo la relazione

b = b_c exp(Q/RT),

dove Q è il calore di adsorbimento per mole. Sostituendo θ nell'equazione della velocità di reazione, si possono ottenere reazioni di ordine zero, di primo o di secondo ordine, a seconda delle aree ricoperte.

Quando la reazione interessa molecole appartenenti a una fase gassosa, per esempio quando una sostanza A reagisce con una sostanza B adsorbita, l'equazione della velocità di reazione sarà data da

Queste equazioni sono valide per uno strato ideale adsorbito con siti catalitici uniformi, sempre che non vi siano interazioni tra le molecole adsorbite. Eventuali effetti di non uniformità complicano notevolmente le equazioni cinetiche.

In certi casi la reazione avviene per mezzo di composti intermedi attivi, quali radicali e ioni, e anche attraverso la formazione di complessi di superficie nei quali la sostanza adsorbita, quale può essere un atomo di un metallo di transizione, agisce da legante nella sfera di coordinazione del centro attivo.

La funzione svolta dai complessi intermedi attivi ha rivelato certi aspetti comuni alla catalisi eterogenea e a quella omogenea.

6. Reazioni in fase solida

Le reazioni in fase solida e quelle in fase liquida presentano molti aspetti comuni: specificatamente, la possibilità che la reazione si verifichi nella regione cinetica o in quella di diffusione (a seconda del valore del rapporto delle costanti di velocità), il cosiddetto effetto gabbia, l'effetto del mezzo (o della matrice solida) sulla velocità di reazione e così via.

Gli aspetti specifici delle reazioni in fase solida sono dovuti alla formazione di una fase separata da parte dei prodotti di reazione e ai difetti del reticolo cristallino, come le dislocazioni, che rendono la velocità di reazione considerevolmente più alta di quella che dovrebbe competere a un cristallo ideale.

La velocità di reazione al confine di questa fase, o vicino ad esso, è considerevolmente più alta, per molte ragioni che dipendono dalla natura della reazione. La reazione, originatasi nella zona di un difetto del cristallo, procede a causa dell'aumento del numero dei siti attivi e dell'accrescimento delle loro aree. Questo fatto dà ragione dell'aumento della velocità di reazione con la durata della trasformazione. Reazioni di questo tipo sono chiamate ‛topochimiche'.

La reazione chimica conduce ad un numero più grande di difetti (dislocazioni) e ciò, a sua volta, accelera la reazione: si produce una certa catena in cui i difetti del reticolo agiscono come siti attivi.

Il reticolo ordinato della sostanza iniziale dà ragione del verificarsi di processi cooperativi che interessano un vasto numero di molecole. In questo caso l'equazione di Arrhenius potrebbe non essere più valida.

Il reticolo ordinato può anche favorire una rapida polimerizzazione nella fase solida a bassa temperatura, purché la struttura cristallina del monomero sia simile a quella dei prodotti finali.

Certi tipi di strutture cristalline assicurano il trasferimento della valenza libera, secondo un meccanismo simile a quello del trasferimento successivo di protoni nell'acqua. Reazioni ‛tunnel' di trasferimento di elettroni e protoni sono possibili a basse temperature.

bibliografia

Bamford, C. H., Tipper, C. P. H. (a cura di), Comprehensive chemical kinetics, 3 voll., Amsterdam-London-New York 1969.

Benson, S. W., The foundations of chemical kinetics, New York-London 1960.

Emanuel, N. M., Denisov, E. T., Maizus, Z. K., Liquid-phase oxidation of hydrocarbons, New York 1967.

Kondrat′ev, V. N., Chemical kinetics of gas reactions, Oxford-London-New York-Paris 1964.

Laidler, K. J., Chemical kinetics, New York 1969.

Semenov, N. N., Chemical kinetics and chain reactions, Oxford 1935.

Semenov, N. N., Some problems of chemical kinetics and reactivity, Princeton 1959.