Apollonio, circonferenza di

Apollonio, circonferenza di

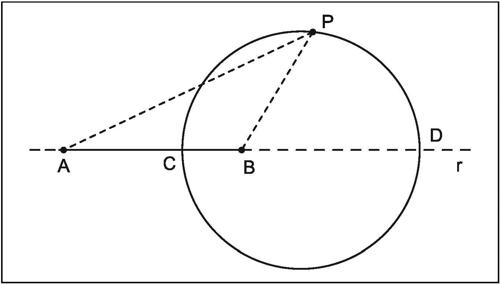
Apollonio, circonferenza di luogo geometrico dei punti del piano tali che il rapporto delle loro distanze da due punti fissati abbia un valore costante k ≠ 1. Fissati i punti A e B sulla retta r, i punti C e D sono tali che

cioè C e D dividono il segmento AB, rispettivamente internamente ed esternamente, in due parti il cui rapporto è k. È detta circonferenza d’Apollonio anche ogni circonferenza tangente a tre circonferenze assegnate. Il problema, noto anche come problema di Apollonio, della ricerca di una circonferenza tangente a tre circonferenze assegnate può ammettere fino a otto soluzioni e si traduce nella risoluzione di un sistema di 3 equazioni di secondo grado in tre incognite.