Malfatti, circonferenze di
Malfatti, circonferenze di
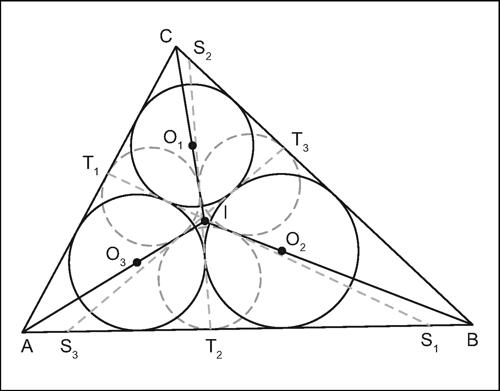
Malfatti, circonferenze di nella geometria del piano, sono così indicate le tre circonferenze interne a un triangolo che sono mutuamente tangenti tra loro e ognuna tangente a due lati del triangolo. Tali circonferenze furono indicate da G. Malfatti, nei primi anni del xix secolo, come soluzione di un problema, da lui stesso proposto e noto come marble problem (problema del marmo), consistente nel tracciare, internamente a un triangolo, tre circonferenze tali da racchiudere la massima area. Tale problema è anche noto come problema di → Malfatti. Per tracciare le tre circonferenze di Malfatti in un triangolo ABC si procede nel seguente modo:
• si individua l’incentro I del triangolo (intersezione delle sue bisettrici);
• si costruiscono le circonferenze inscritte nei triangoli AIC, AIB, BIC;
• per ciascuna coppia di circonferenze, si tracciano le due rette a esse tangenti (una delle quali è bisettrice);
• si determinano così tre quadrilateri aventi ognuno due lati sui lati del triangolo e gli altri due sulle coppie di tangenti tracciate;
• in ciascuno di tali quadrilateri è inscrivibile una circonferenza: le tre circonferenze così ottenute sono le circonferenze cercate.