circoscrivibilita

circoscrivibilita

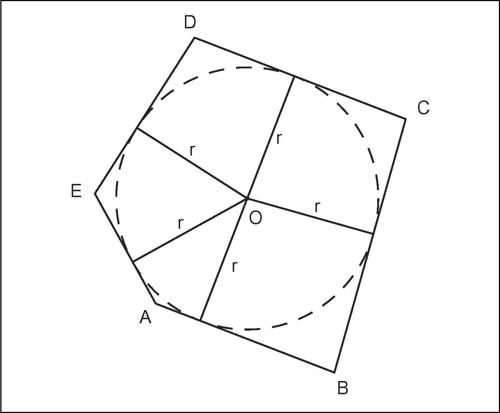
circoscrivibilità in geometria, proprietà di una figura piana che consiste nella possibilità di tracciare attorno a essa una linea chiusa (poligonale, circonferenza, ellisse ecc.) che passa per particolari punti del suo contorno. Un poligono è circoscrivibile se esiste una linea chiusa (una circonferenza se non viene diversamente specificato) che passa per tutti i suoi vertici. Un poligono è circoscrivibile (mediante una circonferenza) se e solo se gli assi dei lati del poligono passano tutti per uno stesso punto (circocentro). Sono circoscrivibili tutti i triangoli, tutti i quadrilateri aventi gli angoli opposti supplementari, tutti i poligoni regolari. Non tutti i poligoni con più di tre lati risultano però circoscrivibili. Non lo sono, per esempio, i trapezi rettangoli, mentre lo sono i rettangoli. Una circonferenza può essere circoscrivibile mediante un poligono, i cui lati risultano tangenti alla circonferenza. In questo caso si dice che il poligono è circoscritto alla circonferenza. In un poligono circoscritto a una circonferenza tutte le bisettrici passano per uno stesso punto (incentro). Un quadrilatero circoscritto a una circonferenza ha la proprietà di avere costante la somma dei lati opposti. L’area di un poligono circoscritto a una circonferenza di raggio r è data dal prodotto del semiperimetro per il raggio, ovvero A = pr, avendo indicato con p il semiperimetro del poligono. La nozione di circoscrivibilità è strettamente connessa con quella di → inscrivibilità.