cissoide
cissoide
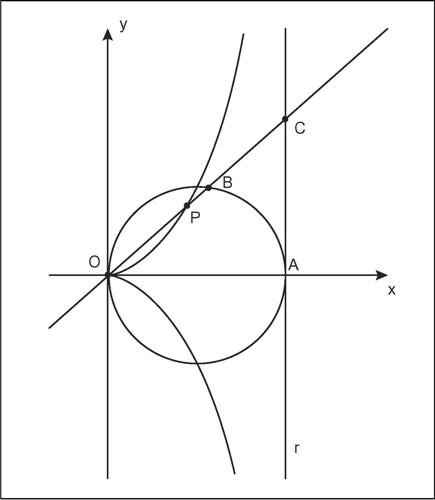
cissoide curva algebrica piana del terzo ordine, generata nel modo che segue. Date una circonferenza γ di diametro OA e una retta r tangente a essa in A e dette B e C rispettivamente le intersezioni di una retta per O con γ e r, la cissoide è il luogo dei punti P, tali che OP = BC, descritto dalla retta nella sua rotazione attorno a O. In un sistema di riferimento con origine in O e asse parallelo a r, indicando con a il raggio della circonferenza base, la cissoide ha equazione cartesiana
ed equazione polare ρ = 2atanθsinθ, con –π/2 < θ ≤ π/2. Da un punto di vista algebrico, la cissoide è una cubica razionale, dotata di cuspide nell’origine, con tangente l’asse x, retta rispetto alla quale risulta simmetrica. La retta r, di equazione x = 2a, risulta asintoto verticale. L’area compresa tra la cissoide e l’asintoto è 3πa2.
La cissoide fu studiata dal matematico greco Diocle (secc. ii-i a.C.) per risolvere il problema di Delo o della duplicazione del → cubo, e pertanto è detta anche cissoide di Diocle.