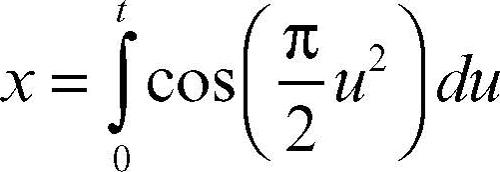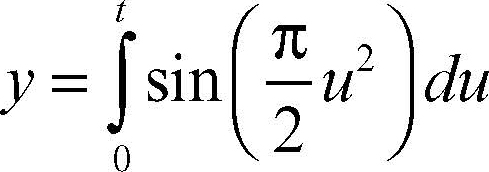clotoide

Enciclopedia della Matematica (2013)

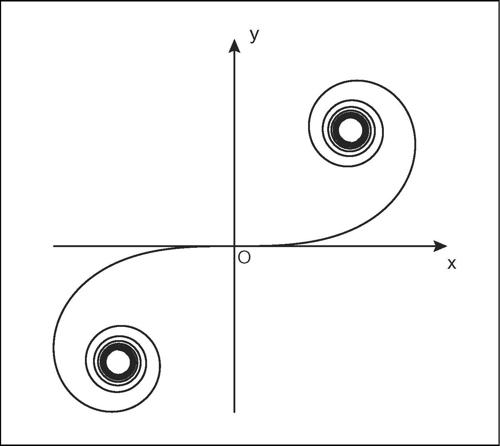
clotoide


clotoide o spirale di Cornu, curva piana trascendente, luogo geometrico dei punti per i quali è costante il prodotto fra raggio di curvatura e lunghezza dell’arco misurata da un’origine fissa. La clotoide è costituita da due spirali simmetriche rispetto all’origine, tendenti a due punti asintotici. Le equazioni parametriche della clotoide sono date dai cosiddetti integrali di Fresnel:

formula
formula

La clotoide trova applicazione nella costruzione di strade e ferrovie, in quanto costituisce il raccordo più funzionale tra un percorso rettilineo e un percorso circolare, poiché lungo l’arco di clotoide l’accelerazione centripeta passa da zero (sul percorso rettilineo) al valore massimo (in curva) variando linearmente nel tempo. Trova applicazione anche nello studio della diffrazione della luce. Il termine «clotoide» fu attribuito alla curva, agli inizi del Novecento, da E. Cesàro, con riferimento alla parca Cloto che filava lo stame della vita.

CLOTOIDE

Vedi anche
strada Striscia di terreno più o meno lunga e di sezione sensibilmente costante, attrezzata per il transito di persone e di veicoli (in qualche caso di sole persone, s. pedonale) sia nei centri abitati sia nelle campagne. Il termine ha valore generico che può indicare sia passaggi lunghi pochi metri, come alcune ... Parche (lat. Parcae) Divinità della mitologia classica. In origine, presso i Latini antichi si ebbe una sola P., dea che presiedeva alle nascite, poi se ne ebbero tre, assimilate alle Moire greche, divinità che presiedevano al destino dell’uomo dalla nascita alla morte.
Tag
Altri risultati per clotoide
  • clotoide
    Enciclopedia on line
    Curva piana (anche detta spirale c.), non algebrica, simmetrica rispetto a un punto O (v. fig.) e dotata di due punti asintotici A e A′ (ai quali cioè la curva si avvicina indefinitamente, con andamento a spirale, senza raggiungerli mai); in ogni punto della c. la curvatura 1/r è proporzionale alla ...
  • clotoide
    Dizionario delle Scienze Fisiche (1996)
    clotòide [Der. del gr. klótho "filare", con allusione all'avvolgersi del filo sulla rocca della filatrice, come fa questa curva intorno ai suoi punti asintotici] [ALG] Curva piana, detta anche spirale c., non algebrica, simmetrica rispetto a un punto O (v. fig.), caratterizzata dal fatto che in ogni ...
  • CLOTOIDE
    Enciclopedia Italiana (1931)
    È la curva piana, risolutrice del seguente problema, proposto da Giacomo Bernoulli: Trovare una curva tale, che in un suo qualsiasi punto la curvatura sia inversamente proporzionale all'arco contato da una origine fissa. In coordinate cartesiane ortogonali si può rappresentare per mezzo delle equazioni ...
Vocabolario
clotòide
clotoide clotòide s. f. [comp. del gr. κλώϑω «filare» (per allusione al doppio avvolgimento intorno alla rocca e al fuso) e -oide]. – In geometria, curva piana (anche detta spirale c.), non algebrica, simmetrica rispetto a un punto O e...
radiòide
radioide radiòide s. m. [comp. di radi03 e -oide]. – Denominazione che si dà, nella tecnica, alle curve piane che soddisfano a particolari condizioni (di solito la relazione di proporzionalità inversa) imposte al raggio di curvatura in...