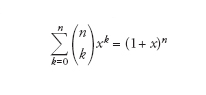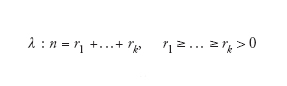Combinatoria

Combinatoria

Secondo alcuni la combinatoria costituisce soltanto una parte della matematica, secondo altri non rappresenta una branca separata dalle altre ma le pervade tutte, poiché la maggioranza dei matematici si occupa almeno in parte di essa. Anche chi se ne interessa sente spesso il bisogno di dissimulare il proprio lavoro, definendolo una semplice soluzione di rompicapi. Jean Dieudonné, portavoce del gruppo Bourbaki, con un misto di scetticismo e di imbarazzo affermava che non era ancora chiaro quale fosse il legame tra la combinatoria e la matematica concettuale.

Eppure, il primo approccio di Leonhard Euler alla topologia fu la risoluzione del problema dell'esistenza di un cammino che attraversasse i ponti della città di Königsberg una sola volta. A lui si deve anche l'origine dello studio dei quadrati latini, nella forma del cosiddetto problema degli ufficiali: "Dati trentasei ufficiali di sei gradi diversi e di sei reggimenti diversi, uno per ogni grado e reggimento, è possibile sistemare i trentasei ufficiali in un quadrato 6×6 in modo che in ogni riga e colonna vi sia uno e un solo ufficiale per ogni grado e reggimento?". Euler sospettava che la risposta fosse negativa, e che lo stesso dovesse accadere se invece di 6 si fosse preso un qualunque "numero non parimenti pari" (cioè un numero congruo a 2 mod 4), mentre sapeva che era positiva in tutti gli altri casi. La prima parte della congettura era vera, come fu stabilito da Gaston Tarry con un'analisi dettagliata di tutti i casi possibili, la seconda invece fu dimostrata falsa da Raj C. Bose, Sharad S. Shrikhande ed E.T. Parker nel 1960.

Nel XIX sec. Thomas P. Kirkman diede inizio alla teoria dei disegni con il problema delle collegiali: "Quindici collegiali escono tre alla volta per sette giorni di seguito. Si chiede di redigere un calendario in modo tale che due qualunque di esse non escano mai insieme due volte". Come per sottolinearne la natura frivola, il problema fu pubblicato nel "Lady's and Gentleman's Diary" nel 1850. Kirkman stesso risolse il problema, e il fatto che un qualunque numero di ragazze congruo a 3 mod 6 andasse bene richiamò l'attenzione di molti. I risultati furono riassunti nelle numerose edizioni dei Mathematical recreations and essays di Walter W. Rouse Ball, ma per la soluzione definitiva si dovette attendere l'opera di Dijen Ray-Chaudhuri e Richard Wilson pubblicata nel 1971.

Un altro esempio della confusione sulla natura e la destinazione dei risultati di combinatoria si ebbe quando Arthur Cayley pubblicò nel 1879 un articolo nel quale veniva ravvivato l'interesse per il problema dei quattro colori. L'articolo uscì nei "Proceedings of the Royal Geographical Society", malgrado i geografi non avessero mai mostrato un particolare interesse per il numero minimo di colori da usare nelle loro mappe (il problema, sollevato da Francis Guthrie intorno al 1850, chiede di sapere se, data una qualunque carta geografica, sia possibile campire le regioni con quattro colori in modo tale che regioni adiacenti abbiano colori diversi).

Nel corso del XX sec. la combinatoria cominciò però a trovare un proprio posto nella matematica tradizionale. Godfrey H. Hardy e John E. Littlewood studiarono il comportamento asintotico del numero p(n) di partizioni di un intero n (le partizioni di n sono i modi di scrivere n come somma di interi positivi, senza tenere conto dell'ordine). Il legame fondamentale tra problemi di conteggio di oggetti e l'analisi è dato dalle serie formali di potenze, i coefficienti delle quali sono appunto i numeri che contano gli oggetti in considerazione; le idee fondamentali risalgono, anche in questo caso, a Euler.

Problemi collegati con quello degli ufficiali o con quello di Kirkman nacquero indipendentemente in statistica, dove Ronald A. Fisher e Frank Yates svilupparono la teoria della progettazione degli esperimenti. A Calcutta, Bose diede notevole impulso allo sviluppo delle geometrie finite (l'analogo delle classiche geometria proiettiva e geometria polare su campi finiti). Sviluppi in altri campi, come quello della costruzione dei gruppi semplici finiti e quello della geometria algebrica, spingevano nella stessa direzione. Le geometrie finite, che da qui presero spunto per poi crescere velocemente grazie anche ai lavori pionieristici di Beniamino Segre, costituiscono oggi una parte fiorente della combinatoria.

Con l'avanzare del secolo si assiste a un'accelerazione di tale tendenza; sviluppi più recenti saranno presi in considerazione nella nostra esposizione. n

L'oggetto della combinatoria

La combinatoria è notoriamente difficile da caratterizzare. Numerosi matematici, che non si definirebbero come studiosi di combinatoria, nelle loro ricerche fanno uso di idee e tecniche combinatorie. In termini molto generali il problema fondamentale della combinatoria è quello di stabilire se sia possibile o meno una data disposizione di oggetti secondo determinate regole (come per gli ufficiali di Euler o le ragazze di Kirkman). A una domanda di questo tipo si può rispondere sia esibendo una costruzione esplicita, sia con una dimostrazione di non esistenza; più raro è trovare una dimostrazione di esistenza non costruttiva (che può giovarsi, per es., di tecniche probabilistiche). Se la disposizione richiesta è possibile, ci si può chiedere in quanti modi si può ottenere (di solito a meno di una equivalenza che deve essere specificata con precisione). È possibile che, se il numero dei modi è grande, non si sia in grado di trovare una formula esatta per esprimerlo e ci si debba accontentare di una formula approssimata. Un'altra tecnica utile è quella di un algoritmo per costruire le disposizioni (o anche di un algoritmo casuale che scelga una delle molte disposizioni esistenti).

tab. 1

Per fissare le idee consideriamo il problema fondamentale delle permutazioni e combinazioni. Abbiamo un insieme di n oggetti, diciamo a₁,a₂,…,a_n; ne vogliamo scegliere k. In quanti modi si può fare? Occorre naturalmente essere più precisi nel formulare il problema. Conta l'ordine nel quale vengono fatte le scelte? Possiamo scegliere uno stesso oggetto più di una volta? Le risposte sono contenute nella tab. 1.

Qui ⁿP_k=n(n−1)…(n−k+1) (il prodotto di k fattori a partire da n, ciascuno inferiore di uno a quello che lo precede), e ⁿC_k=ⁿP_k/k! (dove k! è il prodotto degli interi da 1 a k, cioè il numero delle permutazioni, od ordinamenti, di k oggetti). Le lettere P e C significano rispettivamente permutazioni (scelte ordinate) e combinazioni (scelte non ordinate). ⁿC_k ci dice quanti sottoinsiemi di cardinalità k sono contenuti nell'insieme di cardinalità n; il numero

[1]  formula.

Una funzione generatrice per questi numeri è

[2] formula

una forma del teorema del binomio (per esponenti interi positivi).

Consideriamo ora un problema più complicato. In quanti modi si possono ripartire i sottoinsiemi con k elementi di un insieme con n elementi, in modo che ciascuna parte consti di n/k sottoinsiemi che ricoprono tutti gli elementi dell'insieme di partenza (si suppone che k divida n)? Il fatto che una tale partizione sia possibile non è affatto ovvio ed è stato dimostrato da Zsolt Baranyai nel 1975. Per k=2 l'esistenza è immediata (è il problema di stilare un calendario di n⁻¹ partite per un torneo a n squadre in cui ogni coppia di squadre si incontra una sola volta). C'è una stima asintotica grossolana per il numero dei modi, ma per k>2 non si sa quasi nulla su questo numero.

Oltre a contare particolari oggetti (come, per es., famiglie di insiemi, grafi, insiemi ordinati, ecc.), la combinatoria enumerativa comprende anche tecniche di analisi per la determinazione di valori asintotici approssimati di funzioni che servono a contare. Un classico esempio è rappresentato dalla formula di Stirling, secondo la quale n! è uguale approssimativamente a (n/e)n√(2πn) per grandi valori di n (il rapporto delle due quantità tende a 1).

L'esatta enumerazione di oggetti combinatori si presta bene a essere trattata con tecniche algebriche, comprese serie formali, azioni di gruppi e lo studio delle algebre di incidenza di insiemi parzialmente ordinati. Ma l'algebra compare in combinatoria in molti altri modi. Per esempio gli schemi di associazione (una classe di oggetti combinatori scoperti indipendentemente in statistica, nei gruppi di permutazioni e negli algoritmi per l'isomorfismo dei grafi) sono essenzialmente la stessa cosa delle algebre di matrici reali simmetriche che ammettono una base di matrici a elementi 0 e 1, compresa la matrice identica, e la cui somma è la matrice con tutti 1. La teoria delle rappresentazioni di queste algebre ha un'importanza cruciale in combinatoria.

La teoria dei disegni riguarda disposizioni di sottoinsiemi di un insieme, o di lettere in uno schema di qualche tipo. Gli ufficiali di Euler e le collegiali di Kirkman sono prototipi dei problemi di questa area.

La combinatoria estremale si presenta generalmente in situazioni nelle quali una disposizione di un qualche tipo non è possibile. Per esempio, in un semplice problema considerato per primo da Kirkman ci si chiede se sia possibile scegliere un insieme di sottoinsiemi con tre elementi dell'insieme {1,…,n} in modo che due elementi qualunque compaiano simultaneamente in uno dei sottoinsiemi scelti (si tratta del problema delle collegiali senza la richiesta che le ragazze debbano camminare in fila per tre in cinque righe). Kirkman dimostrò che una soluzione è possibile se e soltanto se n è congruo a 1 o 3 mod 6; un insieme soluzione contiene esattamente n(n⁻¹)/6 terne. Per i valori di n per i quali non vi sono soluzioni ci si possono porre le seguenti domande: qual è il massimo numero di terne tale che due elementi qualunque capitino insieme al più una volta? Qual è il minimo numero di terne tale che due qualunque elementi capitino insieme almeno una volta? La prima domanda pone un problema di packing (impacchettamento), la seconda un problema di covering (ricoprimento). Entrambe fanno parte della combinatoria estremale.

La teoria dei grafi è leggermente diversa. Anche se sono stati scritti più lavori su essa che su tutto il resto della combinatoria, un grafo resta comunque una struttura combinatoria molto particolare. Un grafo consta di un insieme di vertici, alcune coppie dei quali sono congiunte da spigoli. Vi sono numerose varianti: gli spigoli possono essere orientati, uno spigolo può congiungere un vertice con se stesso, la stessa coppia di vertici può essere congiunta da più spigoli, ecc. Tale flessibilità permette ai grafi di avere applicazioni a situazioni di tipo molto vario. Nella teoria dei grafi si possono distinguere due argomenti principali: la connessione, che comporta la considerazione di cammini a più passi che congiungono coppie di vertici, e le colorazioni. In questo caso si colorano i vertici richiedendo che siano di colore diverso se congiunti da uno spigolo, oppure si colorano gli spigoli imponendo che siano di colore diverso se incidenti a uno stesso vertice.

I problemi di connessione sono ovviamente rilevanti in questioni riguardanti flussi su reti, problemi su vertici o spigoli dominanti, ecc., mentre i problemi di colorazione nascono quando il grafo rappresenta situazioni di incompatibilità (per es., in una serie di radio trasmettitori, per evitare interferenze, trasmettitori vicini devono usare frequenze diverse: quante frequenze sono allora necessarie?). Il problema più famoso è però quello dei quattro colori: è possibile campire una qualunque carta geografica facendo uso, appunto, di quattro colori, in modo tale che regioni confinanti abbiano tinte differenti? Si possono considerare le regioni come i vertici di un grafo e due vertici come congiunti da uno spigolo se le regioni corrispondenti hanno un confine comune.

Un tipo di oggetto combinatorio che supera queste divisioni è il matroide, inventato da Hassler Whitney per descrivere la nozione di indipendenza di un insieme di vettori di uno spazio vettoriale. Anche un grafo dà origine a un matroide: insiemi di spigoli aciclici (foreste) giocano il ruolo di insiemi indipendenti. Altri esempi provengono dalle trasversali di famiglie di insiemi. A un matroide è associato il suo polinomio di Tutte, che registra molte informazioni di carattere numerico sul matroide o sul grafo (compreso il numero delle colorazioni e dei flussi). Essi sono stati poi generalizzati nei matroidi di Coxeter, collegati ai gruppi di Coxeter come i matroidi lo sono al gruppo simmetrico.

Un altro principio unificante che supera le frontiere tra i diversi campi è la teoria di Ramsey, che Theodore Motzkin riassume nella frase "un completo disordine è impossibile". È caratteristico dei risultati di tale teoria affermare che un oggetto arbitrario contiene al proprio interno un oggetto molto più strutturato di quello di partenza. Per esempio, date sei persone a una festa, ve ne sono tre che si conoscono oppure tre che sono estranee l'una all'altra. Più in generale, se i k-sottoinsiemi (sottoinsiemi contenenti k elementi) di un insieme con n elementi sono colorati con r colori, allora (purché n sia sufficientemente grande, per es., esiste un l-sottoinsieme con tutti i k-sottoinsiemi dello stesso colore. Più in generale ancora, gli insiemi si possono sostituire con strutture matematiche di vario tipo.

Il problema è in questo caso quello di determinare gli opportuni numeri di Ramsey, come il precedente numero R(k, l, r). Maggiorazioni per questo numero seguono di solito dalla dimostrazione del teorema; le minorazioni richiedono una costruzione (nel caso preso in esame, cinque persone non bastano: un pentagono rosso con un pentagono blu stellato inscritto non ha triangoli monocromatici). Un'importante tecnica, che Paul Erdös ha ideato per questo problema ma che ha applicabilità molto più ampia, è il metodo probabilistico. Per trovare una minorazione per R(2, l,2) si prenda un insieme di n punti e a caso si colorino le coppie di rosso e di blu. Non è difficile calcolare il numero atteso degli l-sottoinsiemi monocromatici. Se n〈2l, questo numero è minore di 1 e vi deve quindi essere una colorazione senza l-sottoinsiemi monocromatici. Se ne conclude che R(2, l, 2)≥2^l/2-. Si tratta di un buon esempio di una dimostrazione di esistenza non costruttiva: ci dice che la colorazione richiesta esiste, ma non dà alcun suggerimento su come costruirne una.

Rapporti con la scienza e la società

È nostra convinzione che uno dei fattori principali che hanno favorito la crescita e l'accettazione della combinatoria provenga da ambiti esterni alla matematica.

Nel corso della storia, alcuni hanno pensato che il mondo fosse infinitamente divisibile, altri hanno aderito a qualche forma di teoria atomica. Nel rapido sviluppo della matematica nel XVIII e XIX sec., il punto di vista del continuo ha avuto il predominio. A seguito dello sviluppo del calcolo differenziale e integrale di Isaac Newton e Gottfried W. Leibniz, sembrò che il mondo si potesse comprendere utilizzando tecniche analitiche come le equazioni differenziali. Le formulazioni della meccanica di Joseph-Louis Lagrange e William R. Hamilton, le equazioni di Maxwell per l'elettromagnetismo e l'equazione di Laplace sembravano parlare di un mondo continuo che l'analisi poteva far comprendere nel modo migliore. Uno dei primi segni di cambiamento si ebbe con il crescere di applicazioni della matematica nelle quali la rilevanza dell'analisi non era così evidente. Durante la Seconda guerra mondiale John von Neumann e Oskar Morgenstern svilupparono la teoria dei giochi, una descrizione di come si debba reagire in circostanze imprevedibili. Nella prefazione a Theory of games and economic behavior, essi scrivono: "L'importanza dei metodi matematici sembra spostarsi verso la combinatoria e la teoria degli insiemi, e allontanarsi dall'algoritmo delle equazioni differenziali che domina la fisica matematica". Strettamente connesso a tutto ciò è lo sviluppo della ricerca operativa, una disciplina che ha sempre avuto stretti legami con la combinatoria.

Un altro elemento provenne, con la nascita della meccanica quantistica, proprio dalla roccaforte di quell'"algoritmo delle equazioni differenziali". Max Planck e Albert Einstein scoprirono che nei processi subatomici l'energia non può fluire con continuità; essa si può trasportare soltanto in pacchetti chiamati quanti; analogamente, lo stato di un elettrone che orbita attorno a un nucleo atomico è descritto da quattro numeri quantici discreti. Il principio di esclusione di Pauli afferma che due elettroni non possono avere gli stessi quattro numeri quantici e una transizione tra stati distinti provoca l'assorbimento o il rilascio di multipli interi di una quantità fissa di energia: si spiegano in tal modo le linee spettrali discrete che caratterizzano gli atomi.

Più recentemente alcuni fisici, in particolare Lee Smolin e Rafael Sorkin, hanno suggerito che lo spazio-tempo è esso stesso discreto: assomiglia più a una rete che a una varietà continua, se studiato su piccola scala, paragonabile alla lunghezza di Planck. Tale lunghezza è talmente ridotta che, nella scala alla quale noi possiamo effettuare misurazioni, questa natura discreta non è osservabile ed è per questo che le equazioni differenziali danno una buona descrizione dell'Universo. La geometria non commutativa, sviluppata da Alain Connes e altri, è anch'essa legata alla quantizzazione dello spazio-tempo.

Dalla biologia proviene la consapevolezza che anche il linguaggio dei geni è discreto. Una molecola di DNA si può descrivere come una lunga sequenza di simboli su un alfabeto di quattro lettere (le quattro basi, adenina, citosina, guanina e timina). Una sequenza di tre lettere codifica uno dei venti amminoacidi, assemblati in proteine che regolano tutti i processi che hanno luogo in un organismo vivente.

Non possiamo terminare questo paragrafo senza menzionare la straordinaria influenza del matematico ungherese Paul Erdös. Le sue conoscenze matematiche erano vastissime: iniziò con la teoria dei numeri, lavorando anche in analisi e teoria degli insiemi, ma al centro dei suoi interessi era la combinatoria. Passò gran parte della vita senza avere una fissa dimora, viaggiando per il mondo e collaborando con centinaia di matematici. Negli anni precedenti all'invenzione della posta elettronica egli contribuì notevolmente alla comunicazione tra studiosi dell'Est e dell'Ovest; ha ispirato un vasto corpus di ricerche (i suoi 1500 lavori oscurano la produzione di ogni altro matematico tra i moderni).

La combinatoria e il computer

Le relazioni tra combinatoria e computer sono molto strette, e ognuno dei due settori di ricerca influenza l'altro. Intanto, il computer ha avuto in combinatoria un impatto maggiore che in altre parti della matematica, perché è in grado di compiere lunghe analisi, caso per caso, evitando l'errore umano. Nel 1977 Kenneth Appel e Wolfgang Haken annunciarono la dimostrazione della congettura dei quattro colori con l'aiuto del computer. Tale dimostrazione è interattiva: i matematici e il computer si dividono il compito di generare e controllare le circa 2000 configurazioni da considerare. L'annuncio provocò una grande agitazione. Alcuni pensavano che una dimostrazione del genere non potesse essere considerata tale. Thomas Tymoczko sostenne questa tesi con l'argomento che non era possibile per un essere umano esaminarla, mentre Edward R. Swart si schierò sul fronte opposto. In ogni caso la controversia concentrò l'attenzione sul problema di cosa sia una dimostrazione. La storia ha un risvolto ironico: in una nuova prova del teorema dovuta a Neil Robertson, Daniel P. Sanders, Paul D. Seymour e Robin Thomas, gli autori sostituiscono il procedimento a mano con il computer perché più affidabile dell'uomo!

In seguito si assisterà a teoremi di combinatoria stabiliti mediante calcoli al computer ancora più lunghi. Clement W.H. Lam e i suoi collaboratori hanno dimostrato la non esistenza di un piano proiettivo di ordine 10 con un programma che ha girato per molti anni (suddiviso in vari casi: per quelli difficili un computer Cray lavorava in background, per i più facili si usava un microcomputer).

Nella direzione opposta, l'informatica è stata una ricca fonte di ispirazione e di problemi per la combinatoria. Anche prima della costruzione dei computer, questioni di carattere teorico hanno portato a risultati importanti. Kurt Gödel nel 1931 dimostrò che vi sono enunciati veri sui numeri naturali che non si possono dedurre dagli assiomi di un sistema standard come quello di Peano. Tale risultato ebbe un grande significato per i fondamenti della matematica, ma l'enunciato non dimostrabile di Gödel non aveva un significato matematico diretto. Il primo esempio di enunciato di carattere matematico non dimostrabile nell'aritmetica di Peano fu scoperto da Jeff Paris e Leo Harrington e si tratta di un problema di combinatoria. Tale enunciato non è dimostrabile a partire dagli assiomi in quanto la corrispondente funzione di Paris-Harrington cresce più rapidamente di ogni funzione calcolabile. Sono stati scoperti numerosi altri esempi di questo fenomeno, la maggior parte di natura combinatoria.

Più recentemente l'attenzione si è spostata dalla calcolabilità alla complessità di calcolo: se qualcosa è calcolabile, ci si chiede quali risorse (tempo, memoria, ecc.) sono necessarie per tale calcolo. Una classe di problemi si dice calcolabile in tempo polinomiale, o in P, se ognuno di essi è risolvibile in un numero di passi maggiorato da un polinomio nelle dimensioni dell'input. Una classe è in NP se si ha lo stesso risultato ammettendo un certo numero di tentativi di indovinare il risultato (o, ciò che è lo stesso, se una soluzione proposta si può controllare in un numero polinomiale di passi). Il grande problema irrisolto della teoria della complessità chiede di sapere se P è uguale a NP. Si tratta di un problema importante per la combinatoria perché è noto che molti problemi intrattabili (tra cui quello dell'esistenza di un ciclo hamiltoniano in un grafo) sono in NP. Nel caso ‒ improbabile ‒ di una soluzione positiva, vi sarebbero algoritmi veloci per tutti questi problemi.

Tendenze e problemi

Per avere una misura delle connessioni tra la combinatoria e altre parti della matematica ci riferiamo alla Math-ematical Subject Classification. Essa mostra rinvii dalla combinatoria alla logica matematica e ai fondamenti (calcolabilità e teoria della ricorsività), a ordini, reticoli, strutture algebriche ordinate (aspetti algebrici degli insiemi parzialmente ordinati), alla teoria dei numeri (successioni e insiemi, geometria dei numeri, partizioni, campi finiti e anelli), alla teoria dei gruppi e sue generalizzazioni (rappresentazioni, teoria geometrica dei gruppi), alle funzioni speciali (funzioni ipergeometriche e funzioni ipergeometriche fondamentali), alla geometria (sistemi di chiusura geometrica, geometrie finite e particolari strutture di incidenza), alla geometria convessa e discreta (politopi e poliedri), alla topologia in basse dimensioni (nodi e concatenazioni in S³), alla statistica (progettazione di esperimenti), all'informatica (matematica discreta, algoritmi), alla ricerca operativa (programmazione matematica), a informazione e comunicazione (circuiti).

Molte delle tendenze più interessanti della moderna combinatoria sono strettamente legate ad altre parti della matematica, e non possono esserne separate facilmente. Per esempio, molti pensano che uno degli sviluppi tecnologici che avranno luogo in questo secolo interesserà la computazione quantistica. Al momento, la teoria è molto più avanti delle applicazioni. Si sa che, se sarà costruito, un computer quantistico potrà risolvere efficientemente problemi come la fattorizzazione di interi molto grandi e il problema del logaritmo discreto. Ciò è di grande interesse perché questi due problemi sono fondamentali per la sicurezza dei notissimi codici a chiave pubblica RSA e El-Gamal; la sicurezza di tali codici sarebbe notevolmente compromessa se i computer quantistici fossero effettivamente costruiti.

È stato recentemente dimostrato da Michael H. Freedman, Alexei Kitaev, Michael Larsen, Robert Solovay e Zhengang Wang che la parte quantistica di ogni computazione appunto quantistica può essere sostituita da un singolo calcolo del polinomio di Jones di una certa treccia in una particolare radice dell'unità. Il polinomio di Jones è un caso particolare del polinomio di Tutte di un matroide; la complessità di calcolo del polinomio di Tutte è stata studiata da Dominique Welsh e altri.

Più in generale ‒ si pensi per esempio al lavoro di Richard E. Borcherds ‒ molte identità combinatorie sono state interpretate come formule del denominatore o formule dei caratteri di Weyl per algebre di Lie o per oggetti algebrici a esse connessi (superalgebre di Lie, algebre di Kac-Moody).

Inoltre, in combinatoria algebrica una vecchia idea è ancora attivamente oggetto di studio. Le rappresentazioni irriducibili del gruppo simmetrico S_n sono etichettate dalle partizioni di n, e regole combinatorie danno informazioni sulle rappresentazioni. L'esempio più semplice è la dimensione. Data una partizione

[3] formula

vi sono due espressioni per il grado f_λ della corrispondente rappresentazione irriducibile. Ciascuna è definita in termini del diagramma della partizione, che ha k righe con ri caselle nella i-esima riga (allineate a sinistra). La prima formula afferma che f_λ è uguale a n! diviso il prodotto delle lunghezze dei 'ganci' delle celle nel diagramma, dove un gancio consta di una cella e di quelle che si trovano o sotto di essa nella stessa colonna o alla sua destra nella stessa riga. La seconda formula afferma che fλ è uguale al numero delle tavole di Young associate al diagramma, dove una tavola di Young è un'assegnazione dei numeri 1,…,n alle celle tale che i numeri siano decrescenti lungo ogni colonna e lungo ogni riga.

Molti altri parametri della teoria delle rappresentazioni si possono calcolare attraverso una simile combinatoria. Mediante l'impiego di metodi che risalgono a Hermann Weyl si possono anche ottenere informazioni sulle rappresentazioni dei gruppi di Lie classici.

Più interessante è la situazione per le rappresentazioni in caratteristica diversa da zero. Le rappresentazioni non sono ora sempre semisemplici, e una rappresentazione indecomponibile può avere una struttura di sottomoduli molto complicata. Ancora una volta vi sono regole combinatorie che danno informazioni, in generale riducendo gli elementi che entrano nelle tavole.

Un altro legame del tutto inatteso è dato dalla nuova dimostrazione del teorema di Szemerédi (secondo cui ogni insieme di numeri naturali con densità superiore positiva contiene progressioni aritmetiche arbitrariamente lunghe) per la quale Harry Furstenberg ha utilizzato metodi di teoria ergodica. Ciò ha portato a un incontro molto ravvicinato tra combinatoria e teoria ergodica, nel quale una arricchisce l'altra. La teoria ergodica studia le iterazioni di trasformazioni di spazi di misura; un caso importante è quello in cui lo spazio consta di funzioni sui naturali o sugli interi e la trasformazione è indotta da uno shift. Le iterazioni dello shift descrivono efficacemente la combinatoria dei naturali.

Interazioni come queste, con linee di confine che si incrociano, sono per loro natura imprevedibili; tuttavia le direzioni della ricerca nell'ambito della combinatoria sono forse un po' più facili da immaginare. Vediamone alcune.

Colorazioni di grafi. Vi sono due problemi principali, uno per la colorazione di vertici (congettura di Hadwiger), l'altro di spigoli (congettura della colorazione per liste). La congettura di Hadwiger: un grafo i cui vertici non si possono colorare con meno di n colori (in modo che vertici adiacenti abbiano colori diversi) contiene il grafo completo K_n come minore (si osservi che in caso positivo si avrebbe una generalizzazione del teorema dei quattro colori, perché è noto che un grafo planare non può avere K₅ come minore). La congettura della colorazione per liste: supponiamo che gli spigoli di un grafo si possano colorare con n colori in modo che due spigoli incidenti a uno stesso vertice non abbiano mai lo stesso colore. Allora, assegnata una lista L(s) di colori per ogni spigolo s (scelti da un insieme arbitrariamente grande di colori, ma contenente soltanto n colori), è possibile colorare ogni spigolo con un colore della lista in modo che la condizione sugli spigoli incidenti continui a valere (la congettura analoga per colorazioni dei vertici è falsa).

Minori. I minori dei grafi si generalizzano in modo naturale ai matroidi; c'è quindi molto lavoro da fare per generalizzare i risultati di Neil Robertson e Paul Seymour! Vi sono anche alcuni nuovi e interessanti invarianti minori-monotoni, tra i quali uno scoperto da Yves Colin de Verdière, che ha dato luogo a risultati e congetture interessanti, compreso un criterio che stabilisce condizioni in base alle quali un grafo si possa immergere in ℝ3 senza che mai due circuiti siano intrecciati.

Teoria dei disegni. In tale campo di ricerca sono stati formulati problemi molto difficili. Generalizzando la definizione di Kirkman, un sistema di Steiner S(t,k,v) consta di un insieme di blocchi, o k-sottoinsiemi di un insieme di v punti, tali che t punti qualunque appartengano a un unico blocco. Per escludere casi banali supponiamo v problemi elencati di seguito sono aperti. (a) Esiste un sistema di Steiner S(t,k,v) con t ≥6? (b) Un piano proiettivo di ordine n è un sistema di Steiner S(2,n+1,n ²+n+1). Esiste un piano proiettivo di ordine che non sia una potenza di un numero primo? (Un esempio di ordine n, se n è una potenza di un primo, si costruisce facilmente a partire dal campo finito di ordine n).

Jacques Hadamard aveva dimostrato che una matrice na elementi che soddisfano ∣a_ij∣≤1 per ogni i, j ha determinante al più nⁿ in valore assoluto, con uguaglianza se e solo se tutti gli elementi sono uguali a ±1 e AA^T=nI. Una matrice che verifichi queste due condizioni si chiama matrice di Hadamard. L'ordine n di una tale matrice, se è maggiore di 2, deve essere multiplo di 4. Una congettura afferma inoltre che esistono matrici di Hadamard per tutti gli ordini divisibili per 4.

Enumerazione. È noto che alcune classi di strutture sono difficili da contare. Alcuni esempi sono: quadrati latini, spazi lineari, poliomini, politopi, nodi. Inoltre, quanti elementi contiene il reticolo distributivo libero con n generatori? (È lo stesso numero delle famiglie di sottoinsiemi di un insieme di n elementi i cui membri sono a due a due non confrontabili rispetto all'inclusione).

Numeri di Ramsey. Il problema di trovare valori esatti per i numeri di Ramsey classici Rè uno dei più difficili della combinatoria e solo pochi valori sono noti.

Bibliografia

Appel, Haken 1976: Appel, Kenneth - Haken, Wolfgang, Every planar map is four colorable, "Bulletin of the American Mathematical Society", 82, 1976, pp. 711-712.

Birman 1991: Birman, Joan S., Recent developments in braid and link theory, "Mathematical intelligencer", 13, 1991, pp. 52-60.

Browder 1976: Browder, Felix E., Problems of present day mathematics, in: Mathematical developments arising from Hilbert problems, "Proceedings of symposia in pure mathematics", 28, 1976, pp. 35-79.

Crapo, Rota 1970: Crapo, Henry - Rota, Gian Carlo, On the foundations of combinatorial theory: combinatorial geo-metries, Cambridge (Mass.), Mathematical Institute of Technology Press, 1970.

Dieudonné 1982: Dieudonné, Jean, A panorama of pure mathematics: as seen by N. Bourbaki, New York, Academic Press, 1982 (1. ed.: Panorama des mathématiques pures: le choix bourbachique, Paris, Gauthier-Villars, 1977).

Gödel 1931: Gödel, Kurt, Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme,"Monatshefte für Mathematik und Physik", 38, 1931, pp. 173-198.

Gowers 1999: Gowers, William Timothy, The two cultures of mathematics, in: Mathematics: frontiers and perspectives, edited by Vladimir I. Arnold e altri, Providence (R.I.), American Mathematical Society, 1999, pp. 65-78.

Graham 1995: Handbook of combinatorics, edited by Ronald L. Graham, Martin Grötschel, László Lovász, Amsterdam-Oxford, Elsevier, 1995.

Grossman 1997: Grossman, Jerrold W., Paul Erdös: the master of collaboration, in: The mathematics of Paul Erdös, edited by Ronald L. Graham, Jeroslav Nesetril, Berlin, Springer, 1997, pp. 467-475.

Hoffman 1998: Hoffman, Paul, The man who loved only numbers, New York, Hyperion, 1998.

Hollingdale 1989: Hollingdale, Stuart, Makers of mathematics, London, Penguin, 1989.

James 1981: James, Gordon D., The representation theory of the symmetric group, Reading (Mass.), Addison-Wesley, 1981.

Lam 1991: Lam, Clement W.H., The search for a finite pro-jective plane of order 10, "American mathematical monthly", 98, 1991, pp. 305-318.

Morgenstern, Neumann 1944: Neumann, John von - Morgenstern, Oskar, Theory of games and economic behavior, Princeton, Princeton University Press, 1944.

Paris, Harrington 1977: Paris, Jeff - Harrington, Leo, A natural incompleteness in Peano arithmetic, in: Handbook of mathematical logic, edited by Jon Barwise, Amsterdam, North-Holland, 1977, pp. 1133-1142.

Ray-Chaudhuri,Wilson 1971: Ray-Chaudhuri, Dijen K. - Wilson, R.M., Solution of Kirkman's schoolgirl problem, "Proceedings of symposia in pure mathematics", 19, 1971, pp. 187-203.

Robertson, Seymour 1983: Robertson, Neil - Seymour, Paul D., Graph minors, I: Excluding a forest, "Journal of combinatorial theory (B)", 35, 1983, pp. 39-61.

Schechter 1998: Schechter, Bruce, My brain is open: the mathematical journeys of Paul Erdös, New York, Simon & Schuster, 1998.

Shor 1998: Shor, Peter W., Quantum computing, in: Proceedings of the international congress of mathematicians, Berlin 1998, "Documenta Mathematica" Extra Volume ICM 1998, I, pp. 476-486 (disponibile in http://www.mathematik.uni-bielefeld.de/DMV-J/xvol-icm/00/Shor.MAN.dvi).

Swart 1980: Swart, Edward R., The philosophical implications of the four-color problem, "American mathematical mon-thly", 87, 1980, pp. 697-707.

Tutte 1998: Tutte, William T., Graph theory as I have known it, Oxford, Clarendon, 1998.

Tymoczko 1980: Tymoczko,Thomas, Computers, proofs and mathematicians: a philosophical investigation of the four-color proof, "Mathematics magazine", 53, 1980, pp. 131-138.

Welsh 1993: Welsh, Dominic J.A., Complexity: knots, colourings and counting, Cambridge, Cambridge University Press, 1993.

Wilson 2002: Wilson, Robin J., Four colours suffice: how the map problem was solved, London, Allen Lane, 2002.