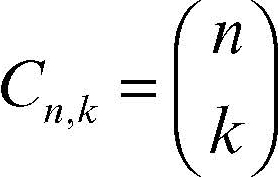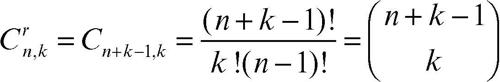combinazione

combinazione

combinazione o combinazione semplice di n elementi di classe k, ognuno dei raggruppamenti distinti formati da k elementi estratti da un insieme S di n elementi (essendo k intero non negativo e k ≤ n). Per indicare i diversi gruppi che si possono formare con gli n elementi prendendone ogni volta k si utilizza talvolta l’espressione equivalente «combinazione di n elementi a k a k». Valgono le seguenti proprietà:

• ciascun raggruppamento contiene k elementi;

• uno stesso elemento non può presentarsi più volte in uno stesso raggruppamento;

• l’ordine degli elementi non ha importanza;

• si intendono distinti due raggruppamenti quando differiscono almeno per un elemento.

Per esempio, se in un gioco di carte si ricevono 4 carte da un mazzo di 40, la mano che si riceve è una delle possibili combinazioni di 40 elementi di classe 4. Una combinazione di n elementi di classe k è quindi un sottoinsieme formato da esattamente k elementi di un insieme finito S di cardinalità n e rappresenta ognuna delle possibili scelte non ordinate di k elementi tra n.

Il numero di tutte le combinazioni di n elementi di classe k è indicato con il simbolo C_n,k. Se k = 0 la particolare combinazione altro non è che l’insieme vuoto, per cui C_n,0 = 1; in generale vale la seguente formula:

nella quale il punto esclamativo indica il fattoriale del numero. L’espressione precedente, utilizzando il simbolo del coefficiente binomiale, può essere scritta in quest’altro modo:

che si legge «n sopra k». Va osservato che, poiché scegliere k elementi tra n equivale a non scegliere i rimanenti n − k, per ogni k ≤ n si ha C_n,k = C_n,n−k.

Qualora sia possibile ripetere ogni elemento, fino a k volte, si parla di combinazione con ripetizione. Il numero delle combinazioni con ripetizione di n elementi di classe k è dato dalla formula seguente: