compattificazione
compattificazione
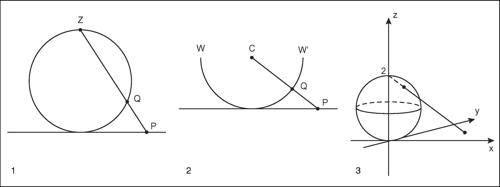
compattificazione procedimento mediante il quale a partire da uno spazio topologico X si costruisce una sua estensione compatta. Se X è localmente compatto, il procedimento si riduce all’aggiunta di un solo punto (compattificazione di Aleksandrov, dal nome del matematico russo P.S. Aleksandrov). Per esempio, la retta reale può essere compattificata con l’aggiunta di un solo punto: ∞, cioè il punto all’infinito. Per rappresentare questo procedimento si proietti un generico punto P della retta su una circonferenza tangente alla retta, il centro di proiezione Z essendo il punto diametralmente opposto al punto di tangenza. L’immagine di R è la circonferenza privata del punto Z; pertanto essa non è compatta. L’aggiunta di Z rende compatta la circonferenza; Z corrisponde idealmente al punto all’infinito di R. La metrica di R non può essere preservata, la topologia sulla circonferenza essendo data dalla distanza cordale, cioè d(Q, Q′) è la lunghezza della corda QQ′. Alternativamente, proiettando dal centro C, si può rendere compatta la retta reale con l’aggiunta dei due punti −∞ e +∞, ottenendo la cosiddetta retta estesa [−∞, +∞], gli intorni di tali punti essendo definiti rispettivamente dalle semirette {x < a} e {x > b}. Tale retta corrisponde a una semicirconferenza e i punti −∞ e +∞ ai suoi estremi W e W′.
Il piano complesso C si estende in modo analogo, attraverso un’opportuna corrispondenza, a una sfera, la cosiddetta sfera di Neumann. Infatti, nello spazio cartesiano tridimensionale (x, y, z) si identifica il piano complesso con il piano (x, y, 0) e si considera la sfera di raggio 1 e centro C(0, 0, 1). La sfera ha equazione x 2 + y 2 + (z − 1)2 = 1; il generico punto P(x0, y0, 0) del piano xy è posto in corrispondenza con un punto della sfera, considerando l’intersezione tra la sfera e la retta che congiunge P con il punto (0, 0, 2). Al punto (0, 0, 2) è associata nella corrispondenza la retta all’infinito del piano xy. Come per la metrica, anche le strutture algebriche di R e C non sono compatibili con questo ampliamento.