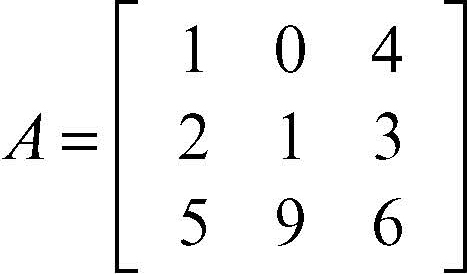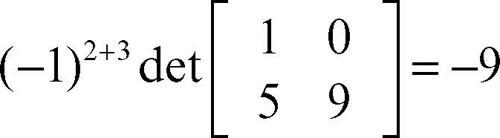complemento algebrico

Enciclopedia della Matematica (2013)

complemento algebrico


complemento algebrico o cofattore, dell’elemento aij di una matrice quadrata A di ordine n è il determinante della sottomatrice di ordine n − 1 ottenuta sopprimendo in A la riga i-esima e la colonna j-esima, preso con il suo segno oppure con il segno opposto a seconda che il numero i + j sia pari oppure dispari. Per esempio, se

formula

allora il complemento algebrico dell’elemento di posto (2, 3), che è 3, è

formula

La somma dei prodotti degli elementi di una riga (o colonna) di A per i rispettivi complementi algebrici è uguale al determinante di A; la somma dei prodotti degli elementi di una riga (o colonna) per i complementi algebrici di un’altra riga (o colonna) è uguale a zero.

Vedi anche
minore Diritto Secondo l’ordinamento italiano, in base all’art. 2 c.c. (come sostituito dall’art. 1, l. 39/1975), il soggetto che è ancora in età minore, che cioè non ha ancora compiuto il diciottesimo anno di età. Matematica M., o determinante m., di una matrice è il determinante costituito dagli elementi ... sommatoria Simbolo operatorio che permette di indicare in modo conciso la somma di più addendi muniti di indice; il simbolo di s. è un sigma maiuscolo (Ʃ) accompagnato da un indice variabile in un certo intervallo o in un certo insieme: per es., ∑4i=1 xi (che si legge: somma di xi per i che va da 1 a 4) è uguale ... eleménto invèrso In algebra, considerato un insieme A, si dice e.i. di un elemento a appartenente ad A, rispetto a una data operazione binaria (∙) definita in A con elemento neutro e, un elemento a´ tale che siano verificate le relazioni a∙a´=a´∙a=e. In un gruppo, ogni elemento ammette uno e un solo elemento inverso. ... algebra Uno dei rami fondamentali delle scienze matematiche: in senso lato l’a. studia le operazioni, definite in un insieme, che godono di proprietà analoghe a quelle delle ordinarie operazioni dell’aritmetica. Con significato specifico è sinonimo di sistema ipercomplesso. La parola al-giabr è usata per la ...
Tag
Altri risultati per complemento algebrico
  • cofattore
    Enciclopedia on line
    Biologia In biochimica, qualsiasi sostanza a basso peso molecolare necessaria all’attività enzimatica. Sono c. i coenzimi, le vitamine non ancora classificate come coenzimi e gli attivatori di varia natura, tra cui vari metalli. matematica C. di un elemento di una matrice Il determinante della matrice ...
Vocabolario
algèbrico
algebrico algèbrico agg. [der. di algebra] (pl. m. -ci). – Di algebra, che concerne l’algebra: calcoli a., somma a., analisi a., ecc.; in partic.: espressione a., ogni scrittura in cui compaiano numeri, lettere e indeterminate, queste ultime...
compleménto
complemento compleménto s. m. [dal lat. complementum, der. di complere «compiere»]. – 1. Ciò che completa una cosa: l’educazione familiare è c. necessario di quella impartita a scuola; esercizî pratici a c. delle nozioni teoriche. 2. In...