complessita computazionale
complessita computazionale
complessità computazionale o complessità di calcolo, teoria che, nell’ambito della teoria della computazione, analizza le risorse (quali il tempo e la memoria) necessarie per effettuare un determinato calcolo, sulla base di parametri indipendenti dallo specifico elaboratore che lo eseguirà. Si definisce complessità computazionale l’operatore che fornisce il numero di operazioni necessarie a risolvere un determinato problema in funzione del numero di dati da trattare, usando l’algoritmo più efficiente possibile. In base al grado di complessità, si classificano i problemi e si individuano le migliori strategie finalizzate alla ricerca delle soluzioni. Le funzioni computabili sono suddivise in varie classi di complessità computazionale: dato un problema di decisione (un problema cioè la cui soluzione può essere solo «sì» o «no»), si dice classe di complessità P l’insieme dei problemi risolubili in un tempo polinomiale (correlato alla dimensione del problema), classe di complessità NP l’insieme dei problemi verificabili in un tempo polinomiale (→ problemi P e NP). Non esiste oggi una dimostrazione rigorosa dell’equivalenza fra le classi di complessità P e NP: il problema è di estrema rilevanza, tanto da essere stato incluso nel 2000 fra i → problemi del millennio, i sette più importanti problemi matematici irrisolti.
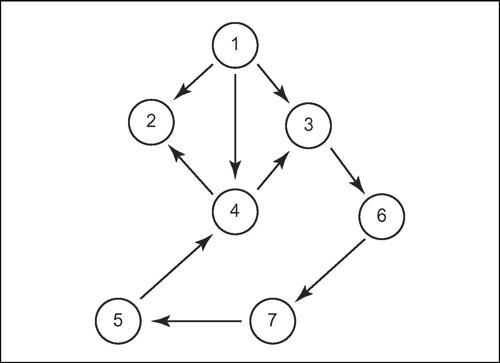
Un problema viene descritto ordinariamente mediante alcuni parametri di cui non sono specificati tutti i valori. Per esempio, dato un grafo orientato G(X, A) con X insieme dei nodi e A insieme degli archi, la determinazione di un cammino dal nodo u al nodo v rappresenta un problema in cui i parametri sono rappresentati dal grafo G e dai vertici u e v. La specificazione di particolari valori assunti dai parametri è definita in genere istanza del problema. Una particolare istanza del problema dato è la seguente: dato il grafo orientato G in figura, si determini un cammino che, a partire dal vertice 1, termini al vertice 7; per esempio, la successione 1, 4, 3, 6, 7 è una possibile soluzione in funzione della particolare istanza del problema.
Spesso un problema P è posto in forma di ottimizzazione (più brevemente O): la ricerca del numero minimo di archi che compongono un cammino tra nodi specifici di un grafo (anche detto problema SP, dall’inglese shortest-path) può essere espressa nel seguente modo: dati un grafo G(X, A, p) orientato e pesato con pesi p non negativi sugli archi, due nodi u e v, quanto vale la lunghezza l del cammino minimo che unisce i nodi u e v? Un’altra modalità di richiesta è il problema posto in forma di riconoscimento o di decisione (più brevemente R): si dice che un problema P è espresso nella forma di riconoscimento R, se la risposta a P può essere solo «sì» o «no». La forma di riconoscimento dell’esempio precedente è: dato un grafo G(X, A, p) orientato e pesato sugli archi con pesi p non negativi, due nodi u e v, un numero k ∈ N, esiste un cammino di lunghezza l ≤ k?
Quando un’istanza di un problema di riconoscimento ammette una risposta affermativa, l’istanza stessa è detta affermativa, mentre è negativa in caso contrario. Le due forme di richiesta applicate a uno stesso problema sono equivalenti, ossia ciascuna implica l’altra: O ⇔ R. Infatti, considerando i casi separatamente, si ha:
• O ⇒ R: sempre riferendosi all’esempio precedente, se si conosce il valore k̄ della lunghezza del minimo cammino, si può rispondere al problema posto in forma di riconoscimento: se k̄ ≤ k la risposta sarà affermativa, altrimenti sarà negativa;
• R ⇒ O: risulta verificata anche l’implicazione inversa; infatti se si considera inizialmente il valore massimo M nell’insieme delle soluzioni in cui si trova la soluzione ottima (valore massimo che nell’esempio corrisponde alla somma di tutti i pesi p presenti nel grafo G) si risolve il problema in forma di riconoscimento imponendo il valore di k uguale a M/2. Se la risposta è «sì», ciò implica che il cammino minimo ha lunghezza non superiore a M/2, pertanto si può iterare il procedimento risolvendo il problema di riconoscimento con k = M/4. Se la risposta è «no», invece, si impone al passo successivo k = 3M/4. Questa procedura è detta ricerca dicotomica, in quanto si basa sulla scelta del semintervallo in cui sicuramente ricade la soluzione del problema, dopo aver dimezzato l’insieme delle possibili soluzioni e operato una scelta tra le due opzioni. Dopo al più un numero di passi pari a log2M si ottiene il valore ottimo k̄ richiesto.
Pertanto, se si ha a disposizione una procedura per la soluzione di un problema in forma di riconoscimento è possibile, attraverso un algoritmo di ricerca dicotomica, giungere alla soluzione del problema posto in forma di ottimizzazione. Inoltre, si può dimostrare che se il problema di riconoscimento è risolto in modo efficiente, si giunge alla soluzione del problema di ottimizzazione con la medesima efficienza.
Un aspetto dei problemi, in qualsiasi forma essi vengano definiti, è tuttavia quello della loro difficoltà intrinseca di risoluzione. Come già anticipato, un problema appartiene alla classe di complessità computazionale P se per esso esiste un algoritmo di soluzione di complessità polinomiale, ossia se il tempo di risoluzione è una funzione polinomiale delle dimensioni dei valori in input; questo accade se l’algoritmo risolutivo ha una complessità di calcolo dell’ordine O(nα), con α > 0 (→ O grande). L’appartenenza di un problema alla classe P può essere sinonimo di facilità di risoluzione solo se l’esponente α ha un valore sufficientemente basso da consentire l’identificazione del problema polinomiale con un problema facile. Per esempio, un algoritmo dotato di complessità O(n13) è polinomiale, ma prevede un costo in termini di tempo di calcolo non trascurabile. Anche se questa non è una regola generale, una volta trovato un algoritmo polinomiale per la risoluzione di un problema, è possibile individuare, attraverso una metodologia di riduzione della complessità, un algoritmo equivalente dotato però di complessità inferiore rispetto all’originario.
Spesso non è noto se esista o meno un algoritmo di soluzione polinomiale, ma si può essere a conoscenza di un’informazione aggiuntiva K, chiamata certificato, che permette di verificare in tempo polinomiale se i dati del problema hanno la proprietà desiderata. Ciò vuol dire che esiste un algoritmo di verifica, dipendente da K e dai dati del problema, che controlla in tempo polinomiale l’esistenza di una soluzione del problema avente le proprietà richieste. Non si conosce, per esempio, nel caso generale se il problema della ricerca di un ciclo hamiltoniano su un grafo sia risolubile in tempo polinomiale; se tuttavia si è in possesso di un certificato K che specifichi l’ordine dei vertici incontrati nel cammino, si può verificare in tempo polinomiale l’esistenza del ciclo controllando gli spigoli tra i vertici consecutivi dichiarati da K. Se il ciclo hamiltoniano ha n archi, il controllo richiederà un tempo dell’ordine di O(n), quindi polinomiale. Si definisce, quindi, la classe di complessità computazionale NP come la classe dei problemi che, posti in una qualsiasi forma di riconoscimento o di decisione, sono verificabili in tempo polinomiale. Non si decide in tempo polinomiale se l’istanza è affermativa o meno, ma si verifica il problema in tempo polinomiale, data un’istanza affermativa del problema. L’appartenenza a NP è quindi meno riduttiva dell’appartenenza a P. Infatti, affinché un problema sia in NP non è necessario che sia risolubile in tempo polinomiale, ma solo che, se l’istanza è affermativa, esso sia verificabile in tempo polinomiale. Al contrario, se un problema è polinomiale allora appartiene sicuramente a NP. Infatti, considerando un’istanza affermativa di un problema P, è sufficiente usare l’algoritmo polinomiale di risoluzione, che richiede una complessità polinomiale, verificando che alla fine produca la risposta «sì»; quindi P ⊆ NP.
La classe NP riveste un’importanza notevole in quanto la maggior parte dei problemi di riconoscimento o decisione appartiene a essa. La richiesta che, una volta calcolata la soluzione di un problema, essa sia rispondente alle proprietà del problema attraverso una verifica polinomiale appare senza dubbio molto ragionevole e risponde alle necessità di ricerca mediante calcoli più semplici possibili. Occorre infine precisare che non tutti i problemi esistenti appartengono a NP: esistono altre classi di problemi, il cui significato e interesse è tuttavia meramente teorico e di scarso interesse pratico.