complessita della rete
complessita della rete
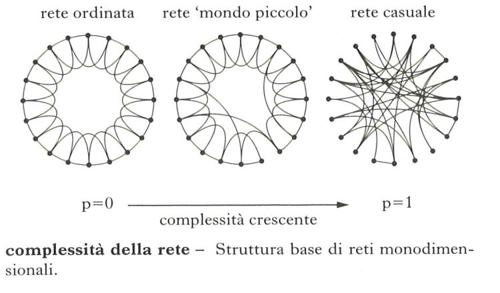
complessità della réte. – Grado di articolazione della struttura di una rete, sia essa rete biologica o sociale, naturale o artificiale. Tale struttura determina il comportamento della rete in risposta agli stimoli – sia interni sia esterni – e ne configura quindi una sua complessità. Si osservano diverse strutture variamente complesse, che si formano in base al processo di crescita della rete e alle logiche che lo determinano. Per es., in informatica, il fatto che i nuovi siti web per rendersi visibili si aggancino di preferenza ai siti più frequentati, come Facebook o Google, porta fisiologicamente, senza alcuna regia preordinata, alla formazione di una rete configurata in maniera complessa, con pochi siti ricchissimi di link e moltissimi siti con pochi link. Una tale rete assume particolari capacità in termini di resistenza agli attacchi, velocità di trasferimento delle informazioni, vulnerabilità ai virus, sviluppo e adattamento. Nell’accezione di network o web, la rete è sia strumento di organizzazione sia architettura dei sistemi complessi adattativi. Nel caso delle telecomunicazioni, e in particolare del web, il presupposto semantico del termine si può far risalire a Norbert Wiener (1950), il padre della cibernetica, per cui esiste un’ampia rete di comunicazioni che connette persone a persone, persone a macchine, macchine a persone e macchine a macchine. Componenti di una rete sono i nodi e le connessioni tra nodi (link). Una rete può essere mono, bi- o multidimensionale; la rete internet che si estende fisicamente (seppure a macchia di leopardo) sulla superficie della Terra si può assimilare a una rete bidimensionale. Lo studio delle reti fa parte della cosiddetta matematica discreta e si basa sulla teoria dei grafi, che mette in evidenza il fatto che piccoli cambiamenti nella struttura della rete possono far emergere o inibire specifiche caratteristiche di percorribilità. Gli sviluppi attuali degli studi delle reti hanno avuto avvio alla fine degli anni Cinquanta del 20° secolo, quando i matematici Paul Erdös e Alfréd Rényi descrissero una rete topologicamente complessa con un grafo random. È seguita poi una fitta serie di nuove definizioni, approfondimenti e tassonomie delle reti grazie agli studi negli anni Settanta dello psicologo Stanley Milgram e del sociologo Mark Granovetter (legami forti, legami deboli e ponti sociali in una rete); e ancora, negli anni Novanta, dei matematici Duncan Watts e Steve Strogatz e dei fisici Réka Albert e Albert-Lázló Barabási (reti scale free, o a invarianza di scala, descritte da una legge di potenza). Grazie a un tale moltiplicarsi delle ricerche, si è oggi in grado di individuare la struttura di una qualsiasi rete e di prevederne di conseguenza il comportamento di massima rispetto a caratteristiche come la velocità di trasferimento delle informazioni o la resistenza agli attacchi, con applicazioni specifiche nell’ambito delle reti informatiche e delle comunità che su tali reti crescono, collaborano ed entrano in conflitto.Gli indicatori fondamentali che si possono utilizzare per valutare le caratteristiche strutturali di una rete sono due: la lunghezza caratteristica (L), che rappresenta la media dei percorsi minimi che servono per passare da un qualsiasi nodo della rete a qualsiasi altro; il coefficiente di aggregazione, o di clustering (k), che quantifica l’idea di vicinato, misurando in media quanti dei vicini di un nodo sono a loro volta vicini tra di loro. Oltre a questi due principali parametri indicatori, ce ne sono molti altri che aiutano a evidenziare le proprietà delle reti che dipendono dalla loro articolazione. Utilizzando questi strumenti si sono costruiti modelli matematici sofisticati di reti a una o più dimensioni, definendo così alcune macrocategorie. In maniera sintetica – per l’aspetto strettamente tecnologico delle reti, come la costruzione ad anello, a stella o secondo altre configurazioni – le due categorie più semplici, quelle estreme, ideali, non presenti in natura, sono rappresentate in fig.: le reti regolari o ordinate (k e L entrambi elevati) e le reti casuali o random (k e L entrambi bassi). Nella stessa fig., al centro, è rappresentato il modello intermedio (diffuso in natura e nelle reti artificiali), che si ottiene staccando e riconnettendo a caso alcuni legami in una rete regolare: si costruisce in questo modo una struttura molto più efficace nella trasmissione dei segnali. Tale tipologia di reti è caratterizzata infatti da un coefficiente k elevato (con un vicinato ricco) e una lunghezza L bassa (due nodi anche lontani sono collegabili tra loro con pochi link, hanno cioè pochi gradi di separazione). Le reti sociali di questo tipo (e in particolare quelle catalizzate dal web) che meglio si sanno adattare ai cambiamenti sono organizzate in gruppi molto coesi (cluster) con legami forti tra i componenti del gruppo e connessioni sparse o ponti sociali (legami deboli) tra un gruppo e l’altro: la presenza di tali ponti sociali permette di diminuire i gradi di separazione e quindi di far acquisire alla rete una maggiore efficacia nella diffusione dei segnali. I punti critici di una rete sono generalmente esaminati attraverso l'applicazione di specifici modelli matematici e simulazioni, che consentono di valutarne la risposta secondo una serie di requisiti. Se ne ricavano indicazioni condizionali: per es., se la rete favorisce la diffusione di segnali positivi (per es. notizie) o negativi (virus); se gode di buona, modesta o cattiva velocità nel collegare punti distanti; se corre il rischio o meno di essere distrutta da attacchi casuali o da attacchi mirati; se riesce a crescere adattandosi con pericolo lieve o elevato di collasso; se ha capacità di resilienza, di autoaggiustamento dopo un attacco esterno; se ha capacità di generare velocemente o lentamente, con fluidità o rigidità, nuove tendenze, nuovi fenomeni o nuove configurazioni autoorganizzandosi dal basso, senza leader, nella logica bottom-up.