Computer. Hardware

Computer. Hardware

Obiettivo dei sistemi informatici è la soluzione automatica di problemi computazionali. Un problema computazionale è un insieme di domande (dati, ingressi) per ciascuna delle quali ci sono una o più risposte (risultati, uscite) corrette. A partire dalla domanda, si vuole produrre una risposta corretta. Per esempio, in aritmetica, nel problema della fattorizzazione, la domanda codifica (immaginiamo in base 10) un numero intero positivo, mentre la risposta codifica una lista di numeri primi il cui prodotto eguaglia il numero fornito nella domanda.

L’automatismo della soluzione si esplica su due livelli. A livello logico, un algoritmo definisce in maniera univoca e specificabile in termini finiti un processo di passi elementari che permettono di trasformare la domanda in una risposta corretta per il problema in questione. A livello fisico, una macchina esegue i passi previsti dall’algoritmo elaborando una rappresentazione materiale dell’informazione contenuta nella domanda fino a produrre una rappresentazione materiale della risposta.

Dato un problema, si può costruire una macchina dedicata esclusivamente alla sua soluzione; in questo caso, la struttura fisica della macchina codifica l’algoritmo scelto. Va però annoverata tra le pietre miliari della storia del pensiero la scoperta – fatta negli anni Trenta del secolo scorso dal matematico britannico Alan Turing – dell’esistenza di calcolatori universali, in grado cioè di gestire un qualsiasi problema computazionale che ammetta una soluzione algoritmica. L’estrema versatilità della macchina calcolatrice universale è alla base del successo e della diffusione dei calcolatori nella società odierna.

Nella macchina universale di Turing, l’informazione – sia quella relativa all’algoritmo da eseguire, sia quella relativa ai dati di ingresso – è codificata in forma digitale, ovvero mediante parole composte con un numero finito di simboli, tipicamente due (0 e 1), detti bit (contrazione di binary digit). Oggi esistono standard per la codifica mediante sequenze di bit dei più disparati tipi di informazione: quantità matematiche, testi, immagini, segnali audio, segnali video, algoritmi. Una volta che l’informazione da trattare è stata trascritta in forma binaria, un passo elementare del processo di calcolo diviene una ben precisa regola per ottenere da una certa sequenza di 0 e 1 un’altra sequenza di 0 e 1. Tecnicamente, una tale regola è nota come funzione booleana.

Qualsiasi funzione booleana si può realizzare componendo un’unica funzione opportunamente scelta, per esempio la funzione NAND. Essa elabora due bit per produrne un terzo, cui assegna il valore 0 se entrambi i bit dati valgono 1 e il valore 1 in tutti gli altri casi. Disponendo di un dispositivo fisico in grado di calcolare la funzione NAND e di uno di memoria – in grado cioè di conservare il valore di un bit nel tempo – si può realizzare qualsiasi sistema digitale, incluso il calcolatore universale.

Il dispositivo fisico utilizzato per la realizzazione del NAND o di altre operazioni booleane equivalenti è oggi quasi esclusivamente il transistore al silicio, che nel corso degli anni, è stato reso sempre più piccolo, veloce ed energeticamentc efficiente. L’attuale tecnologia integrata permette di fabbricare chip di 4÷8 cm², contenenti centinaia di milioni di transistori che commutano (cioè passano da 0 a 1 o viceversa) in decine di picosecondi.

Il calcolatore con memoria ad accesso random

Un calcolatore universale è una macchina che, a partire da un algoritmo e da un insieme di dati, produce i risultati dell’esecuzione di quell’algoritmo sui dati stessi. Se ne possono concepire varie tipologie, da un punto di vista sia logico sia fisico.

A livello logico (comunemente indicato con il termine architettura) un calcolatore è definito dal linguaggio, detto linguaggio macchina, nel quale vanno formulati gli algoritmi affinché essi siano eseguibili direttamente dal calcolatore stesso. Un algoritmo formulato in un linguaggio specifico viene solitamente chiamato programma. Un linguaggio ha una dimensione sintattica, che definisce quali sequenze di caratteri siano valide come programmi, e una dimensione semantica, che definisce cosa costituisca una corretta esecuzione di un programma.

A livello fisico, un calcolatore è definito da una disposizione spaziale e un’interconnessione di dispositivi elementari (quali transistori e collegamenti elettrici) in grado di immagazzinare, trasmettere e modificare bit di informazione. La struttura di un calcolatore risulta spesso più comprensibile se definita in termini di moduli che svolgono funzioni di una certa complessità (quale un moltiplicatore di numeri). A questo livello di astrazione, si parla di organizzazione del calcolatore.

Quasi tutte le realizzazioni architetturali proposte in pratica – in particolare nei prodotti commerciali – si possono considerare varianti di un unico modello, noto come macchina con memoria ad accesso random (RAM, Random access machine) o macchina di von Neumann (da John von Neumann che, in un famoso rapporto del 1945, la descrisse per la prima volta). A livello architetturale, il modello RAM è sopravvissuto essenzialmente invariato a oltre mezzo secolo di eccezionali evoluzioni tecnologiche, mentre a livello organizzativo l’evoluzione è stata continua e profonda. Nel resto di questo paragrafo approfondiremo l’architettura RAM, presentandone una realizzazione basata su un’organizzazione molto semplice.

Architettura

Nel modello RAM si assume l’esistenza di una struttura logica, la memoria, che consiste in una sequenza infinita di celle in corrispondenza biunivoca con i numeri naturali (0,1,2,...). Il numero che corrisponde a una cella è detto indirizzo. Ciascuna cella è in grado di immagazzinare una parola, cioè una stringa di bit di qualsiasi lunghezza finita, che costituisce il contenuto della cella. Tale contenuto può essere inserito tramite operazioni di scrittura (che fanno perdere traccia del contenuto precedente) e preso in visione con operazioni di lettura (che vedono quanto inserito dalla più recente scrittura). Lettura o scrittura possono riferirsi a un indirizzo qualsiasi. La RAM è un modello ideale, prevedendo un numero infinito di celle e un numero infinito di configurazioni possibili per singola cella. Nella pratica entrambi i numeri sono finiti, ancorché essi siano cresciuti rapidamente per oltre mezzo secolo: la memoria di un tipico calcolatore per uso personale di questi ultimi anni ha centinaia di milioni di celle, ognuna contenente tipicamente 32 o 64 bit.

Un programma è una sequenza finita di istruzioni identificate dal loro numero d’ordine e ognuna di esse è un elemento di un repertorio (instruction set). Per ogni istruzione del repertorio, si definiscono il formato della stringa di bit (codice binario) che la rappresenta e il significato operativo, cioè le azioni che ne costituiscono l’esecuzione. Nell’ambito del modello RAM la differenziazione delle architetture avviene nella definizione del repertorio: durante mezzo secolo di evoluzione dei calcolatori ne sono stati usati vari tipi, contenenti da poche decine a centinaia di istruzioni.

Discuteremo in quanto segue solo le tipologie base di istruzione, al fine di illustrare i principî generali. Vi sono istruzioni di elaborazione, che permettono di ottenere nuovi valori applicando opportune operazioni a valori già disponibili; istruzioni di controllo, che determinano l’ordine in cui le istruzioni vanno eseguite; istruzioni di ingresso/uscita, che permettono di comunicare con il mondo esterno. Le istruzioni di elaborazione operano su dati presenti nella memoria e producono un risultato che verrà a sua volta scritto su di essa. L’istruzione dovrà quindi specificare: (a) i dati da elaborare (gli operandi); (b) il tipo di operazione da eseguire (per es., addizione o moltiplicazione); (c) la posizione di memoria in cui scrivere il risultato dell’operazione.

Decine di tipi di operazione sono contemplati nel repertorio dei calcolatori odierni e una rassegna va oltre i nostri scopi. Vale la pena invece soffermarsi brevemente sui tre metodi tipicamente previsti per specificare un dato. Il modo immediato consiste nello specificare il valore dell’operando direttamente nell’istruzione, quello diretto nello specificare nell’istruzione l’indirizzo di memoria al quale leggere o scrivere il valore dell’operando e infine quello indiretto nello specificare nell’istruzione l’indirizzo al quale leggere o scrivere il valore dell’operando. Il modo indiretto può apparire inultimente complicato ma gioca un ruolo fondamentale a livello di principio, svincolando la quantità di memoria che l’esecuzione di un programma può utilizzare dal numero di istruzioni che compongono il programma stesso. Infatti, un programma può accedere a una cella in modo diretto solo se un’istruzione contiene letteralmente l’indirizzo z di quella cella; per un accesso indiretto è al contrario sufficiente che un’operazione eseguita dal programma calcoli il valore z e lo scriva in una cella direttamente indirizzabile dal programma stesso. Altrettanto importante è il fatto che la stessa istruzione possa essere eseguita più volte operando su dati diversi, aggiornando il contenuto delle celle di memoria alle quali l’istruzione legge l’indirizzo dei dati stessi.

Passiamo ora al controllo. Ricordiamo che un programma consiste di una sequenza di istruzioni che resta fissa durante l’esecuzione. Un’esigenza primaria è quella di poter eseguire ripetutamente un gruppo di istruzioni, tipicamente su dati diversi, in modo da specificare con un programma conciso un calcolo che richiede una grande quantità di elaborazioni; altrettanto importante è la possibilità di prevedere azioni diverse in funzione dei dati da elaborare. Le necessità sopra esposte sono soddisfatte con l’introduzione di istruzioni di salto condizionato: il formato specifica un dato, poi una condizione che può valere o meno per quel dato e infine una posizione nel programma. Sia I un’istruzione di salto. Se all’atto dell’esecuzione essa non vale per il dato si passa a eseguire l’istruzione che, nel programma, appare subito dopo I. Altrimenti (cioè se la condizione è vera), si salta a eseguire l’istruzione nella posizione del programma specificata da I. Al repertorio di controllo va aggiunta l’istruzione di arresto (halt), che pone fine all’esecuzione del programma. Infine, rendiamo esplicita la regola che dopo l’esecuzione di un’istruzione di elaborazione si passa all’istruzione ad essa immediatamente successiva nel programma. Convenendo che quando un programma viene lanciato è inizialmente eseguita la prima istruzione nella sequenza statica, le regole sopra citate assieme al valore dei dati in memoria determinano in modo univoco l’istruzione da eseguire successivamente, dando così luogo a una sequenza dinamica che termina con l’esecuzione di halt (situazione generalmente desiderabile) o prosegue indefinitamente (situazione generalmente indesiderabile, che tipicamente porta a un arresto forzato dall’esterno del programma).

Come già accennato, un calcolatore è in generale collegato con altri sistemi con i quali può scambiare informazione. Nella pratica, questi sistemi sono di varia natura: tastiere, terminali, stampanti, modem, memorie a disco, reti di telecomunicazioni, apparecchiature audio e video, strumenti di misura, sensori, e – sempre più frequentemente – altri calcolatori. Possiamo schematizzare concettualmente la situazione assumendo l’esistenza di un unico canale di comunicazione tra il calcolatore e i vari organi di ingresso e uscita, ciascuno dei quali è identificato da un indirizzo. Il repertorio contiene un’istruzione di ingresso, che identifica una cella di memoria nella quale scrivere la parola in arrivo dal canale, nonché l’indirizzo d’ingresso da cui si intende ricevere. Una simmetrica istruzione di uscita identifica una cella di memoria il cui contenuto va inviato sul canale, nonché l’indirizzo del destinatario.

Organizzazione elementare

fig. 3

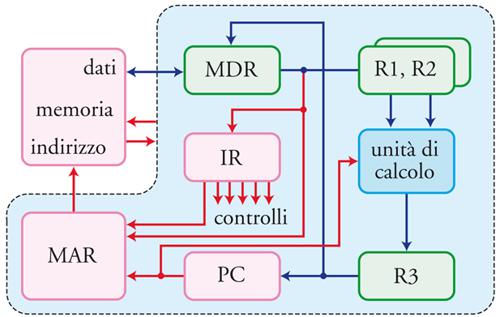
Definita l’architettura della RAM, presentiamo adesso una sua organizzazione minimale (fig. 3), trascurando per semplicità gli organi di ingresso e uscita. Questa organizzazione prevede tre componenti fondamentali: l’unità di controllo, l’unità di memoria e l’unità di calcolo o funzionale. L’unità di controllo è dotata di alcuni dispositivi, i registri, in grado di immagazzinare parole al pari delle celle di memoria. L’unità di controllo può copiare il contenuto da un registro a un altro. Le interazioni con la memoria avvengono attraverso i registri MAR (Memory address register) e MDR (Memory data register). In risposta a un comando di lettura, la memoria copia nell’MDR il contenuto della cella il cui indirizzo si trova nel MAR. A un comando di scrittura, la memoria risponde copiando il contenuto dell’MDR nella cella indirizzata dal MAR. Tre registri (R1, R2 e R3), sono dedicati alle interazioni con l’unità di calcolo, alla quale l’unità di controllo può inviare la richiesta di effettuare una data operazione sui dati contenuti nei registri R1 ed R2 e di scrivere il risultato nel registro R3.

L’organizzazione che stiamo descrivendo prevede che il programma da eseguire sia inizialmente caricato in celle consecutive di memoria, a partire da un indirizzo prestabilito. Per semplicità assumiamo che il codice di ciascuna istruzione del repertorio occupi esattamente una parola. Un registro particolare dell’unità di controllo, detto contatore di programma e denotato PC (Program counter), mantiene l’indirizzo della cella che contiene l’istruzione da eseguire. Un altro registro denotato IR (Instruction register) contiene l’istruzione in via di esecuzione.

Un programma viene iniziato caricando l’indirizzo della sua prima istruzione nel PC. L’unità di controllo gestisce quindi il processo di esecuzione, presiedendo al funzionamento coordinato di tutti i componenti coinvolti. A titolo di esempio, si consideri un’istruzione che richiede di eseguire un’addizione; i due addendi e il risultato sono specificati in modo diretto dagli indirizzi a b, e c. L’esecuzione di tale istruzione comporta le seguenti fasi:

1) L’unità di controllo ottiene dalla memoria l’istruzione da eseguire. Più in dettaglio, copia il PC nel MAR, invia alla memoria un comando di lettura e, a lettura avvenuta, copia il contenuto dell’MDR nell’IR; infine incrementa di 1 il valore del PC (in preparazione per la successiva istruzione).

2) L’unità di controllo decodifica l’istruzione e inizia a inviare i comandi alle altre unità per portare a buon fine l’esecuzione.

3) L’unità di controllo chiede alla memoria i dati, estraendo i loro indirizzi a e b dall’istruzione, e li deposita temporaneamente nei registri R1 ed R2.

4) L’unità di controllo invia il comando di somma all’unità di calcolo, la quale lo esegue e deposita il risultato in R3.

5) Il contenuto di R3 viene scritto in memoria: l’unità di controllo copia R3 in MDR, estrae l’indirizzo c dall’IR, lo copia nel MAR e invia un comando di scrittura alla memoria. L’esecuzione dell’istruzione è completata: si può passare all’istruzione successiva.

Istruzioni diverse da quella considerata comportano semplici varianti della sequenza sopra descritta. In particolare nel caso di salto condizionato, quando la condizione è verificata, il PC viene aggiornato al valore indicato nell’istruzione stessa.

L’organizzazione in passi dell’esecuzione di un programma implica una cadenza temporale nel funzionamento del sistema scandita da un segnale periodico, chiamato clock. Durante ciascun passo, l’applicazione di appropriati operatori booleani all’insieme di bit che caratterizzano lo stato attuale del processore produce un nuovo insieme di bit che caratterizzano il nuovo stato. Le prestazioni del processore aumentano al diminuire del periodo di clock, che tuttavia deve essere abbastanza lungo da permettere la valutazione della più complessa operazione booleana associata alla transizione. Uno dei fondamentali problemi ingegneristici legati all’evoluzione del processore è quindi quello di incrementare la frequenza del clock, mantenendo la corretta funzionalità del sistema.

Contesto evolutivo

L’organizzazione dei calcolatori si è evoluta ricercando prestazioni sempre più elevate e sostenendo per oltre quarant’anni un tasso di crescita impressionante, probabilmente superiore a quello di qualunque altro prodotto dell’ingegno umano. L’aspetto più importante delle prestazioni di un calcolatore è il tempo di esecuzione dei programmi, che tuttavia non è facilmente riassumibile in un’unica quantità. Con tutte le cautele del caso, è comunque ragionevole stimare che negli ultimi trent’anni le prestazioni siano raddoppiate mediamente ogni 18 mesi, crescendo complessivamente di un fattore di circa un milione. Questa crescita esponenziale viene detta legge di Moore, generalizzando la previsione formulata nel 1965 da Gordon E. Moore che il numero di dispositivi in un singolo circuito integrato sarebbe raddoppiato ogni due anni.

L’evoluzione dei calcolatori ha beneficiato sia dell’aumento della velocità dei dispositivi elettronici elementari sia dell’aumento del numero di dispositivi che possono essere utilizzati in un sistema. Giova quindi inquadrare il percorso evolutivo di processori e sistemi di memoria in termini delle tendenze tecnologiche e dei vincoli applicativi che ne hanno storicamente definito il contesto. I primi calcolatori elettronici, a partire dagli anni Quaranta, sono stati realizzati con dispositivi elementari singoli (valvole e successivamente transistori) connessi tra di loro tramite circuiti stampati e cavi. A partire dalla metà degli anni Sessanta la tecnologia del circuito integrato ha permesso di incorporare un grande numero di dispositivi su un unico substrato di semiconduttore (quasi sempre silicio), tanto che sotto la guida di Federico Faggin nel 1971 venne prodotto dalla società statunitense Intel il primo processore completamente realizzato in un solo chip (chiamato, con un termine poi rimasto nell’uso, microprocessore). L’industria ha perseguito con determinazione lo sviluppo di processori single-chip che, al momento, costituiscono la totalità delle realizzazioni esistenti.

La tecnologia dei circuiti integrati ha registrato progressi in varie direzioni. L’elemento chiave è stato la riduzione della cosiddetta feature size, che indicheremo con il simbolo λ. Si tratta della minima dimensione lineare sagomabile dal processo fotolitografico con cui vengono realizzati i circuiti, ridotta di circa 200 volte dai 10 μm del 1971 agli 0,045 μm del 2007. Come conseguenza, è diminuito il tempo di commutazione dei transitori, in prima approssimazione proporzionale a λ se si mantiene costante il campo elettrico o a λ² se si mantiene costante la tensione di alimentazione. Questa legge di scala ha inizialmente implicato notevoli progressi, ma è stata resa irrilevante dal fatto che il tempo dominante è diventato quello associato alla propagazione del segnale da un punto all’altro di uno stesso circuito integrato. Da alcuni anni ormai il cosiddetto FO4 (il tempo necessario per eseguire una commutazione e trasportare il segnale ottenuto ad altri 4 transistori di uguali dimensioni) si è quasi stabilizzato su valori dell’ordine di 0,02÷0,04 ns.

La diminuzione del tempo di commutazione dei dispositivi si traduce in una crescita della frequenza di clock; si è passati dal megahertz (periodo dell’ordine dei 1000 ns) nei primi anni Settanta a qualche gigahertz (periodo dell’ordine di frazioni di 1 ns) nei primi anni Duemila. Il periodo del clock ha registrato un decremento superiore rispetto al tempo di commutazione dei dispositivi, principalmente grazie all’adozione della tecnica del pipelining, che decompone l’elaborazione in compiti più semplici e eseguibili da circuiti che richiedono una sequenza più breve di commutazioni di transistori.

fig. 4

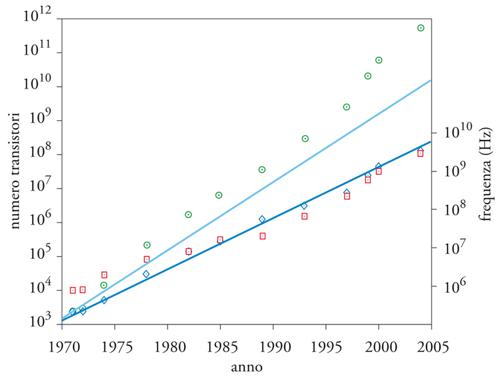
La diminuzione di λ porta anche a una crescita del numero di transistori realizzabili per unità di area, inversamente proporzionale a λ²; infatti, l’area minima per realizzare un transistore è di qualche decina di λ². A questo aumento di densità si è accompagnato un aumento di un fattore di circa 20 dell’area A dei chip realizzabili in maniera affidabile: dal 1971 al 2007 è passata da alcuni decimi a quasi una decina di centimetri quadri. Complessivamente la quantità A/λ², un indicatore della capacità del chip di ospitare transistori, è cresciuta di circa 500.000 volte. Questo incremento è stato ampiamente ma non totalmente sfruttato: il primo microprocessore (nel 1971) conteneva 2250 transitori mentre una versione del processore Pentium 4 realizzata nel 2004 ne contiene 125 milioni, quasi 60.000 volte di più. Nel complesso, durante l’intero trentennio in considerazione la previsione formulata da Moore è stata ben rispettata, come illustrato dal grafico nella fig. 4, che riporta il numero di transistori della famiglia di processori sviluppati dalla Intel.

Riassumendo, nel periodo considerato (1971-2005) si è registrato un fattore di crescita F_c≃3×10³ per la frequenza di clock e F_t≃10⁵ per il numero di transistori per chip (si veda ancora la fig. 4). Il secondo fattore è alquanto maggiore del primo ma nessuno dei due, da solo, può dar conto dell’aumento di circa 10⁷ verificatosi per le prestazioni dei processori: la sinergia tra essi è stata fondamentale. Si può anche constatare come il numero totale di commutazioni di dispositivo per unità di tempo, una misura del potenziale elaborativo di un chip, sia cresciuto di un fattore F_c×F_t≃3×10⁸ e cioè circa 30 volte di più della crescita in prestazioni. Per mettere in prospettiva questa discrepanza, osserviamo che mentre l’aumento di velocità dei dispositivi si traduce quasi direttamente in un aumento di velocità dell’intero sistema, risulta più arduo da sfruttare pienamente quello del numero di dispositivi disponibili. La ragione principale è che, nonostante la loro presenza permetta di eseguire contemporaneamente varie operazioni, il modello RAM è basato su una definizione seriale, passo per passo, della computazione. Ciò limita la quantità di operazioni che per la loro indipendenza logica possono essere eseguite contemporaneamente, numero che caratterizza il parallelismo dell’elaborazione. Aggirare questo ostacolo ha richiesto soluzioni innovative e spesso ingegnose nell’organizzazione del calcolatore, soluzioni della cui efficacia si comincia da alcuni anni a vederne i limiti. Un fatto che spinge inesorabilmente nella direzione di paradigmi di calcolo di tipo parallelo.

Evoluzione del processore

Nel mezzo secolo circa che ci separa dalle prime realizzazioni le prestazioni dei calcolatori elettronici sono dunque cresciute di molti ordini di grandezza. Durante questa evoluzione, l’architettura è rimasta quella della macchina con memoria ad accesso random, con varianti che hanno riguardato essenzialmente il repertorio di istruzioni. Dopo alcuni decenni durante i quali è cresciuto sia il numero di istruzioni presenti nel repertorio che la complessità delle operazioni da esse svolte, a partire dai primi anni Ottanta è prevalsa una tendenza opposta: dalle architetture dette CISC (Complex instruction set computer) si è passati a quelle dette RISC (Reduced instruction set computer) oggi predominanti nel mercato dei microprocessori.

Le architetture RISC introducono la nozione di registro (per esempio R1, R2 ed R3 descritti sopra) a livello architetturale, per cui le istruzioni possono far riferimento direttamente a un certo numero di registri, separando chiaramente lo scambio dati tra memoria e unità di controllo (operato da istruzioni che copiano il contenuto di una cella di memoria in un registro o viceversa) dalla elaborazione dei dati (operata da istruzioni che coinvolgono solo registri). Questa separazione necessita di un maggior numero di istruzioni per eseguire un fissato algoritmo, ma permette di semplificare sia il formato delle istruzioni sia l’unità di controllo. Inoltre, se un dato viene utilizzato ripetutamente da istruzioni successive, si possono risparmiare un certo numero di scritture e letture in memoria. Nel seguito, faremo riferimento a questa tipologia di architettura.

Più radicali sono stati gli sviluppi riguardanti l’organizzazione dei calcolatori, divenuta via via più complessa per sfruttare la crescita del numero di dispositivi utilizzabili. Una prima linea di evoluzione è la crescita della dimensione di parola, inizialmente di 4 o 8 bit e attualmente giunta a 64 bit. Poiché 8 bit sono insufficienti per contenere i dati tipici nella maggior parte di algoritmi di interesse scientifico o gestionale, oppure per identificare un indirizzo di memoria, il dato deve essere spezzato in più segmenti assegnati ad altrettanti registri e manipolato in sequenza. La crescita della dimensione di parola elimina questa necessità, producendo un aumento di prestazioni immediatamente apprezzabile dall’utilizzatore. Tale crescita però perde utilità quando la dimensione eccede le esigenze di rappresentazione dei dati della maggior parte delle applicazioni.

Una seconda linea di evoluzione affine punta a realizzare le unità funzionali e altri moduli del processore basandosi su algoritmi in grado di trattare contemporaneamente un maggior numero di bit all’interno di una parola. Ciò ridiede un maggior numero di porte logiche, ma permette di completare le operazioni più rapidamente. Per esempio, consideriamo un’addizione tra due dati, espressi in formato binario con n bit. È possibile elaborare in sequenza i due bit di stesso peso degli addendi calcolando il risultato pertinente al bit considerato e il riporto, da considerare nel calcolo del bit successivo: un circuito con un piccolo numero di porte logiche, utilizzato n volte per trattare tutti i bit, produce il risultato in tempo proporzionale a n. Algoritmi più sofisticati, realizzabili da circuiti con un numero di porte logiche proporzionale a n, elaborano simultaneamente tutti i bit degli operandi e calcolano il risultato con un’unica applicazione del circuito.

Una terza, fondamentale linea di evoluzione è legata all’idea di sovrapporre temporalmente l’esecuzione di più istruzioni successive, tecnica nota universalmente come pipeline. Come abbiamo visto, l’esecuzione di un’istruzione comporta varie attività che conviene raggruppare nelle seguenti fasi, identificate da una sigla:

1) IF (Instruction fetch), lettura dell’istruzione da eseguire e calcolo dell’indirizzo della prossima istruzione;

2) ID (Instruction decode), decodifica dell’istruzio-ne letta;

3) OP (Operands), lettura degli operandi;

4) EX (Execute), manipolazione degli operandi e calcolo del risultato;

5) WR (Write back), scrittura del risultato in un re-gistro.

fig. 5

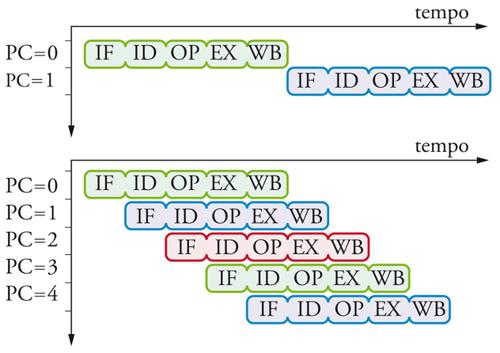
La tecnica di pipeline consiste nell’organizzare l’hardware in tanti stadi quante sono le fasi richieste dall’elaborazione (cinque, nel nostro esempio), permettendo così a istruzioni diverse di essere elaborate contemporaneanmente in stadi diversi come illustrato in fig. 5. Pur non riducendo il tempo di esecuzione T della singola istruzione, la tecnica permette di completare una nuova istruzione in sequenza nel tempo richiesto da un singolo stadio, detto periodo della pipeline. In prima approssimazione, il periodo vale T/5 se i vari stadi richiedono circa lo stesso tempo.

L’analisi precedente si basa su assunzioni che conviene esplicitare: (a) stadi diversi impiegano risorse diverse; (b) i vari stadi richiedono lo stesso tempo per istruzione; (c) l’esecuzione di una istruzione può procedere indipendentemente da quella delle altre. Vari ostacoli rendono difficile soddisfare queste ipotesi in un processore e raggiungere le prestazioni che esse implicano. Prenderemo adesso in esame questi ostacoli e le soluzioni organizzative che hanno permesso di superarli in gran parte, rendendo le tecniche di pipeline un elemento chiave per incrementare le prestazioni dei calcolatori.

La pipeline valorizza le risorse utilizzate in una sola fase, come i circuiti di decodifica operanti esclusivamente durante la fase ID, senza la quale resterebbero inattive la maggior parte del tempo. Alcune risorse possono però essere richieste in fasi diverse: per esempio, la stessa unità di calcolo potrebbe calcolare sia l’indirizzo della prossima istruzione sia il risultato di un’addizione. Analogamente, la memoria e la sua interfaccia sono utilizzate sia durante la lettura dell’istruzione sia durante l’esecuzione della istruzione stessa se questa è un trasferimento di dati con la memoria. La soluzione a questo problema è la duplicazione della risorsa in tutte le fasi di pipeline in cui è richiesta, soluzione resa sempre più praticabile dalla crescita della quantità di dispositivi disponibili.

Un problema più serio si presenta quando un’istruzione ha bisogno di accedere ai risultati di un’altra istruzione che logicamente la precede nel programma ma che, a causa dell’organizzazione della pipeline, non sono ancora disponibili. Consideriamo per esempio la seguente sequenza di istruzioni:

0: add R4, R5 ? R6

1: add R6, R5 ? R7

2: sub R4, R5 ? R8

3: add R4, R4 ? R9.

Nella pipeline a 5 stadi discussa in precedenza, l’istruzione 1, all’inizio della sua fase OP, legge da RG un operando ivi scritto dall’istruzione 0 alla fine della sua fase WB. Un’osservazione attenta della fig. 5 (parte inferiore) rivela che la lettura dovrebbe aver luogo due periodi prima della scrittura. Per garantire una corretta esecuzione, va fermato il flusso di istruzioni che entrano nella pipeline nonché l’avanzamento dell’istruzione 1 e di quelle successive già sotto esecuzione (2 e 3) per due periodi, fino a che R6 non è stato aggiornato. L’esecuzione viene così allungata di due periodi; nel caso limite in cui questa situazione si ripetesse per ogni coppia di istruzioni successive il tempo di esecuzione risulterebbe triplicato. Si osservi adesso che le istruzioni 2 e 3 non utilizzano il risultato dell’istruzione 1, per cui riordinando le istruzioni nella sequenza 0,2,3,1 non si altera la semantica del programma e si evita di dover fermare il flusso attraverso la pipeline. Questo riordinamento può essere talvolta operato dal compilatore e tuttavia molti processori moderni lo effettuano direttamente in hardware. Le istruzioni vengono inizialmente sistemate in una struttura dati interna al processore e se ne abilita l’esecuzione quando tutti gli operandi sono disponibili, anche se qualche istruzione precedente non è ancora pronta. Si parla in questo caso di esecuzione del programma in disordine (out-of-order). I relativi circuiti di controllo sono estremamente complessi (costituendo in alcuni casi il 30% di tutta la logica del processore) e di delicata messa a punto. D’altra parte, questa tecnica permette di riutilizzare in maniera efficiente programmi già compilati per processori diversi ma con lo stesso repertorio di istruzioni, o di programmi di cui non è neppure più disponibile la sorgente compilabile.

Una generalizzazione di questo approccio porta al processore superscalare, concepito come un insieme di risorse hardware (operatori di calcolo aritmetico, registri contenenti dati, registri di accesso alla memoria ecc.) a disposizione per l’esecuzione delle istruzioni. Le istruzioni entrano in una coda di attesa e vengono inviate in esecuzione quanto un modulo dell’unità di controllo, detto stazione di prenotazione (reservation station), determina la disponibilità di tutti gli operandi e di tutte le risorse hardware necessarie, incluso il registro in cui va scritto il risultato. A seconda di tale disponibilità, nessuna, una o più istruzioni possono entrare in esecuzione a ogni nuovo ciclo di clock.

Un’altra interdipendenza tra istruzioni si presenta in occasione dell’esecuzione di salti condizionati. In questo caso, l’indirizzo della prossima istruzione da eseguire diventa disponibile solo al completamento dell’istruzione corrente. Soluzioni più sofisticate dell’ovvio blocco della pipeline si basano sulla possibilità di predire, in modo statistico, il valore della condizione e iniziare a eseguire ulteriori istruzioni di conseguenza. Naturalmente, deve essere possibile annullare gli effetti delle operazioni iniziate in tal modo, qualora la predizione si riveli sbagliata. Questo può essere particolarmente difficile nel caso di salti condizionati multipli. Alcuni metodi di previsione, detti statici, si basano esclusivamente sulla struttura del programma e pertanto sono messi in atto a livello di compilazione. Per esempio, in corrispondenza del costrutto linguistico detto loop (ciclo che prevede N esecuzioni di un gruppo di istruzioni) la condizione di fine loop è verificata solo una volta su N; per questa ragione si predice che risulti falsa e la previsione è confermata con alta probabilità. Tuttavia, oggi si ricorre prevalentemente a predittori di salti dinamici, basati sulla raccolta – operata da circuiti specializzati – di informazione sul comportamento della singola istruzione di salto durante le sue esecuzioni più recenti. Per esempio, si può prevedere che il comportamento della prossima esecuzione ripeta quello della volta precedente. Tecniche leggermente più sofisticate di questa raggiungono un’alta affidabilità statistica, predicendo correttamente oltre il 95% dei salti per molti programmi d’interesse. L’hardware necessario è piuttosto complesso, dovendo mantenere dati statistici relativi a migliaia di istruzioni nonché consultare e aggiornare tali dati in una frazione del ciclo del processore. Tenendo presente che, secondo il dato sperimentale – mediamente e in un programma tipico – è presente un salto ogni 5÷6 istruzioni, con probabilità di predizione corretta al di sopra del 95% per il singolo salto, è possibile prevedere correttamente le istruzioni da eseguire per varie decine o anche alcune centinaia di passi della macchina.

fig. 6

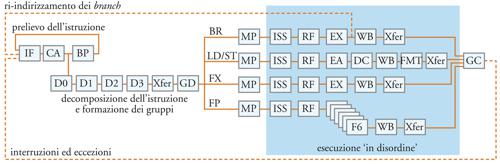
Si può desumere dalla discussione del presente paragrafo che la complessità di un moderno processore è enormemente superiore a quella del semplice modello che abbiamo descritto in apertura a scopo esemplificativo. A titolo di esempio, la fig. 6 mostra la struttura delle pipeline utilizzate dal processore POWER4, realizzato dall’IBM nel 2001. In questa realizzazione, un unico chip contiene due processori, le rispettive cache di primo livello, una cache comune di secondo livello (la memoria cache è discussa più avanti) e una serie di dispositivi ausiliari.

Evoluzione del sistema di memoria

Anche l’organizzazione della memoria dei calcolatori si è evoluta significativamente, sia per motivi tecnologici, sia per rendere il sistema informatico nel suo complesso più facilmente accessibile agli utenti. Il contesto tecnologico è stato caratterizzato dal fatto che la velocità dei processori è cresciuta in modo sensibilmente più rapido della velocità delle memorie, che oggi sono due ordini di grandezza più lente. Se non si ponessero rimedi a questa discrepanza, il processore sarebbe quasi sempre inattivo, in attesa di ricevere dalla memoria i dati da elaborare. Sono stati in effetti adottati vari rimedi che risultano efficaci nella misura in cui i programmi presentino alcune regolarità nel modo in cui fanno uso dei dati.

Un primo tipo di regolarità, chiamato localizzazione temporale, si presenta quando la stessa cella di memoria viene utilizzata da un programma ripetutamente in un breve periodo. La localizzazione temporale può essere sfruttata introducendo nel sistema una memoria notevolmente più piccola ma anche più veloce della memoria principale, detta memoria cache, nella quale si mantiene una copia delle celle della memoria principale recentemente utilizzate. La gestione della cache è effettuata da hardware specializzato all’interno del sistema di memoria. La scelta delle celle di cui tenere una copia in cache è cruciale per le prestazioni e richiede delicati compromessi tra vantaggi di velocità e complessità della realizzazione hardware. Un secondo tipo di regolarità, chiamato localizzazione spaziale, si presenta quando celle di memoria vicine tra loro (in termini di indirizzo) vengono utilizzate in un breve periodo, durante l’esecuzione del programma. Per sfruttare questa proprietà, la memoria viene concettualmente suddivisa in linee, ciacuna delle quali contiene un dato numero di celle consecutive. Quando una cella è richiesta dal processore, viene portata in cache tutta la linea a cui essa appartiene, rendendo così più rapido l’accesso alle altre celle della stessa linea. Un terzo tipo di regolarità si presenta specialmente in programmi per calcoli scientifici e di ingegneria: gli indirizzi generati contengono delle progressioni aritmetiche che un apposito modulo hardware riesce a individuare. Si possono così precaricare nella cache i dati in modo che siano già disponibili quando richiesti dal processore, tecnica nota come prefetching.

Le memorie cache sono state introdotte verso la metà degli anni Sessanta. Al crescere del divario di velocità tra memoria e processore, si è introdotto un secondo e poi un terzo livello di cache. Questa serie di livelli di dimensioni e tempi di accesso crescenti viene detta gerarchia di memoria. Un’altra direzione in cui si migliorano le prestazioni consiste nel rendere il sistema di memoria capace di accettare nuove richieste da parte del processore prima di avere completato la gestione delle richieste precedenti, utilizzando meccanismi simili a quello della pipeline discusso a proposito del processore.

Per completare, sia pure a grandi linee, la descrizione del sistema di memoria, resta da trattare la memoria a dischi. Fisicamente un disco contiene alcune superfici circolari dette facce, ciascuna suddivisa in centinaia di migliaia di anelli detti tracce; ogni traccia è in grado di immagazzinare vari milioni di bit, codificati dalla direzione del campo magnetico. La capacità complessiva del disco si avvicina quindi a 10¹² bit (1 terabit), superiore di circa due ordini di grandezza rispetto alla memoria principale e con costi minori. Quando risiedono in posizioni contigue sulla stessa traccia, i trasferimenti di dati tra disco e memoria principale possono raggiungere svariati gigabit al secondo. Quando invece essi sono in posizioni arbitrarie, il trasferimento diventa migliaia di volte più lento. Si intuisce quindi come tali trasferimenti vadano programmati in maniera parsimoniosa e strutturata, sfruttando attentamente la localizzazione temporale e spaziale.

La memoria a dischi svolge funzioni diverse. Da un lato, fornisce un supporto per la memorizzazione permanente di dati e programmi utilizzati in tempi diversi o da utenti distinti. Tipicamente questi dati sono strutturati in file, a loro volta organizzati in un file system. Una seconda funzione, oggi centrale per molti sistemi, viene svolta dai dischi in relazione al meccanismo di memoria virtuale. Gli obiettivi perseguiti sono molteplici: (a) eseguire programmi che utilizzano più spazio di quanto sia disponibile nella memoria principale; (b) permettere a programmi diversi di condividere, alternandosi, l’uso del processore; (c) permettere a programmi diversi di condividere dati o porzioni di programma, mantenendone in memoria una sola copia. Tutti questi obiettivi possono essere raggiunti se i dati di interesse per i vari programmi possono essere allocati con flessibilità in memoria principale, nonché spostati temporaneamente su disco quando si esaurisce lo spazio disponibile nella memoria stessa. Gestire questa flessibilità pone sfide notevoli cui i moderni sistemi fanno fronte con sofisticati moduli hardware e complesse procedure software. Queste fanno parte del sistema operativo, un programma che ha il controllo dell’intero calcolatore e sotto la cui supervisione vengono eseguiti tutti gli altri programmi.

Concludendo, possiamo osservare quanto l’organizzazione di un attuale sistema di memoria sia più complessa della semplice collezione di celle direttamente indirizzabili del modello RAM. È certamente un notevole successo della scienza e dell’ingegneria dei calcolatori l’aver creato un ponte efficace tra un modello semplice, che favorisce lo sviluppo del software, e una realtà implementativa assai più complessa, che si rende necessaria per tradurre in prestazioni l’enorme potenziale reso disponibile dalla tecnologia.

Chip multiprocessori

La riduzione dei tempi mediante l’esecuzione contemporanea di più istruzioni trova i suoi limiti nel fatto che le istruzioni dipendono l’una dall’altra. Questo ostacolo si può superare attraverso un paradigma radicalmente innovativo per il progetto e la programmazione degli algoritmi, detto calcolo parallelo.

Un programma parallelo viene eseguito simultaneamente da processori diversi su dati diversi. Le varie copie del programma contemporaneamente in esecuzione devono poter comunicare tra di loro, per cooperare alla soluzione dello stesso problema. Le comunicazioni possono avvenire sia attraverso zone di memoria condivisa (paradigma shared memory), dove il mittente scrive e il destinatario legge, o attraverso un esplicito sistema di scambio di messaggi (paradigma message passing). Come si può intuire, il progetto di un algoritmo parallelo e la sua codifica in un programma possono rappresentare notevoli sfide. Per ottenere buone prestazioni, è cruciale che il problema da risolvere sia suddiviso in tanti sottoproblemi risolubili contemporaneamente e in maniera il più possibile autonoma, in quanto le comunicazioni tra processori necessitano dello scambio di segnali che possono richiedere tempi significativi rispetto a quelli delle operazioni.

A partire dagli anni Sessanta il calcolo parallelo è stato oggetto di studi e ricerche via via crescenti. Verso la metà degli anni Ottanta, i calcolatori paralleli hanno iniziato a essere commercialmente disponibili e successivamente hanno subito una rapida evoluzione. Nel novembre del 2007, il supercomputer più potente era la macchina IBM BlueGene/L con 212.992 processori, capace di circa mezzo milione di miliardi di operazioni al secondo. Nonostante questi prodigiosi sviluppi, fino a qualche anno fa l’uso dei calcolatori paralleli è rimasto relativamente limitato, soprattutto a causa del grado di sofisticazione che si richiede per lo sviluppo di software parallelo. Negli ultimi anni però la situazione sta mutando drasticamente. Infatti, mentre continua a crescere il numero di dispositivi disponibili su un singolo chip, si è ormai a corto di espedienti che consentano di utilizzare tali dispositivi per velocizzare il processore tradizionale. Le case costruttrici di microprocessori hanno quindi cominciato a organizzare i nuovi chip come macchine parallele, oggi tipicamente con 4÷8 processori, un numero destinato a crescere di uno o due ordini di grandezza nei prossimi decenni. Il calcolo parallelo sta pertanto uscendo dalla nicchia, sia pure significativa e prestigiosa, nella quale è cresciuto e si avvia rapidamente a rappresentare la norma. Questa evoluzione non è priva di difficoltà, soprattutto sul versante del software. Sia il mondo accademico sia quello industriale sono alla ricerca di strade che rendano la programmazione parallela più accessibile per facilitarne l’uso su grande scala, ma non si profila all’orizzonte alcuna panacea.

Oltre alla ovvia difficoltà di prevedere molteplici attività concorrenti, le prestazioni di un programma parallelo dipendono in maniera critica dalla riduzione dei trasferimenti di dati, all’interno del processore, tra processore e memoria, o tra diversi processori di un sistema parallelo. È ovvio che in un sistema di calcolo le comunicazioni siano una conseguenza necessaria dello scambio di informazioni tra diverse componenti del sistema. Tuttavia, intuitivamente, l’elaborazione dell’informazione appare più impegnativa del suo trasporto. Durante i primi decenni di evoluzione dell’informatica, questa intuizione è stata in linea con le caratteristiche delle tecnologie all’epoca disponibili e ha condizionato in vari modi lo sviluppo della disciplina. Peraltro, quest’intuizione è destinata a essere ribaltata a mano a mano che il progresso rimuove gli ostacoli accidentali e conduce a tecnologie soggette solo ai limiti fondamentali derivanti dalla natura fisica delle realizzazioni. In estrema sintesi, i vincoli fisici cruciali sono il limite superiore alla velocità dei segnali e il limite inferiore alla quantità di spazio necessaria per immagazzinare o elaborare un bit. Studi nell’ambito della scienza del calcolo dedicati alle conseguenze di tali limiti hanno messo in evidenza come per molti problemi computazionali, al crescere della quantità dei dati da elaborare, il tempo di calcolo sia sempre più dominato dal tempo di trasferimento dei dati da una parte all’altra della macchina e sempre meno dalla elaborazione booleana degli stessi, il cui peso percentuale tende asintoticamente a zero. Queste considerazioni sono sufficienti a fare intravedere come l’ottimizzazione delle comunicazioni, lungi dall’essere una preoccupazione transitoria, continuerà a crescere d’importanza sia nella progettazione delle macchine sia in quella degli algoritmi. In sintesi, le spinte tecnologiche rendono il calcolo parallelo una soluzione inevitabile anche per macchine realizzate su un singolo chip. Ne risultano macchine le cui potenziali prestazioni sono molto elevate, ma possono essere raggiunte solo attraverso uno sforzo significativo nello sviluppo del software. Anche se il percorso dettagliato sarà probabilmente ricco di sorprese, non è difficile prevedere che i prossimi dieci anni saranno caratterizzati da significativi progressi nella scienza e nell’ingegneria del calcolo, con rilevanti ricadute in tutti i domini applicativi.

Bibliografia

Bay, Bilardi 1995: Bay, Paul - Bilardi, Gianfranco, Deterministic on-line routing on area-universal networks, “Journal of the Association for Computing Machinery”, 42, 1995, pp. 614-640.

Bilardi, Preparata 1995: Bilardi, Gianfranco - Preparata, Franco P., Horizons of parallel computation, “Journal on parallel and distributed computing”, 27, 1995, pp. 172-182.

Cormen 2001: Cormen, Thomas H. e altri, Introduction to algorithms, Cambridge (Mass.)-London, MIT Press, 2001.

Culler 1998: Culler, David - Singh, Jaswinder P. - Gupta, Anoop, Parallel computer architecture: a hardware/software approach, San Francisco, Morgan Kaufmann, 1998.

Hennessy, Patterson 1998: Hennessy, John L. - Patterson, David A., Computer organization and design: the hardware/software interface, San Francisco, Morgan Kaufmann, 1998.

Hennessy 2003: Hennessy, John L. - Patterson, David A. - Goldberg, David, Computer architecture: a quantitative approach, Amsterdam-London, Morgan Kaufmann, 2003.

IBM POWER4 System, “IBM journal of research and development”, 46, 2002.

Katz 1994: Katz, Randy A., Contemporary logic design, Redwood City (Cal.), Benjamin-Cummings, 1994.

Moore 1965: Moore, Gordon E., Cramming more components onto integrated circuits, “Electronics”, 38, 1965, pp. 114-117.

Reid 2001: Reid, T.R., The chip: how two Americans invented the microchip and launched a revolution, New York, Random House, 2001.

Tripiccione 1999: Tripiccione, Raffaele, APEmille, “Parallel computing”, 25, 1999, pp. 1297-1316.

Tripiccione 2005: Tripiccione, Raffaele, Strategies for dedicated computing for Lattice Gauge Theories, “Computer physics communications”, 169, 2005, pp. 442-448.

Turing 1926-1937: Turing, Alan, On computable numbers with applications to the Entscheidungsproblem, “Proceedings of the London Mathematical Society (series 2)”, 42, 1936-1937, pp. 230-265; 43, 1937, pp. 544-546.

Von Neumann 1945: von Neumann, John, First draft of a Report on the EDVAC, Contract No. W-670-ORD-492, Philadelphia, University of Pennsylvania, Moore School of Electrical Engineering, 1945 (rist. parziale in: Origins of digital computers: selected papers, edited by Brian Randell, Berlin, Springer, 1982, pp. 383-392).