concavita

concavita

concavità proprietà di una curva piana o di una superficie, strettamente legata a quella di → convessità.

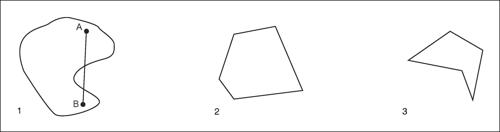
☐ In geometria, una figura piana possiede una concavità quando non è convessa, quando cioè esistono almeno due punti (come A e B in figura) tali che il segmento che li congiunge non appartiene interamente alla figura. Una figura con tale proprietà è detta figura concava. Un angolo è concavo quando contiene i prolungamenti dei lati ed è, quindi, maggiore dell’angolo piatto; un poligono è concavo se almeno uno dei suoi angoli è concavo; nessun triangolo è concavo.

☐ In analisi, caratteristica del grafico di una funzione ƒ(x) di una variabile reale. La funzione si dice volgere la concavità nel verso positivo dell’asse y se in ogni intervallo [a, b] contenuto nel suo dominio il suo grafico sta al di sotto di quello del segmento congiungente i punti (a, ƒ(a)) e (b, ƒ(b)) (funzione convessa). Il grafico della funzione ƒ(x) volge, quindi, la concavità nel verso positivo dell’asse y in un punto x₀ se esiste un intorno di x₀ in cui il grafico di ƒ(x) si trova “al di sopra” della tangente; volge la concavità nel verso negativo dell’asse y se si mantiene “al di sotto” della tangente. Una condizione sufficiente perché il grafico di una funzione due volte derivabile volga nel punto di ascissa x la concavità verso le ordinate positive è che risulti ƒ″(x) > 0, cioè la sua derivata seconda sia maggiore di zero, per ogni x nell’intervallo (a, b). Nel caso di più variabili le definizioni sono analoghe, e la condizione sufficiente è la positività della forma quadratica corrispondente alla matrice hessiana.

Un punto P nel quale una curva cambia di concavità si dice punto di inflessione o di → flesso; in esso la curva è attraversata dalla tangente e, se la curva è il grafico di una funzione derivabile due volte, la derivata seconda della funzione è uguale a 0: ƒ″(x) = 0.