concoide
concoide
concoide o cocloide (cioè a forma di conchiglia), famiglia di curve algebriche piane del quarto ordine. Il caso più semplice è quello in cui la concoide si riferisce a una retta.
Concoide della retta
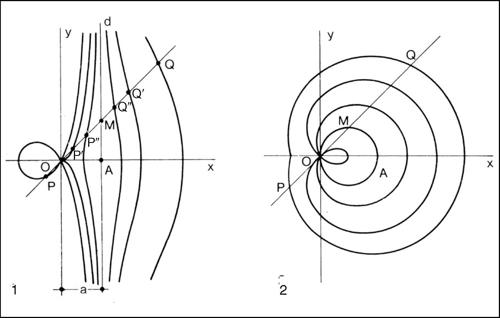
Tale concoide è detta concoide di Nicomede. È generata nel modo seguente: data una retta d (base) e un punto O (polo) esterno alla retta, su ogni trasversale condotta per O e secante d in un punto M si riporti, dall’una e dall’altra parte di M, un segmento MP = MQ avente una lunghezza l assegnata (intervallo); la concoide è il luogo descritto dai punti P e Q al variare della trasversale. Assunta la retta OA, perpendicolare a d e che ne dista a, come asse delle ascisse e O come origine degli assi coordinati ortogonali, l’equazione della concoide della retta è
A seconda del mutuo rapporto esistente tra i parametri a e l la curva presenta in O, rispettivamente, un punto doppio isolato (l < a), una cuspide (l = a) o un nodo (l > a); in tutti i casi, la curva si compone di due rami: ramo esterno, quello descritto dal punto più lontano dal polo O, ramo interno l’altro; la retta d ne è asintoto. Se O è il polo e Ox la retta polare, l’equazione in coordinate polari diventa
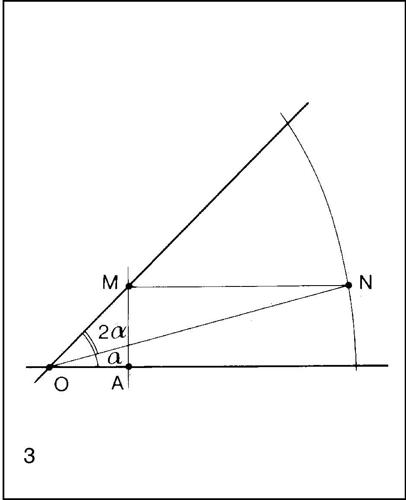
La concoide di Nicomede relativa alla retta è legata al problema della trisezione dell’→ angolo.
Concoide della circonferenza
La definizione di concoide può essere generalizzata, considerando come base, anziché una retta r, una curva qualsiasi. La concoide della circonferenza è generata in modo analogo a quella della retta, ma con base costituita appunto da una circonferenza. La sua equazione è
dove a è la distanza tra O e il centro della circonferenza e l ha lo stesso significato visto in precedenza. Anche la concoide della circonferenza può presentare nell’origine tre diversi punti singolari secondo il mutuo rapporto tra i parametri. In particolare, nel caso l = a la concoide della circonferenza diventa una → cardioide.
Concoide di Sluse
Molto simile alla concoide della retta, trae il suo nome da quello del matematico belga René-François de Sluse (1622-1685). Essa ha equazione:
Considerati nel piano una retta d e un punto O esterno a essa e indicata con a la distanza di O da d, la concoide di Sluse è il luogo dei punti P che si ottengono riportando, nei due sensi, dal punto M di intersezione di d con la retta generica passante per O due segmenti MP e MP′ tali che OM · MP = OM · MP′ = b2 (con b prefissato).