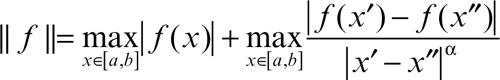Holder, condizione di

Holder, condizione di

Hölder, condizione di (di ordine α, con 0 < α < 1) per una funzione ƒ(x) definita in un intervallo [a, b], indica l’esistenza di una costante H tale che ∀x′, x″ ∈ [a, b] risulta

Una tale funzione si dice hölderiana in [a, b] ed è necessariamente continua, ma non vale il viceversa. Per esempio, ƒ(x) = √x, è hölderiana in [0, 1] di ordine 1/2, mentre

pure essendo continua nel suo insieme di definizione, non soddisfa a una condizione di Hölder di alcun ordine. L’ordine α è anche detto esponente di Hölder. La condizione di Hölder generalizza la condizione di → Lipschitz, che corrisponde al caso α = 1. Lo spazio delle funzioni che soddisfano una condizione di Hölder in [a, b] è uno spazio di Banach con la norma