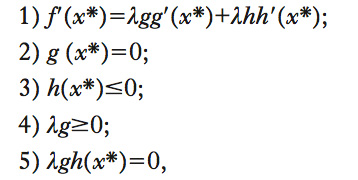Kuhn-Tucker, condizioni di

Kuhn-Tucker, condizioni di

Nei problemi di ottimizzazione vincolata (➔ ottimizzazione p), condizioni necessarie che devono essere verificate in un punto di ottimo. Le condizioni di K.-T. (dal nome dei matematici H.W. Kuhn e A.W. Tucker che le hanno proposte) costituiscono una generalizzazione del metodo dei moltiplicatori di Lagrange (➔ Lagrange, moltiplicatore di; lagrangiano) nel caso in cui siano presenti non solo vincoli di uguaglianza, ma anche di disuguaglianza. Formalmente, si consideri il problema di massimizzazione di una funzione f(x) sotto un vincolo di uguaglianza g(x)=0 e uno di disuguaglianza h(x)≤0, dove x è la variabile di scelta. Le condizioni di K.-T. sono le seguenti:

dove f′, g′ e h′ sono le derivate delle funzioni rispetto a x, e λg e λh sono i moltiplicatori di Lagrange. Le prime 3 condizioni coincidono con quelle del metodo di Lagrange. La 4 e la 5 tengono in considerazione due possibilità: se la condizione h(x)≤0 è stringente nel punto di ottimo, ossia vincola in modo effettivo la determinazione del punto x*, allora essa è verificata con l’uguaglianza, h(x*)=0, e il moltiplicatore di Lagrange λg a essa associato è in genere positivo, perché a uno spostamento del vincolo corrisponde necessariamente una variazione dell’ottimo x*; al contrario, se vale la stretta disuguaglianza h(x*)<0, l’ultima condizione di K.-T. implica che λg=0: poiché il vincolo non è stringente, un suo spostamento marginale non provoca alcuna variazione nella scelta dell’ottimo. Per es., se x è un bene di consumo che entra nella funzione di utilità u(x) di un individuo, allora non può assumere valori negativi, x≥0. Di solito, dato il prezzo del bene, la scelta ottima del consumatore corrisponde a un valore positivo di x. È possibile, tuttavia, che il fruitore non riceva sufficiente utilità dal consumo del bene, rispetto al prezzo, per essere motivato all’acquisto: la scelta ottima è quindi data da x*=0.