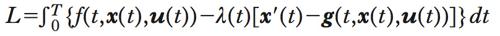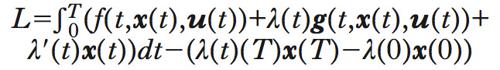trasversalita, condizioni di

trasversalita, condizioni di

trasversalità, condizioni di  Condizioni che si presentano in problemi di ottimizzazione dinamica del tipo a controllo ottimo. In tali problemi si cerca di massimizzare un funzionale F(x)=∫^T₀f(t,x(t),u(t))dt, sotto i vincoli x′(t)=g(t,x(t),u(t)), x(0)=x₀, x(T) uguale a qualche vincolo la cui specificità interviene appunto nelle condizioni di trasversalità.

L’interpretazione del problema in termini dinamici è legata alla visione del parametro t come variabile temporale in un intervallo fra un istante iniziale t=0 e uno terminale t=T (se l’orizzonte è finito). Il vettore u(t) è un vettore di variabili di controllo (cioè che sono liberamente scelte dal decisore per ogni istante di tempo), la scelta delle variabili di controllo determina l’evoluzione del vettore x(t) delle variabili di stato secondo l’equazione di vincolo in cui la derivata x′(t) rispetto al tempo è espressa dalla funzione g. Il funzionale da massimizzare dipende secondo la f sia dalle variabili di stato sia da quelle di controllo (oltrechè eventualmente dal tempo).

La soluzione del problema si richiama alla tecnica dei moltiplicatori di Lagrange utilizzata in problemi di ottimizzazione vincolata statica. A tale scopo, tenendo conto che vi è un vettore di vincoli per ogni istante t, si introduce una funzione moltiplicatore vettoriale λ(t) (detto vettore delle variabili di costato) e si definisce il lagrangiano (➔) del problema come

Utilizzando la tecnica di integrazione per parti, L si può scrivere nella forma alternativa

La componente f(t,x(t),u(t))+λ(t)g(t,x(t),u(t)) dell’integrale è detta hamiltoniano (➔) del problema e si indica con la notazione H(λ,t,x,u). Un fondamentale risultato dovuto a L.S. Pontryagin garantisce che la soluzione ottima u*(t) del problema di controllo si ottenga massimizzando la funzione H(λ,t,x,u)+λ′(t)x(t). La condizione di azzeramento delle derivate rispetto alla terna (u,x,λ) porge le condizioni necessarie ∂H∂(u)=0,−∂H∂(x)=λ′, ∂H∂(λ′)=g=x′. Queste sono analoghe alle condizioni di ottimo del primo ordine per un problema di ottimizzazione statica. A esse si deve (eventualmente) applicare una ulteriore condizione di t., analoga a quelle aggiuntive di Kuhn-Tucker (➔ Kuhn-Tucker, condizioni di), dipendente dal tipo di condizioni al contorno (vincolo terminale) nel modo seguente: se x(T)=x_T è fissato, nessuna condizione (la t. non compare); se x(T)≥x_T, λ(T)≥0 e inoltre λ(T)(x*(T)−x_T)=0; se x(T) libero, λ(T)=0. Per interpretare il ruolo di λ(T), il suo collegamento con le condizioni di ottimo e in particolare con le condizioni di t. si tenga presente che, indicando con V =ʃ^T₀ f(t,x*(t),u*(t))dt il valore della soluzione di ottimo, risulta ∂V∂(x_T)=−∂(T).