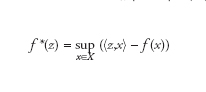coniugata di Fenchel
coniugata di Fenchel
Sia f una funzione convessa definita su uno spazio di Hilbert X; si chiama polare di f, o trasformata o coniugata di Fenchel, o di Legendre, la funzione f * definita da
Poiché, per ogni x fissato, la funzione che compare alla destra dell’equazione precedente è affine (nella variabile z), si ha che f *, supremo di una famiglia di funzioni affini, è una funzione convessa. Si noti che l’operazione di prendere l’estremo superiore può dare come risultato +∞, così che f * sarà, generalmente, a valori estesi. Dalla definizione si ha facilmente che, per ogni x∈X e z∈X′,
〈z, x〉 ≤ f (x) + f *(z).
Per es., la coniugata della funzione f(x)=(1/p)∥x∥π (dove ∥x∥ indica la norma di x) è la funzione f*(z)=(1/p)∥z∥ϑ con (1/p)+(1/q)=1 e la disuguaglianza precedente diventa
〈z, x〉 ≤ (1/p) ∥x∥π + (1/q) ∥z∥ϑ
nota come disuguaglianza di Young.