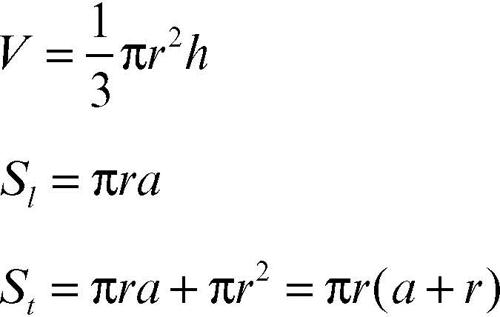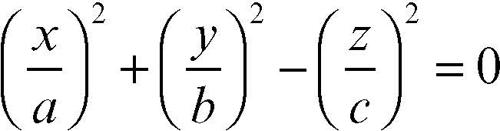cono

cono

cono in geometria elementare e nell’uso comune, con il termine cono, o più propriamente cono finito circolare retto, si intende il solido ottenuto dalla rotazione completa di un triangolo rettangolo attorno a un asse passante per un suo cateto. Esso risulta delimitato da un cerchio detto base e da una superficie curva detta superficie laterale del cono. La superficie laterale e la base costituiscono insieme la superficie totale del cono. Il cateto attorno al quale avviene la rotazione è la sua altezza, l’ipotenusa di tale triangolo rettangolo è l’apotema del cono. L’estremo dell’altezza non appartenente alla base è detto vertice del cono. Indicati, rispettivamente, con h, r, a l’altezza, il raggio della base e l’apotema del cono e indicati, rispettivamente con V, S_l, S_t il volume, l’area della superfìcie laterale e l’area della superficie totale del cono, si hanno le seguenti formule:

Il volume del cono è 1/3 del volume del cilindro circolare retto avente la stessa base e la stessa altezza. Se l’apotema del cono è uguale al diametro della sua base (cioè a = 2r) il cono è detto equilatero; in tal caso la sua sezione con un piano passante per l’asse è un triangolo equilatero.

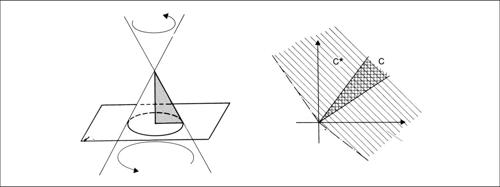
Più in generale, per cono, o più propriamente cono indefinito, si intende la superficie rigata ottenuta assegnando una curva semplice chiusa C, un punto V non appartenente al piano della curva e considerando tutte le rette passanti per V e per i punti di tale curva (direttrice). Con tale definizione il cono assume la forma di “doppio cono”, nel senso ordinario del termine, e quindi ha due falde, cioè due parti distinte che si intersecano nel suo vertice. Sezionando una falda di un cono con un piano generico si ottiene un cono finito, che è retto se tale piano è perpendicolare all’asse. Se la curva C assegnata è una conica, il cono è detto cono quadrico e le sue sezioni con un piano sono le coniche. Se la curva C è un’ellisse o una circonferenza e la retta per V e per il centro della circonferenza o ellisse è perpendicolare al piano della curva C, il cono indefinito è detto, rispettivamente, cono ellittico retto o circolare retto: i rispettivi assi sono le rette passanti per il centro di C e per V.

Un cono indefinito circolare retto può essere anche generato dalla rotazione completa di una retta a, detta generatrice del cono, attorno a una retta h (asse del cono) a essa incidente in V. L’angolo acuto formato dall’asse e dalla generatrice di tale cono è detto apertura del cono. Se la generatrice è perpendicolare all’asse il cono degenera in un piano rigato e di fatto è un piano, pensato come fascio di rette.

L’equazione di un cono indefinito, in un riferimento cartesiano Oxyz in cui l’asse del cono coincide con l’asse z e in cui la curva C è un’ellisse, è:

Se a = b il cono è circolare retto.

Un’ulteriore generalizzazione porta a considerare uno spazio euclideo reale n−dimensionale; in esso un cono avente centro nell’origine è un insieme che, con ogni elemento x, contiene anche tutti gli elementi del tipo tx, per ogni t ≥ 0. Si tratta di un cono a una sola falda detto anche cono puntato. Cono poliedrico convesso è l’intersezione di un numero finito di semispazi originati da iperpiani contenenti l’origine. Cono polare rispetto a un cono convesso K* è l’insieme K* dei punti x dello spazio tali che il prodotto scalare tra x e y non è minore di 0 per ogni y ∈ K*. Se K* è un cono poliedrico, allora il cono polare di K* coincide con K (teorema di Farkas).