Considerazioni metodologiche sullo studio delle funzioni cerebrali
Considerazioni metodologiche sullo studio delle funzioni cerebrali
L'integrazione tra neuroscienze e psicologia è necessaria per comprendere il modo in cui il cervello produce un comportamento intelligente. La psicologia fornisce informazioni sulla natura dell'intelligenza, mentre le neuroscienze servono a comprendere i processi di attivazione nelle strutture neuronali implicate nel comportamento intelligente. Tuttavia, questi due tipi di informazione possono essere integrati solo sulla base di modelli computazionali: in essi, infatti, le caratteristiche delle strutture neuronali vengono messe in relazione ai requisiti computazionali necessari per la produzione del comportamento intelligente. Un importante requisito riguarda l'uso di due tipi differenti di informazioni: quelle utilizzate e immagazzinate in modo permanente e quelle utilizzate solo in modo temporaneo. La produttività del comportamento intelligente dipende dall'interazione tra questi due tipi di informazione. Una volta identificate le strutture nervose preposte, la produzione del comportamento intelligente può essere descritta in termini di interazione tra queste strutture.
Le funzioni cerebrali come computazioni che generano il comportamento
La comprensione del modo in cui il cervello produce un comportamento intelligente è una delle più grandi sfide della scienza moderna. Recentemente ha preso forma un approccio a questo problema, fondato su un insieme interdisciplinare di scienze che vanno sotto il nome di neuroscienze cognitive. L'obiettivo di questo approccio è descritto chiaramente da M.S. Gazzaniga (1995): "A un certo punto, in futuro, la neuroscienza cognitiva sarà capace di descrivere gli algoritmi che guidano gli elementi neuronali strutturali nella attività fisiologica che sfocia nella percezione, nella cognizione, e forse nella coscienza".
Questa citazione suggerisce che, per comprendere le funzioni cerebrali, dobbiamo capire in che modo il comportamento, come la percezione e la cognizione, venga prodotto da algoritmi basati su elementi neuronali. Cioè, dobbiamo "comprendere le funzioni cerebrali in termini di computazioni che danno luogo al comportamento" (Kosslyn e Shin, 1992). Quindi, la comprensione delle funzioni cerebrali richiede l'integrazione della psicologia cognitiva, delle neuroscienze e dell'informatica (o della scienza della computazione). Per questo motivo lo studio delle funzioni cerebrali costituisce uno sviluppo recente nella scienza moderna: ognuna delle tre componenti principali (comportamento, algoritmi ed elementi neuronali) è oggetto di studio di una scienza diversa ed è stato necessario che ciascuna di queste scienze maturasse prima che potesse realizzarsi una loro integrazione.
Per studiare le funzioni cerebrali come computazioni che danno luogo al comportamento, si dovrebbe confrontare la risposta comportamentale di un organismo con i processi di attivazione delle strutture cerebrali che producono quel comportamento. Se queste strutture cerebrali e questi processi di attivazione sono noti, si può costruire un modello che mostri in che modo il cervello produce il comportamento studiato. D'altra parte, una indagine diretta e dettagliata dei processi di attivazione neuronali nel caso del comportamento intelligente è molto difficile, se non impossibile; è invece necessario, a causa della complessità e della varietà coinvolte in questo fenomeno, un approccio più indiretto per studiare il modo in cui il cervello produce un comportamento intelligente. In tale approccio si dovranno integrare gradualmente elementi di informazione sul comportamento, ottenuti dalla psicologia, e sui processi cerebrali, ottenuti dalle neuroscienze, all'interno di modelli che spieghino il comportamento osservato in termini di processi di attivazione neuronale.
Un elemento essenziale di questa integrazione fra risultati di diversa provenienza è l'uso della teoria computazionale. Da un lato, questa teoria fornisce informazioni sulla potenza di calcolo necessaria a un organismo per produrre un certo tipo di comportamento, dall'altro, può essere usata per descrivere le caratteristiche computazionali di particolari processi di attivazione neuronali. In questo modo, si può usare la teoria della computazione come un linguaggio comune con cui mettere in relazione i risultati della neurofisiologia con quelli della psicologia. A questo punto, si possono usare i risultati comportamentali per generare previsioni sul tipo di processi di attivazione neuronale necessari per produrre quel comportamento. Oppure si possono usare le conoscenze sui processi di attivazione neuronale per comprendere il comportamento prodotto da questi processi.
In questo saggio, mi concentrerò in primo luogo sull'uso della teoria computazionale nella integrazione tra neuroscienze e psicologia cognitiva.
Il comportamento come interazione con l'ambiente
Si può formulare un'analisi iniziale delle funzioni cerebrali in termini delle operazioni minime necessarie per la sopravvivenza di un organismo. Per sopravvivere, un animale deve soprattutto procurarsi del cibo ed evitare i predatori. È chiaro che queste due operazioni basilari sono in gran parte in conflitto tra loro. Per procurarsi del cibo, infatti, l'animale deve muoversi nell'ambiente; così facendo, però, si espone a potenziali predatori. Inoltre, trovare e prendere il cibo richiede un'attenzione focalizzata da parte dell'animale e ciò diminuisce la sua vigilanza riguardo ai predatori.
Una possibilità di risoluzione del conflitto dipende dall'abilità di classificare gli oggetti nell'ambiente come potenziali prede o predatori. Questa classificazione può costituire la base per un'azione organizzata e finalizzata, attraverso la quale possano essere evitati i predatori e possano essere catturate le prede. Una delle prime indagini su questo tipo di comportamento è nata dallo studio del sistema visivo della rana compiuto negli anni Cinquanta (Martin, 1994). In questo filone di ricerche si è trovato che le cellule gangliari della retina della rana si possono dividere in quattro classi; ogni classe risponde in modo specifico a caratteristiche particolari dell'ambiente. Sulla base di questa osservazione si concluse che: "in un sistema come questo, una combinazione unica dei quattro contesti qualitativi in una certa relazione spaziale può definire una classe di oggetti [ ... ] Ovviamente questo è un modo in cui gli universali 'preda' e 'predatore' possono essere riconosciuti" (Maturana et al., 1960).
Le risposte delle cellule gangliari fungono da base per classificare l'ambiente. A loro volta, queste classificazioni possono essere usate per produrre un'azione specifica. Un esempio è fornito dal 'rivelatore di insetti'. Le rane rispondono in modo selettivo a oggetti piccoli in movimento, con una risposta di cattura. Questo comportamento è in effetti correlato alle frequenze di scarica di alcune delle cellule gangliari. Perciò, le caratteristiche ottimali nel produrre una risposta da parte di queste cellule sono anche quelle che attivano il comportamento di cattura della preda (Dowling, 1992). Queste cellule si possono quindi considerare come le basi di un 'rivelatore di insetti', che può essere usato per innescare l'azione di afferrare una preda.
Il rivelatore di insetti illustra il fatto che le funzioni cerebrali riguardano la produzione di un comportamento 'dotato di senso'. Ciò che definisce un comportamento dotato di senso viene determinato dal tipo di interazione con l'ambiente in cui quel comportamento ha un ruolo. Per esempio, nell'ambiente naturale della rana, oggetti piccoli in movimento sono molto probabilmente degli insetti. Dunque, il rivelatore di insetti si può considerare come una rappresentazione di una preda contenuta nel cervello della rana. È ovvio che questa è una rappresentazione molto rozza: le rane, infatti, rispondono a qualsiasi oggetto piccolo in movimento come fosse una preda. Al contrario, esse non rispondono a un oggetto fermo anche se è una preda (per esempio, un insetto immobile). Comunque, il cervello della rana categorizza l'ambiente naturale con precisione sufficiente da permettere all'animale di sopravvivere.
La correlazione tra il comportamento e i processi neuronali
Il rivelatore di insetti è un esempio di comportamento che può essere messo direttamente in relazione con le strutture e i processi neuronali sottesi. Cioè, la risposta comportamentale in questo caso può essere direttamente associata ai processi di attivazione delle strutture cerebrali che producono quel comportamento. Sulla base della conoscenza di queste strutture cerebrali e di questi processi si può costruire un modello che mostri in che modo il cervello produce quel comportamento.
Uno degli esempi più approfonditi di questo tipo di modellizzazione del comportamento si trova nel lavoro di W. Heiligenberg (1991), che consiste in una descrizione dettagliata delle reti neuronali con le quali i pesci elettrici localizzano gli oggetti nel loro ambiente. Un pesce elettrico genera di continuo un campo elettrico sinusoidale intorno a sé, per mezzo di un organo speciale situato nella regione caudale. Il pesce avverte il campo per mezzo delle correnti che attraversano la pelle nella parte anteriore del corpo. Un oggetto presente nell'ambiente cambia il campo elettrico prodotto dall' animale, che è in grado così di localizzarne la posizione nell'ambiente. La situazione diventa particolarmente interessante quando l'oggetto presente nell'ambiente è un altro pesce elettrico. Il secondo pesce emette il suo campo sinusoidale che interferisce con il segnale emesso dal primo pesce, e viceversa. Per evitare queste situazioni di interferenza, ogni pesce modula la frequenza del suo segnale in modo da distinguerlo da quello del vicino. Inoltre, un pesce elettrico può in effetti modulare la frequenza di emissione in vari modi, per esempio variando il segnale in modo brusco o graduale cosicché esso funzioni come un mezzo di comunicazione sociale. Dunque, la risposta di 'evitamento dell'interferenza' del pesce elettrico rappresenta uno schema completo di comportamento sociale, che si può mettere direttamente in relazione con un pattern di eventi neuronali (Heiligenberg, 1991).
Dal riflesso all'intelligenza
Il comportamento che abbiamo illustrato nell'esempio precedente può essere caratterizzato come un riflesso, nel senso che esso consiste in una risposta immediata a una stimolazione. In questi casi il comportamento ricade sotto il controllo sensoriale: un particolare stimolo innesca una sequenza di eventi nel sistema nervoso che determina la produzione di una risposta. In un caso come questo la risposta è associata a uno stimolo, il che vuoI dire che verrà prodotta questa particolare risposta ogni qual volta lo stimolo viene presentato. Dunque il comportamento di questo tipo deriva da relazioni stimolo-risposta (S-R).
In un suo autorevole libro D.O. Hebb (1949) argomenta che il comportamento intelligente non è un comportamento di questo genere: "Nei mammiferi, anche inferiori come i ratti, non è stato possibile descrivere il comportamento come diretta interazione fra processi sensoriali e motori; anche nel loro comportamento interviene cioè qualcosa di simile al pensare. Il pensiero propriamente detto comporta senza dubbio un grado di complessità nelle funzioni cerebrali che è di portata troppo rilevante per essere attribuito agli animali inferiori; tuttavia, persino nei ratti è evidente che il comportamento non è completamente controllato da eventi sensoriali immediati e che in esso operano anche processi centrali".
Per considerare questa ipotesi nella giusta prospettiva, ci si deve rendere conto che Hebb scrisse queste parole in un'epoca in cui il comportamentismo era la teoria dominante in psicologia. Secondo questo paradigma teorico, tutto il comportamento deriva da relazioni S-R, o catene di relazioni S-R, e queste si formano attraverso l'apprendimento. Come conseguenza dell'apprendimento, una nuova relazione S-R può rimpiazzare una vecchia. Nel tempo, cioè, una nuova risposta a un dato stimolo può prendere il posto di un'altra. Ma in ciascun momento, la risposta a un dato stimolo è determinata dalla relazione S-R che è presente in quell'istante, come è mostrato negli esempi forniti finora. Quindi, nella teoria comportamentista, il comportamento è sotto il controllo degli stimoli sensoriali. Secondo Hebb, invece, il comportamento intelligente è in minima parte controllato dai processi sensoriali e non è dunque possibile descriverlo in termini di relazioni S-R (o catene di S-R). Non deriva dunque da relazioni S-R (o catene di esse). Piuttosto, tra uno stimolo e una risposta vi è un processo centrale autonomo che contribuisce a determinare la risposta emessa. In particolare, questo processo centrale consiste nella selezione della risposta adeguata da un insieme di risposte possibili. Il processo di selezione della risposta costituisce una forma di attenzione. Poiché interviene tra uno stimolo e una risposta, l'attenzione è di importanza essenziale per il comportamento intelligente e qualsiasi teoria del comportamento intelligente deve tenere conto di questo fattore.
Hebb, allo scopo di fornire una simile "teoria del comportamento basata per quanto possibile sulla fisiologia del sistema nervoso" (Hebb, 1949), formulò il noto concetto di assemblea cellulare, un gruppo distribuito di cellule appartenenti a diverse regioni del cervello, che per breve tempo si strutturano come un sistema chiuso. Un'assemblea cellulare può agire tra lo stimolo e la risposta: infatti, il comportamento intelligente consiste in una sequenza di mediazioni da parte di assemblee cellulari, in cui un insieme di cellule può attivarne altri invece di generare direttamente una risposta. Queste facilitazioni costituiscono il processo dell'attenzione.
Differenza tra riflesso e intelligenza: il livello concettuale
Poiché intervengono tra la percezione e l'azione, i processi centrali autonomi descritti da Hebb consistono in interazioni tra le rappresentazioni che costituiscono la base per la formazione dei concetti. Questi ultimi possono essere visti come una rappresentazione multimodale che può essere attivata da diverse modalità sensoriali. Essi possono essere formati da relazioni (associazioni) tra rappresentazioni sensoriali specifiche che sono distribuite nel cervello (Tanaka, 1996).
La rappresentazione del colore fornisce un esempio di questa ipotesi. I processi cognitivi umani possono elaborare diverse rappresentazioni di un colore come il rosso. Oltre alla rappresentazione visiva attivata dalla lunghezza d'onda della luce rossa, vi sono le rappresentazioni che vengono attivate dalla parola "rosso" pronunciata e dalla parola "rosso" scritta. Queste ultime rappresentazioni sono diverse da quella visiva perché esse sono inizialmente del tutto arbitrarie, il che risulta ovvio se si pensa che vi sono molte lingue diverse con diverse parole e suoni per designare il concetto di "rosso". Queste rappresentazioni linguistiche, comunque, vengono tutte associate alla rappresentazione visiva del colore rosso. Quando queste associazioni sono state formate, le rappresentazioni linguistiche possono evocare il concetto di colore rosso senza dover essere attivate dalla presentazione visiva di questo colore. In questo modo, esse possono formare una rappresentazione concettuale del colore rosso. Le rappresentazioni di questo tipo costituiscono la base dellinguaggio e della cognizione e hanno un ruolo importante nel produrre il comportamento. Per esempio, una persona risulta in grado di selezionare un oggetto rosso su uno schermo sulla base di una istruzione scritta o verbale.
Come ha descritto Hebb, i processi a livello concettuale sono caratteristici del comportamento intelligente umano. Data la loro complessità, Hebb si rese conto che una piena comprensione dei processi autonomi centrali, e quindi del comportamento intelligente, richiede un approccio integrato che metta insieme neuroscienze e psicologia: "Pertanto vi è effettivamente una base razionale che porta a postulare l' esistenza di un fattore nervoso centrale capace di modificare l'azione di ogni singolo stimolo. Il problema teorico consiste nello scoprire le leggi attraverso le quali opera questo fattore. A prima vista sembrerebbe trattarsi di un problema di stretta competenza dei neurofisiologi, ma ad uno sguardo più approfondito si vede che la maggior parte dei dati, utili per formulare queste leggi, sono psicologici o comportamentali. In ultima analisi, il problema è spiegare in che cosa consiste l'attenzione, e per questo si è facilitati se si studia l'attività dell'animale integro. È improbabile che si possa dare una risposta alla questione sopra accennata sulla base dei soli dati fisiologici o dei soli dati comportamentali: è utile invece operare una sintesi corretta di entrambi questi tipi di dati". (Hebb, 1949).
Interazioni tra le rappresentazioni: l'effetto Stroop
Un esempio del contributo della psicologia alla scienza ipotizzato da Hebb è fornito dagli studi condotti sulla natura delle rappresentazioni e delle loro interazioni al livello concettuale. Già IR. Stroop, nel 1935, aveva raccolto dati sperimentali a questo riguardo, utilizzando il paradigma che poi ha preso il suo nome.
La figura (fig. 1) mostra una versione del materiale utilizzato per ottenere l'effetto Stroop (McLeod, 1991). Al soggetto vengono presentate alcune righe di diversi colori o nomi di colori e il suo compito è quello di dire a voce alta i nomi dei colori in ogni riga più velocemente possibile, nel modo delineato in seguito. Quindi la risposta comportamentale richiesta è la stessa in tutti i casi e cioè la produzione verbale dei nomi dei colori. Per questo motivo si usa lo stesso insieme di nomi di colori in ogni riga.
Eppure, malgrado il fatto che si debba produrre lo stesso insieme di nomi di colori, vi sono differenze marcate nei tempi di risposta tra le righe. Già tra le prime due righe si produce una differenza nel tempo di risposta. Nella prima riga i nomi dei colori sono stampati in inchiostro nero, perciò la risposta necessaria in questa riga consiste semplicemente nella lettura delle parole stampate. Nella seconda riga, però, vengono presentati i colori stessi invece dei loro nomi e ciò fa sì che la produzione verbale dei nomi dei colori in questa situazione richieda più tempo rispetto alla lettura diretta delle parole stampate, come nella prima riga. Questa differenza nei tempi di esecuzione del compito si può spiegare in termini di attivazione sequenziale delle rappresentazioni coinvolte. Una parola possiede una rappresentazione linguistica (o lessicale) che viene attivata sia quando essa viene udita o letta sia per produrre quella parola come risposta verbale. Leggere la parola stampata attiva quindi direttamente la rappresentazione lessicale del nome del colore e la risposta verbale può essere prodotta velocemente. Al contrario, se lo stimolo a cui la persona deve rispondere è un quadratino colorato, la rappresentazione visiva del colore deve prima attivare la rappresentazione lessicale del nome del colore, affinché quel nome possa essere prodotto come risposta verbale. Il processo di produzione verbale a partire dalla lettura è quindi un processo più diretto rispetto a quello che provoca la risposta verbale a partire da una percezione visiva.
L'effetto Stroop vero e proprio, comunque, si osserva dalla terza riga in poi. Il compito che produce questo effetto consiste nel nominare i colori dell'inchiostro usato per stampare i nomi dei colori; se invece vengono pronunciati i nomi stampati dei colori, il tempo di risposta è uguale a quello per la prima riga. Si noti che il compito è lo stesso di quello richiesto per la seconda riga: in entrambi i casi vengono presentati dei colori e devono essere pronunciati i loro nomi. Eppure, nella terza riga si ha un significativo aumento del tempo di risposta, non solo rispetto alla prima (come è prevedibile), ma anche rispetto alla seconda.
Il ritardo nel tempo di risposta e gli errori che il soggetto compie derivano dall'interferenza causata dai nomi dei colori stampati nella terza riga. In effetti, nel pronunciare i nomi dei colori dell'inchiostro in questa riga, il lettore può quasi direttamente osservare l'interferenza prodotta dalle parole stampate, anche se cerca di focalizzare l'attenzione solo sui colori. Dunque, malgrado il fatto che essi debbano essere ignorati, i nomi dei colori nella terza riga vengono letti comunque. Di conseguenza, essi attivano le loro rappresentazioni lessicali prima che possano fado le rappresentazioni visive. Per svolgere correttamente il compito, dunque, le rappresentazioni lessicali evocate dai nomi dei colori stampati devono essere soppresse (inibite) per evitare un conflitto con le rappresentazioni lessicali attivate dalla percezione dei colori. Poiché sia le parole stampate sia i colori dell'inchiostro attivano le rappresentazioni lessicali di nomi di colori, il soggetto è costretto a ricorrere a un processo di attenzione selettiva, che da un lato permette di inibire l'accesso della percezione del colore alla relativa rappresentazione lessicale, ma dall'altro causa un incremento del tempo di risposta.
Nella versione del test di Stroop appena descritta, i nomi stampati dei colori creano interferenza quando devono essere nominati i colori dell'inchiostro con cui è scritta la parola, ma l'interferenza non si verifica se la risposta è quella di leggere soltanto i nomi. Come abbiamo descritto sopra, questa differenza deriva dal fatto che vi è un percorso più diretto dalla lettura delle parole alla loro pronuncia, rispetto a quello che porta dalla percezione di un colore alla pronuncia del nome di quel colore, e ciò suggerisce che l'effetto Stroop sia legato al particolare tipo di risposta richiesta. Cioè, se la produzione della risposta favorisse la percezione dei colori rispetto alla lettura dei nomi dei colori, si dovrebbe avere l'effetto opposto: per esempio, se la risposta corretta consiste nel premere un pulsante colorato, i colori degli stimoli creano interferenza se il soggetto deve premere il pulsante del colore corrispondente al nome del colore nella terza riga, ma non viceversa.
Immagini e parole
L'effetto Stroop non si verifica solo con le parole e i colori, ma anche con le immagini e i colori. Per esempio, se il compito consiste nel dare un nome all'immagine di un gatto e insieme all'immagine si presenta una parola come "cane", il tempo di reazione necessario per evocare il nome corretto "gatto" dell'immagine aumenta. Dunque, anche se la parola "cane" non deve essere pronunciata, non viene ignorata e interferisce con la produzione verbale della parola "gatto".
Gli studiosi hanno mostrato che in questo caso l'interferenza deriva principalmente dal fatto che le parole "gatto" e "cane" sono legate semanticamente. Così, la combinazione dell'immagine di un gatto e di una parola come "casa" non produce lo stesso effetto di interferenza osservato con la combinazione dell'immagine del gatto con la parola "cane". Le parole "gatto" e "cane" sono legate semanticamente nel senso che esse appartengono alla stessa categoria degli animali domestici; di conseguenza, le loro rappresentazioni semantiche sono associate e tendono a essere spesso attivate contemporaneamente. Questa associazione, e la tendenza all'attivazione simultanea che essa implica, è all'origine del ritardo nel tempo di latenza poiché l'attenzione selettiva deve inibire una rappresentazione lessicale e favorire l'altra.
Modelli teorici del comportamento intelligente
L'effetto Stroop illustra il modo in cui si possono analizzare la natura delle rappresentazioni e le loro relazioni a livello concettuale, studiando il comportamento che esse producono. L'osservazione delle attività neuronali sotto stanti a questi comportamenti consente di formulare dei modelli precisi che spiegano in che modo il cervello produce questo tipo di comportamento.
Nel caso dei comportamenti riflessi, l'attività cerebrale implicata può essere osservata direttamente, come nel lavoro di W. Heiligenberg (1991) sull' elettro localizzazione nei pesci elettrici. Nel caso del comportamento cosiddetto intelligente, però, la situazione è diversa. Prima di tutto, le strutture neuronali che producono questo tipo di comportamento sono molto complesse e distribuite in varie aree del cervello, il che rende molto difficile (se non impossibile) analizzare in dettaglio gli schemi precisi di attivazione in queste strutture. Inoltre, per ovvie ragioni etiche, l'attività del cervello umano non si può studiare con metodi di indagine diretti e invasivi che si usano nella ricerca su soggetti animali. È importante capire che queste ragioni etiche sono legate strettamente alle differenze qualitative tra il comportamento umano e quello animale. Cioè, possiamo studiare il comportamento animale nel modo in cui lo facciamo proprio perché non ci aspettiamo di trovare (almeno nella loro completezza) quegli stati e quei processi cerebrali che sottendono la cognizione, le emozioni e la coscienza umane.
Fortunatamente, a partire dagli anni Ottanta si sono sviluppate tecniche non invasive per studiare in vivo l'attività cerebrale, come la PET (Positron Emission Tomography, tomo grafia a emissione di positroni), la fMRl (functional Magnetic Resonance Imaging, visualizzazione tramite risonanza magnetica funzionale) e altre ancora. Queste tecniche consentono di visualizzare direttamente l'attività dell' intero cervello mentre questo è impegnato in compiti di vario tipo ed è possibile identificare selettivamente le aree cerebrali coinvolte in particolari compiti (Posner e Raichle, 1994). Però, né la risoluzione spaziale né quella temporale di queste tecniche sono confrontabili con quelle usate nella ricerca su animali. In particolare, metodiche come la PET e la fMRI, al contrario delle classiche tecniche di ablazione chirurgica applicate sugli animali, non forniscono informazioni sul tipo di computazione che ha luogo al livello dei microcircuiti nella corteccia (Douglas et al., 1989).
Dunque, sembrerebbe che le strutture cerebrali implicate nella produzione del comportamento intelligente siano in gran parte 'inaccessibili', nel senso che non si possono osservare direttamente. È importante rendersi conto, comunque, che lo studio delle funzioni cerebrali non è l'unico in cui si presenta questa difficoltà. Vi sono altre scienze che studiano oggetti 'inaccessibili', come la geofisica o l'astronomia. Cionono stante , queste scienze hanno prodotto con successo modelli e teorie precisi circa gli oggetti del loro studio, integrando diversi tipi di informazioni.
L'astronomia come scienza di oggetti inaccessibili
All'inizio del 19° secolo l'astronomia poteva fare poco di più che calcolare la posizione delle stelle nel cielo e la loro magnitudo (luminosità). In un articolo del 1835 il filosofo positivista Auguste Comte argomentava che l'astronomia non sarebbe mai stata capace di fare più di questo. In particolare, l'astronomia non sarebbe stata capace di comprendere la composizione chimica delle stelle, poiché esse sono lontane e inaccessibili: "Il campo della filosofia positiva [cioè la scienza empirica] giace completamente entro i limiti del nostro sistema solare, essendo lo studio dell'universo inaccessibile in qualsiasi senso positivo" (Misner et al., 1973).
È in effetti ovvio che l'Universo sia inaccessibile in qualsiasi senso diretto, non fosse altro che per le distanze coinvolte. Eppure, l'astronomia moderna si è evo Iuta a un livello di gran lunga superiore a quello immaginato da Comte. Questo è sorprendente, se ci si rende conto che l'unica informazione disponibile per gli astronomi consiste nei diversi tipi di radiazioni ricevute dallo spazio esterno. Questa informazione, però, può essere decifrata utilizzando la conoscenza acquisita in fisica circa i modi in cui la radiazione viene prodotta. Per esempio, il modello di atomo sviluppato in fisica quantistica mostra che ogni elemento emette o assorbe radiazioni solo a frequenze particolari, che sono caratteristiche di quell'elemento. Queste frequenze si possono osservare nello spettro della luce emessa da una stella. In questo modo si può identificare la composizione chimica almeno della sfera esterna di una stella.
Inoltre, la fisica ha mostrato in che modo si possano analizzare le proprietà di grandi insiemi di particelle (per esempio, atomi o molecole) in termini statistici. In questo modo si possono formulare modelli che descrivono, per esempio, il movimento degli atomi di un gas. Estendendo queste conoscenze, gli astronomi hanno prodotto modelli che mostrano il modo in cui le stelle si comportano e si evolvono nel tempo.
È importante capire che questo è più di una diretta applicazione delle conoscenze già ottenute in fisica, poiché processi studiati in astronomia hanno luogo su scale non confrontabili con quelle dei processi studiati sulla Terra. Quindi, i modelli e le teorie prodotti in astronomia sono vere e proprie estensioni dei modelli e delle teorie prodotte in fisica.
La matematica nelle scienze empiriche
Le rielaborazioni in campi diversi sono possibili grazie al fatto che i modelli e le teorie in fisica, in astronomia e in altre scienze esatte sono formulati in termini matematici. In effetti, solo dopo l'introduzione di una formalizzazione matematica durante il 17° secolo la fisica ha potuto evolversi nella sua forma attuale. La matematica consente di formulare modelli e teorie in modo non ambiguo; gli stessi, formulati in termini di linguaggio naturale, sono limitati dalle ambiguità caratteristiche del linguaggio naturale. l modelli matematici possono essere studiati analiticamente o numericamente e non solo consentono di descrivere a un livello astratto i fenomeni osservati, ma possono anche gettare luce sul modo in cui questi fenomeni vengono prodotti e successivamente condurre a nuove previsioni. Inoltre, con l'uso dell'analisi matematica si può estendere la validità di un modello, in modo da renderlo applicabile a diversi campi di studio.
Un modello matematico applicato a una scienza empirica è tuttavia profondamente diverso da un modello matematico puro. Il motivo è che una teoria che debba spiegare dati empirici è sempre basata su una selezione tra varie possibilità matematiche, operata su una corretta formulazione dei dati empirici. Per esempio, in astronomia la struttura dell'Universo è descritta dalla teoria generale della relatività, che fornisce una descrizione matematica della struttura dello spazio fisico (più precisamente, dello spazio-tempo) in termini di una geometria a quattro dimensioni. Per secoli, la geometria euclidea (spazio piatto) è stata l'unica teoria disponibile per descrivere lo spazio, mentre in seguito si è scoperto che si potevano formulare in modo matematicamente coerente geometrie con curvatura positiva o negativa. Vi sono quindi, in effetti, tre forme diverse di geometria matematicamente possibili, ognuna delle quali potrebbe fornire una descrizione matematicamente coerente dell'Universo, ma non tutte simultaneamente.
Una teoria matematica dell 'Universo implica quindi la scelta di una fra tre geometrie possibili offerte dalla matematica. Poiché ciascuna geometria è matematicamente consistente, la scelta non può essere compiuta con criteri matematici ma richiede il ricorso a criteri esterni alla matematica stessa, cioè criteri empirici. Tuttavia, anche l'informazione empirica deve essere formulata in termini matematici prima di poter essere utile nella scelta.
Integrazione di diversi tipi di informazione
L'astronomia ha consentito una comprensione dettagliata degli oggetti inaccessibili che studia perché ha integrato tre tipi di informazione. Primo, raccoglie osservazioni empiriche sui fenomeni celesti. Secondo, queste informazioni sono interpretate alla luce delle conoscenze fornite dalla fisica e dalla chimica. Terzo, i modelli che descrivono i fenomeni osservati sono formulati in termini matematici.
Lo studio delle funzioni cerebrali potrebbe applicare l'analogo modus operandi e le neuroscienze cognitive si prefiggono proprio questo scopo, cioè capire come il comportamento venga prodotto da algoritmi eseguiti da strutture neuronali. L'applicazione dei modelli matematici sarà dunque di vitale importanza per integrare su un terreno comune i dati delle neuroscienze e della psicologia e soprattutto lo sarà per lo studio del comportamento intelligente.
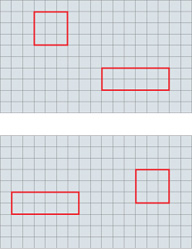
l modelli matematici del comportamento sono computazionali, cioè in grado di identificare le variabili che regolano un certo fenomeno e ne descrivono le interazioni secondo funzioni matematiche. Per mostrare in che modo il cervello produce un processo cognitivo, questi modelli dovranno riferirsi ai processi di attivazione osservati nelle strutture neuronali. Dovranno però anche soddisfare i requisiti computazionali necessari per produrre un comportamento cognitivo. Questi requisiti sono ancora oggetto di studio (Newell, 1990), ma uno di essi, che riguarda il modo in cui l'informazione è utilizzata e immagazzinata in un modello, può essere formulato come segue. Si possono distinguere due categorie di informazione: da un lato, quella utilizzata e immagazzinata in memoria in modo permanente, dall' altro, quella che viene usata e immagazzinata solo temporaneamente. Il primo tipo di informazione rappresenta la conoscenza 'permanente' che il modello deve possedere per produrre il comportamento. Nel caso della visione, per esempio, è utile conservare stabilmente l'informazione sull'identità dei vari oggetti percepiti in una scena (alberi, case, automobili, ecc.), poiché tali oggetti si possono incontrare di frequente. Il secondo tipo di informazione, invece, rappresenta la conoscenza momentaneamente necessaria al modello per poter essere efficiente. Nell'esempio della visione, possiamo immaginare che le relazioni variabili tra gli oggetti (per esempio, il fatto che l'albero sta di fronte alla casa, o che la macchina si trova alla sinistra dell' albero) rientrino in quest'ultimo tipo di informazioni. Nella maggior parte dei casi (tranne alcune eccezioni), tuttavia, non ha molto senso memorizzare a lungo questa informazione, poiché le relazioni tra gli oggetti possono facilmente cambiare nella stessa scena o in scene diverse.
Per la sua importanza, il resto di questo saggio è dedicato a questo argomento, a partire da una breve discussione sulla teoria della computazione.
La teoria della computazione come matematica del comportamento
l modelli computazionali sono stati introdotti nelle scienze comportamentali a partire dagli anni Sessanta, quando il cognitivismo rimpiazzò il comportamentismo come teoria dominante in psicologia. In effetti, però, vedremo che anche il comportamentismo usava certi modelli computazionali per descrivere il comportamento.
La teoria della computazione nacque intorno al 1936 come una branca della matematica che studiava le funzioni che possono essere prodotte dalle cosiddette procedure efficaci, o algoritmi. Questi ultimi si possono descrivere informalmente come procedure che operano in modo riproducibile e intenzionale (von Neumann, 1988). Questa definizione informale mostra il motivo per cui i modelli computazionali sono dei buoni candidati per descrivere i processi cognitivi: anche i processi cognitivi operano in modo riproducibile e intenzionale, nel senso che essi consentono all'organismo di interagire con il suo ambiente in modo significativo (per esempio, trovare le prede ed evitare i predatori).
La nozione di 'efficace' implica che le procedure possano essere generate da macchine. La teoria della computazione si può infatti definire partendo da questa prospettiva. Si può così dire che essa studia la natura delle funzioni che possono essere prodotte dalle macchine. Oppure, al contrario, che studia la natura delle macchine che producono delle funzioni. La teoria della computazione ha dimostrato l'esistenza di una grande varietà di macchine che possono produrre funzioni computabili. Eppure, le funzioni prodotte da tutte le macchine appartengono allo stesso insieme di funzioni. Questo insieme è noto come l'insieme delle funzioni computabili (o ricorsive). Una macchina, quindi, può produrre l'intero insieme di funzioni computabili, o può produrre solo un sottoinsieme di funzioni di questo insieme. In questo modo, l'insieme delle funzioni computabili può essere usato solo per confrontare macchine che a prima vista sembrano differenti: due macchine sono funzionalmente equivalenti se producono lo stesso sottoinsieme di funzioni computabili. Inoltre, l'insieme delle funzioni che può essere prodotto da una macchina caratterizza la produttività computazionale di quella macchina.
Il fatto che lo stesso sottoinsieme di funzioni possa essere prodotto da diverse macchine ha suggerito la distinzione tra l'algoritmo e l'implementazione dell'algoritmo. Un algoritmo è una descrizione delle operazioni necessarie per produrre una funzione computabile, mentre la implementazione di un algoritmo riguarda il modo in cui l' algoritmo può essere eseguito su una particolare macchina. In altre parole, lo stesso algoritmo può essere eseguito su diverse macchine, cioè può essere realizzato in modi diversi.
Poiché l' algoritmo descrive le operazioni necessarie per produrre una funzione computabile, gli psicologi cognitivi assumono che i modelli del comportamento consistano in algoritmi. Secondo questa concezione, le questioni relative alla realizzazione materiale di un algoritmo non sono importanti per lo psicologo (Fodor e Pylyshyn, 1988). Si noti, comunque, che questa visione è basata sulla ipotesi che il comportamento possa essere descritto adeguatamente in termini di funzioni. L'indifferenza degli psicologi per il so strato materiale delle informazioni, che ha dominato la psicologia cognitiva per decenni, ha altresì ostacolato l'integrazione di quest'ultima con le neuroscienze; per questo motivo descriverò brevemente la relazione tra il comportamento e le funzioni (van der Velde, 1996).
Funzioni e comportamento
Una funzione consiste in una relazione tra due variabili numeriche, per esempio y = 2x. Questa funzione è computabile perché può essere prodotta da una macchina, cioè una macchina può produrre una rappresentazione del numero y quando le viene presentata una rappresentazione del numero x. Le funzioni e il comportamento sono in qualche modo isomorfi, se si assume che la formula y = f(x) esprime il fatto che la risposta y è funzione dello stimolo x. In questo modo, il comportamento diventa descrivibile in termini di algoritmi che producono una risposta quando viene presentato uno stimolo. Un esempio di questo procedimento è fornito dal rivelatore di insetti della rana che abbiamo descritto all'inizio di questo saggio. L'input di questa funzione è rappresentato da un piccolo oggetto in movimento e il suo output è la risposta consistente nella cattura dell'oggetto.
Questo esempio, comunque, illustra anche una differenza importante tra le funzioni computabili e il comportamento. Un comportamento efficace dipende anche dalla velocità con cui viene prodotta una risposta. Affrnché il rivelatore di insetti sia efficace, esso non deve solo produrre la risposta giusta allo stimolo pertinente, ma deve anche produrla entro un particolare intervallo di tempo. La velocità di elaborazione in quanto tale manca nella nozione di funzione matematica, poiché questa è solo una relazione tra numeri, ovvero tra una variabile che rappresenta l'input e un'altra che rappresenta l'output. La valutazione dell'efficacia di un algoritmo si limita quindi alla precisa corrispondenza, specificata dalla funzione, tra un certo input e un certo output e non riguarda la velocità con cui questa funzione viene calcolata. La velocità di elaborazione è un aspetto che attiene solamente all'implementazione concreta dell'algoritrno, ma essa influenza ovviamente l'efficacia del comportamento osservato.
L'importanza della velocità di elaborazione nella descrizione del comportamento mostra che le questioni riguardanti l'implementazione sono importanti per la psicologia. Gli algoritmi in sé possono dare solo una descrizione incompleta della produzione del comportamento, poiché essi descrivono la relazione funzionale tra uno stimolo e una risposta, ovvero il tipo di operazioni necessarie per produrre una risposta. Per dare però una descrizione adeguata del comportamento, un algoritmo si deve combinare con una descrizione della velocità con cui viene eseguito. Una simile combinazione si può realizzare attraverso la simulazione su computer di reti neuronali artificiali (van der Velde, 1996).
Due tipi di macchine
Come abbiamo già notato, la produttività computazionale delle macchine è caratterizzata dal (sotto )insieme di funzioni computabili che esse possono produrre. La produttività di due macchine può differire per diversi motivi, ma un punto è di particolare importanza ai fini della formulazione di modelli del comportamento, e riguarda la differenza tra i cosiddetti automi a stati finiti (ASF) e le macchine come la macchina di Turing. Una macchina di Turing consiste in un ASF connesso a una memoria di lavoro che elabora l'informazione di utilità immediata.
Un ASF è una macchina che possiede un numero finito di stati interni distinguibili. Esso calcola funzioni per mezzo delle transizioni tra i suoi stati interni (Minsky, 1967). Gli automi sono risultati utili per creare modelli del comportamento, soprattutto per rappresentare modelli di tipo comportamentista. Secondo questo paradigma teorico, si può descrivere il comportamento in termini di associazioni stimolo-risposta. In una forma semplice di associazione S-R, uno stimolo produrrà direttamente una risposta, ma in forme più complesse la risposta prodotta può dipendere anche dalla storia recente. lnfatti, uno stimolo precedente potrebbe aver prodotto una risposta 'latente', ovvero un cambiamento dello stato interno dell'organismo. In questo modo, una sequenza di stimoli può indurre una sequenza di cambiamenti di stati interni nell'organismo, nella forma di una catena di relazioni S-R, la quale determina la risposta data allo stimolo attuale. Questi processi riflettono le transizioni tra gli stati interni di un automa a stati finiti.
Per spiegare il comportamento complesso, tuttavia, bisogna ipotizzare un enorme numero di catene S-R variamente interconnesse fra loro, come avviene nella teoria dello psicologo comportamentista C. Rull. Ora, come hanno notato A. Amsel e M.E. Rashotte (1984): "Mentre gli articoli [di Rull] sono brillanti da molti punti di vista, al lettore moderno sollevano ancora una volta la domanda assillante sul fatto che una descrizione analitica di tipo S-R del comportamento complesso sia percorribile. [ ... ] il solo numero di legami associativi e il problema di quantificare il loro stato momentaneo individuale e combinato per prevedere il comportamento bastano a confonderci la mente".
La psicologia cognitiva ha abbandonato gli ASF e le associazioni S-R come modelli adeguati per descrivere il comportamento, e usa invece a questo scopo macchine come la macchina di Turing. La macchina di Turing è in effetti un automa a stati finiti connesso a una memoria di lavoro arbitrariamente grande che prende la forma di un nastro virtualmente infinito. L'automa contiene il programma della funzione da computare, ma la memoria di lavoro viene usata nella esecuzione del programma. A questo fine, la macchina può effettuare operazioni sulla memoria, come la ricerca e l'immagazzinamento di simboli. Essa calcola così una funzione per mezzo di interazioni tra un programma e una memoria di lavoro. Queste interazioni si possono definire come manipolazioni di simboli.
Il fatto che la cognizione derivi da una manipolazione di simboli è stato un dogma centrale della psicologia cognitiva (Fodor e Pylyshyn, 1988), ma questo implica che sia il cervello a effettuare una forma di manipolazione di simboli. In altre parole, nelle strutture cerebrali che producono un comportamento intelligente si dovrebbe poter rintracciare una distinzione tra 'programmi' e 'memorie di lavoro'. Questa ipotesi viene formulata in modo chiaro da A. Newell (1980), che fa notare anche la mancanza di integrazione tra le neuroscienze e la psicologia cognitiva da questo punto di vista: "Questa è una vera previsione sulla struttura del sistema nervoso, e dovrebbe alla fine ispirare lo sforzo di capire in che modo il sistema nervoso funzioni. Questo non sembra essere successo [ ... ]. Infatti, non sono a conoscenza di alcuna discussione su questo argomento nella letteratura in neuroscienze".
Il motivo per cui gli psicologi cognitivisti hanno cominciato a nutrire interesse per l'intelligenza artificiale e per la macchina di Turing risiede nella produttività computazionaIe di queste macchine. Le macchine virtuali che, come nel modello di Turing, prevedono due stadi separati per l'elaborazione dell'informazione (il programma e la memoria di lavoro) costituiscono una rivoluzione nella teoria della computazione, poiché dimostrano che modelli apparentemente semplici da un punto di vista strutturale possono simulare funzioni enormemente complesse e possedere, perciò, un'enorme produttività. Prima di entrare nel dettaglio di questa discussione, illustrerò l'importanza della produttività computazionale per la psicologia cognitiva.
L'uso produttivo della conoscenza nella cognizione
L'uso produttivo della conoscenza è una caratteristica della cognizione in generale e si può trovare, per esempio, nella comprensione del linguaggio e nella elaborazione visiva. La somiglianza, da questo punto di vista, tra la comprensione del linguaggio e l'elaborazione visiva è descritta in modo chiaro da M.l. Sereno (1991): "L'integrazione di viste successive nella comprensione di una scena visiva richiede una specie di operazione di montaggio seriale, simile da alcuni punti di vista alla integrazione dei significati delle parole nella comprensione del parlato. l primati (ma anche molti altri animali) fanno lunghe serie di fissazioni al ritmo di diverse nuove viste al secondo durante la comprensione di una scena. Ogni fissazione porta la retina ad una nuova parte della scena visiva e genera una raffica di attività in VI, che rimpiazza in gran parte la raffica causata dalla fissazione precedente. Le aree visive superiori con retinotopia meno precisa integrano in qualche modo le informazioni provenienti da queste sequenze separate di attività, in modo da generare una rappresentazione interna della posizione e della identità degli oggetti rilevanti nella scena attuale (per esempio, predatori, pezzi di cibo, particolari individui appartenenti alla stessa specie, vie di fuga, alberi adatti per dormire, ecc.) che possono servire come base per l'azione".
Nel caso della comprensione del linguaggio, il significato di una frase può essere elaborato sulla base del significato delle sue singole componenti (le parole) e della sua struttura. La struttura di una frase si può analizzare nei termini delle regole grammaticali che determinano il linguaggio. Sia l'insieme delle parole sia quello delle regole sono insiemi limitati, eppure essi possono essere combinati in modo da generare un insieme illimitato di frasi, che possono essere utilizzate per veicolare una quantità virtualmente infinita di informazione. Il fatto che l'insieme delle parole e quello delle regole grammaticali siano limitati è essenziale. Solo in questo modo essi possono essere immagazzinati come conoscenza permanente. Sulla base di questa quantità limitata di conoscenza, però, l'utente di un linguaggio può produrre una quantità di informazione potenzialmente illimitata. Questa capacità costituisce la produttività della comprensione (e della produzione) del linguaggio.
L'uso produttivo della conoscenza nella elaborazione visiva consiste nella capacità di identificare oggetti e scene visive mai visti prima, come le strade e gli edifici di una città sconosciuta. Le scene e gli oggetti non familiari spesso consistono in composizioni di oggetti più elementari, organizzati in un ordine particolare. In questo modo un oggetto o una scena non familiari possono essere una composizione nuova di componenti familiari, o una composizione familiare di nuovi componenti. Nel primo caso, l'oggetto o la scena possono essere identificati sulla base dei suoi elementi familiari. Nel secondo caso, la composizione familiare può aiutare nella identificazione dei componenti.
Rappresentazioni implicate nell'identificazione di oggetti
Per comprendere l'uso produttivo della conoscenza nella elaborazione visiva, si consideri il compito di costruire una macchina che possa identificare oggetti su uno schermo. La capacità di questa macchina può essere misurata solo dalla sua risposta comportamentale. Così, per esempio, essa avrà identificato un oggetto se potrà produrne il nome corretto (l'etichetta), o se può puntare o raggiungere l'oggetto sullo schermo. La macchina può produrre questo comportamento solo se possiede un magazzino di memoria delle rappresentazioni degli oggetti che deve identificare. Ogni rappresentazione può essere vista come uno stato interno della macchina che viene attivato dall'oggetto rappresentato e che è necessario per produrre comportamenti appropriati per ciascun oggetto (per esempio, dare nomi diversi a oggetti diversi). Se vi è soltanto uno stato interno nella macchina, essa può produrre solo un tipo di comportamento (per esempio, dare lo stesso nome a tutti gli oggetti).
Un oggetto presente nel campo visivo consiste spesso in una combinazione di attributi come forma e colore. Vi sono due tipi di rappresentazioni che una macchina può usare per identificare correttamente un oggetto cioè, per esempio, identificare un triangolo rosso come tale, e non solo come un triangolo o come un oggetto rosso. Il primo consiste in rappresentazioni di combinazioni specifiche di attributi. In questo modo, la macchina identificherà un triangolo rosso poiché possiede una rappresentazione della specifica combinazione di rosso e di triangolo. Il secondo tipo consiste in rappresentazioni dei singoli attributi. In questo caso, la macchina possiede una rappresentazione del colore rosso e una del triangolo, ma non una rappresentazione della loro combinazione. Quando incontra un triangolo rosso, la macchina può identificare l'oggetto integrando le rappresentazioni del rosso e del triangolo, cioè 'sa' che vi sono un oggetto rosso e un triangolo nel campo visivo e 'sa' che questi oggetti sono in effetti lo stesso.
In apparenza, il primo tipo di processo sembra il modo più semplice per risolvere il problema dell'identificazione degli oggetti. Un oggetto può attivare immediatamente la sua rappresentazione, che può generare a sua volta una risposta. Non è necessaria un'operazione che combini le rappresentazioni dei singoli attributi per generare una risposta. In effetti, una tale operazione comporta difficoltà considerevoli e ciò risulta chiaro quando vi sono due o più oggetti sullo schermo. Supponiamo per esempio che lo schermo contenga un triangolo rosso e un quadrato blu. Se l'identificazione è basata sulla rappresentazione di singoli attributi, le rappresentazioni del rosso, del blu, del triangolo e del quadrato sono attive; ma queste stesse rappresentazioni sarebbero attive se sullo schermo vi fossero un triangolo blu e un quadrato rosso. Dunque, al livello delle singole rappresentazioni, non si possono distinguere combinazioni diverse degli stessi attributi. A questa difficoltà ci si riferisce spesso come al binding problem (problema del legame), poiché riguarda il problema di come le rappresentazioni di singoli attributi si possano combinare per un oggetto (Treisman, 1996).
Sebbene l'identificazione degli oggetti a partire da rappresentazioni composite già presenti in memoria non soffra del binding problem, un processo di questo tipo presenta comunque alcune difficoltà. Un primo ostacolo riguarda il numero di rappresentazioni da immagazzinare in memoria: anche con un insieme limitato di colori e di forme si può costruire un numero enorme di combinazioni e memorizzarle tutte una per una costituirebbe un impegno cognitivo molto costoso. Questa esplosione combinatoriale diventa ancor più grave se si considera il fatto che esistono molti altri attributi che caratterizzano un certo oggetto, come la velocità, la direzione di movimento e la posizione. Anche questi attributi devono essere noti per produrre un'azione particolare.
Identità e posizione
Per prendere o evitare un oggetto, è necessario conoscerne non solo l'identità ma anche la posizione. Di nuovo, se un sistema (naturale o artificiale) possiede rappresentazioni separate dell'identità e della posizione di un oggetto, ma non una rappresentazione sintetica di questi attributi, si presenta un binding problem paragonabile a quello per la forma e il colore. D'altro canto, se vengono prodotte rappresentazioni composite, si incorre nel rischio dell'esplosione combinatoriale delle possibilità.
La combinazione dell'identità e della posizione pone una seconda (e fondamentale) difficoltà che deriva dall 'uso di sole rappresentazioni congiunte. Si consideri il problema di riconoscere un oggetto familiare in una posizione in cui non era mai stato visto prima. In questo caso, se assumiamo che le rappresentazioni siano generate attraverso l'esperienza, la macchina potrebbe non possedere la specifica rappresentazione sintetica dell'oggetto visto in quella data prospettiva, e quindi non lo riconoscerà. In altre parole, la macchina tratterà questo oggetto come un oggetto nuovo, per il quale deve generare una nuova rappresentazione. Lo stesso si verifica per qualsiasi nuova combinazione di forme, di colori (o altri attributi) familiari. Così, per esempio, questa macchina potrebbe conoscere i triangoli rossi e i quadrati blu senza sapere nulla dei triangoli blu e dei quadrati rossi.
Sistematicità, composizionalità e produttività
Il riconoscimento visivo, o l'identificazione di un oggetto sulla base della congiunzione di rappresentazione, non si risolve solo in una esplosione combinatoriale di rappresentazioni, ma anche in una mancanza di sistematicità e ciò vuoI dire che ogni evento visivo (per esempio, un oggetto in una certa posizione) viene trattato come un evento isolato. Abbiamo già illustrato questo fatto con l'esempio della identificazione dello stesso oggetto in diverse posizioni. Invece di riconoscere che esiste una relazione tra questi eventi percettivi, nel senso che essi rappresentano lo stesso oggetto in diverse posizioni, le prospettive di un oggetto vengono trattate da questa macchina come oggetti diversi. Lo stesso si verifica per le combinazioni di forme e di colori. In questa macchina, un triangolo blu e un triangolo rosso sono altrettanto diversi tra loro che un triangolo blu e un quadrato rosso, poiché la macchina 'non capisce' che i triangoli blu e rossi sono accomunati dal fatto di essere la stessa forma con diversi colori.
L'incapacità di una macchina di questo tipo di comprendere le relazioni sistematiche tra eventi visivi è una conseguenza diretta della natura delle sue rappresentazioni: se le sintesi fra gli attributi visivi sono contenute in rappresentazioni specifiche, le relazioni tra gli eventi visivi vengono perse. Le relazioni tra diverse rappresentazioni sintetiche si perdono perché le rappresentazioni stesse non hanno una struttura interna che si possa usare per codificarle. Al contrario, tutto ciò che rimane è un insieme, o una lista, di rappresentazioni individuali.
La psicologia cognitiva ha accettato il criterio della sistematicità rappresentazionale come un elemento chiave per produrre un comportamento intelligente. Secondo lA. Fodor e Z.W. Pylyshyn (1988): "Le capacità cognitive si presentano in gruppi strutturalmente organizzati; la sistematicità è una loro caratteristica pregnante. Esiste ogni prova del fatto che la mente non può essere frazionata in unità indipendenti". Un altro termine usato per denotare la sistematicità dei processi cognitivi è composizionalità, il quale sta a indicare che la maggior parte delle rappresentazioni mentali sono composte a partire da rappresentazioni più elementari, come le parole che compongono una frase. In effetti, le diverse nozioni di sistematicità, composizionalità e produttività denotano tutte lo stesso fenomeno (Fodor e Pylyshyn, 1988).
La sistematicità rappresentazionale si può realizzare sulla base delle relazioni tra rappresentazioni e una sintesi di attributi emerge dalle relazioni tra le rappresentazioni dei singoli attributi. In questo modo si usano produttivamente le rappresentazioni, poiché sulla base degli stessi elementi fondamentali si possono identificare eventi diversi in termini di relazioni tra le singole rappresentazioni. Supponiamo quindi che un particolare oggetto (per esempio, un triangolo) si presenti in diverse posizioni. Nell'approccio sistematico, sarà identificato come lo stesso oggetto, poiché per quell' oggetto viene usata la stessa rappresentazione (di identità) nel processo di identificazione. L'oggetto sarà anche identificato come localizzato in diverse posizioni, a causa delle relazioni tra la rappresentazione dell'identità dell'oggetto e le rappresentazioni delle diverse posizioni nelle quali viene presentato.
L'uso produttivo delle rappresentazioni nello scanning visivo
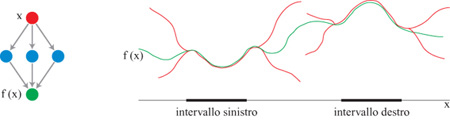
Il valore produttivo delle rappresentazioni può essere dimostrato prendendo spunto dagli esperimenti di scanning (letteralmente, scansione) visivo. In questo caso, l'identità di un oggetto sullo schermo è nota e se ne deve trovare la posIzIOne attraverso un processo di attenzione selettiva, poiché bisogna individuare l'oggetto in mezzo a un certo numero di stimoli irrilevanti, detti distrattori. Quando la discriminazione deve essere fatta sulla base della posizione di uno stimolo che appare in una porzione prefissata del campo visivo, allora si parla di attenzione selettiva spaziale. Come ha descritto Hebb (1949), i processi attenzionali sono di importanza cruciale per la produzione di un comportamento intelligente.
L. Chelazzi e i suoi collaboratori hanno condotto un esperimento sul comportamento di scanning visivo, in cui dapprima si mostrava a una scimmia un oggetto visivo familiare (per esempio, un triangolo) come stimolo target al centro del punto di fissazione (Chelazzi et al., 1993). L'oggetto quindi scompariva per un breve intervallo, durante il quale la scimmia doveva mantenere l'oggetto in memoria. Al termine dell'intervallo venivano mostrati due oggetti, uno dei quali era lo stimolo target e l'altro un distrattore (per esempio, un quadrato). Entrambi gli oggetti venivano presentati in una posizione periferica del campo visivo e il compito della scimmia era di produrre un movimento dell'occhio per riportare lo stimolo corretto (il triangolo) al centro del campo visivo.
Durante questo esperimento veniva misurata l'attività delle cellule nella corteccia infero-temporale (lT). l risultati dimostravano che, dopo un certo numero di presentazioni, ciascun oggetto attivava una differente popolazione di cellule nella corteccia lT e perciò, quando l'oggetto veniva presentato come stimolo target prima dell'intervallo, veniva attivato selettivamente il gruppo di cellule corrispettivo. Durante il periodo di intervallo l'attività di queste cellule diminuiva, senza però tornare al livello di riposo precedente alla stimolazione. La presentazione successiva dello stimolo insieme al distrattore aumentava inizialmente sia l'attività della popolazione che codificava il target, sia l'attività della popolazione che codificava il distrattore.
Nella maggior parte dei casi, però, la risposta di attivazione allo stimolo target era più alta, a causa della attività sostenuta durante il periodo di intervallo. Dopo una prima attività di scarica contemporanea, l'attività delle cellule che codificavano il distrattore diminuiva, mentre le cellule che codificavano il target rimanevano attive. Il movimento oculare verso l'oggetto target avveniva molti millisecondi dopo l'inibizione delle cellule sensibili al distrattore. Dunque, lo stimolo corretto, che la scimmia doveva individuare, veniva presentato due volte in questo esperimento, ma in posizioni diverse. Eppure esso induceva l'attivazione dello stesso insieme di cellule nella corteccia lT e ciò indica che queste cellule costituiscono una rappresentazione di identità dell'oggetto indipendente dalla sua posizione. In altre parole, il target e il distrattore non sono codificati simultaneamente in termini di identità e posizione e, ciononostante, l'animale sapeva produrre il movimento corretto dell' occhio per riportare il target al centro del campo visivo. Dunque l'animale poteva attivare una rappresentazione contenente l'informazione relativa alla posizione dello stimolo desiderato nel campo visivo e ciò accadeva dopo una competizione tra le cellule della corteccia lT, necessaria ad attivare selettivamente l'insieme di cellule sensibili allo stimolo corretto.
Si noti, comunque, che l'attivazione di una rappresentazione di identità non risolve ancora il problema di trovare la posizione dello stimolo: se l'oggetto e le varie posizioni che esso può assumere nel campo visivo sono rappresentati in modo indipendente, una selezione tra le rappresentazioni di identità non influenza le rappresentazioni delle posizioni. L'animale deve quindi ancora risolvere il problema di trovare la rappresentazione della posizione connessa alla rappresentazione di identità dello stimolo target. In altre parole, l'animale deve fare fronte al binding problem, il quale può perciò essere visto come una conseguenza dell'uso produttivo delle rappresentazioni. Per comprendere come possa essere risolto il binding problem, è necessario capire la nozione di produttività in termini computazionali.
Produttività in termini computazionali
L'uso produttivo delle rappresentazioni, come l'abbiamo illustrato, è caratteristico dei sistemi computazionali in cui vige una distinzione funzionale tra programma e memoria di lavoro, di cui la macchina di Turing costituisce un esempio. Per questo motivo, e per il fatto che non vi è una macchina computazionalmente più potente, la macchina di Turing viene spesso usata in psicologia cognitiva come esempio di produttività computazionale. Dal punto di vista degli psicologi cognitivi, questo non implica però che il cervello corrisponda esattamente a una macchina di Turing, come esprimono chiaramente Fodor e Pylyshyn (1988): "I modelli della mente [in psicologia cognitiva] venivano dedotti dalla struttura delle macchine di Turing e von Neumann. Ovviamente, essi non sono aderenti ai dettagli di queste macchine nel modo in cui vengono esemplificati nella formulazione originale di Turing o in computer commerciali tipici, ma solo l'idea fondamentale che il genere di computazione rilevante al fine di comprendere la cognizione coinvolga delle operazioni su simboli".
Il concetto di operazione su simboli si riferisce alla interazione tra il programma e la memoria di lavoro nelle macchine come quella di Turing. Dunque, l'uso produttivo delle rappresentazioni è equivalente a operare su (o manipolare) simboli. In effetti, i simboli sono rappresentazioni immagazzinate nella memoria di lavoro e il programma manipola questi simboli durante l'interazione tra il programma e quella memoria. Vi sono vari esempi espliciti di queste interazioni (van der Velde, 1996; 1997). Illustrerò qui la differenza tra le macchine come quella di Turing e gli ASF in modo più informale.
I modelli ASF rappresentano sistemi che sanno gestire problemi computazionali in cui la quantità di informazione da elaborare è costante per diverse istanze del problema. L'uso produttivo delle rappresentazioni (e quindi la manipolazione dei simboli), d'altra parte, è necessario per quei problemi di computazione in cui la quantità di informazione da elaborare cresce per diverse istanze del problema. Per fare un primo esempio, si consideri la differenza tra l'addizione e la moltiplicazione. Nella figura (fig. 2) si confrontano l'addizione e la moltiplicazione dei numeri 55 e 76 con l'addizione e la moltiplicazione dei numeri 555 e 876.
L'addizione di due numeri si può sempre rappresentare con tre righe: due righe che rappresentano i due numeri da addizionare e una che rappresenta il risultato. In particolare, questa rappresentazione non cambia anche se i numeri da addizionare diventano più grandi. In quel caso le righe si allungano, ma il processo si può ancora rappresentare con tre righe. Al contrario, la moltiplicazione di due numeri non può sempre essere contenuta in tre righe; in effetti, non può essere rappresentata con nessun numero fisso di righe. Di nuovo, due righe sono necessarie per rappresentare i numeri da moltiplicare e una riga per rappresentare il risultato. Ma, tra queste, è necessario un altro insieme di righe.
Queste righe intermedie rappresentano i prodotti parziali, come 6x55 e 70x55 nella figura 2, che si devono calcolare prima di poter produrre il risultato finale. Queste righe intermedie rappresentano l'informazione che deve essere immagazzinata temporaneamente durante il processo di calcolo dellamoltiplicazione. Il numero di righe intermedie però cresce quando si devono moltiplicare numeri più grandi. Questo aumento rappresenta il fatto che, quando devono essere moltiplicati numeri grandi, aumenta la quantità d'informazione temporanea che deve essere elaborata.
Nel caso dell'addizione, invece, la quantità di informazione necessaria per il processo di computazione rimane costante anche per numeri arbitrariamente grandi e questo deriva dal fatto che l'informazione di livello intermedio rimane costante. Questa informazione consiste nel 'riporto' che si produce quando si addizionano due numeri. Per esempio, consideriamo l'addizione di figura 2; dapprima eseguiamo 5 + 6 = 11: si ha come output (cioè, nel caso più comune si scrive) la cifra l più a destra, mentre la cifra l più a sinistra si deve riportare alla coppia seguente 5 + 7, in modo da dare 1 + 5 + 7 = 13. Si può quindi scrivere il numero 3, e si deve riportare la cifra l alla coppia seguente, se è presente. Questo processo si ripete per tutti i numeri da addizionare. I numeri da riportare rappresentano l'informazione che deve essere immagazzinata temporaneamente durante il calcolo dell'addizione, ma la cifra da riportare viene addizionata solo alla coppia seguente di numeri e deve quindi essere immagazzinata solo durante l'addizione di questa coppia, dopo di che può essere rimossa dalla memoria e rimpiazzata dal nuovo riporto, se ne esiste uno. La quantità di informazione non cresce quindi col crescere dei numeri: essa si limita sempre al riporto di una cifra da una coppia di numeri a quella successiva.
Un automa a stati finiti come pianificatore esaustivo di casi
Poiché la quantità di informazione necessaria per addizionare due numeri rimane costante per tutte le coppie di numeri, il processo dell'addizione si può realizzare attraverso un ASF. Affinché un ASF calcoli una certa funzione, esso deve possedere uno stato interno distinguibile per ogni caso che può incontrare. Si consideri il caso dell'addizione di due numeri binari, per esempio 101 + 111 = 1100. Si ipotizzi che i numeri vengano presentati al sistema simultaneamente una cifra alla volta, a partire dalla cifra meno significativa, allo scopo di non gravarlo con un immagazzinamento che risulterebbe impossibile per numeri arbitrariamente grandi. Poiché i numeri binari sono composti a partire da due soli simboli, nell'addizionare due cifre isolate si danno solo tre diverse combinazioni: 0 + 0 = 0, 0+ 1 = 1 +0= 1, e 1 + 1 = 10. La combinazione 1+1=10 significa che si produce 0 in output e l è il riporto alla coppia seguente di cifre. L'eventualità di un simile riporto vuoI dire che si possono presentare sei diversi casi nel calcolo binario, che derivano dall'addizionare un riporto di 1 o 0 (cioè nessun riporto) a ognuna delle tre combinazioni descritte sopra. l diversi casi rappresentano la conoscenza necessaria per computare l'addizione.
Nell'addizione di due numeri binari si presentano sempre gli stessi sei casi e ciò mostra che la conoscenza necessaria per addizionare due numeri arbitrariamente grandi rimane costante.
Un automa progettato per addizionare numeri binari deve possedere uno stato definito (cioè diverso) per ognuno dei sei casi che si possono presentare durante il calcolo (van der Velde, 1997). Dunque, tale automa è una forma di pianificazione esaustiva di casi possibili. In termini rappresentazionali, un ASF deve possedere una rappresentazione per ogni caso che si può presentare e perciò la soluzione di un problema computazionale da parte di un automa a stati finiti consiste in un'esplosione combinatoriale di rappresentazioni. L'automa alla fine fallirà se non possiede una rappresentazione per ogni caso che si può presentare. Questo è il motivo per cui un simile modello non può moltiplicare numeri arbitrariamente grandi. In questo caso, la quantità di informazione da elaborare cresce con il crescere dei numeri, come è descritto nella figura 2, mentre la procedura è, in effetti, sempre la stessa, poiché si può applicare lo stesso insieme di regole per qualsiasi moltiplicazione di due (o più) numeri. Quindi, sebbene la quantità di informazione da elaborare cresca in questo problema computazionale, esso può essere risolto dallo stesso insieme di regole.
Una macchina come quella di Turing (o un computer digitale) eseguirebbe la moltiplicazione usando il suo programma per immagazzinare le regole e la sua memoria di lavoro per immagazzinare la quantità crescente di informazione da elaborare durante la computazione. Poiché un programma su una macchina di Turing è un automa a stati finiti, il programma può immagazzinare solo un insieme finito di regole ma, nel caso della moltiplicazione, si può usare in effetti lo stesso insieme di regole per qualsiasi computazione. Per effettuare un dato calcolo, la memoria di lavoro deve essere abbastanza grande affrnché il programma possa interagire con essa durante il processo (van der Velde, 1997).
Interazione tra programma e memoria nel riconoscimento di stringhe di parentesi
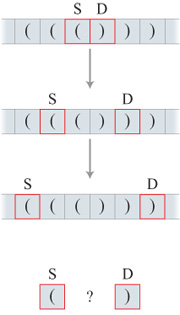
L 'interazione tra il programma e la memoria interviene in casi come quello del riconoscimento di stringhe di parentesi. Nella figura (fig. 3) si mostrano due diverse categorie di stringhe, entrambe dette ben formate poiché contengono un numero uguale di parentesi aperte e chiuse nel giusto ordine. Il primo tipo di stringa consiste in una sequenza di parentesi aperte e chiuse alternate. Il riconoscimento di queste stringhe è un problema computazionale simile all'addizione. Quindi, indipendentemente dalla lunghezza della stringa, il problema può essere risolto da un ASF sulla base dello stesso insieme di casi, rappresentati dai suoi stati. Questo si può capire guardando la finestra in figura 3, che contiene due parentesi. Se la finestra è posizionata all'inizio della stringa e spostata di due parentesi per volta, l'informazione contenuta nella finestra diviene sufficiente per giudicare se la stringa sia ben formata. Quando la finestra si sposta a un' altra coppia, tutta l'informazione circa la coppia precedente è irrilevante e può essere rimossa dalla memoria.
L'informazione contenuta in una finestra di lunghezza fissa è quindi sufficiente a riconoscere la stringa come ben formata. Dunque, ogni stringa di questa forma può essere riconosciuta da un ASF.
Il secondo tipo di stringa mostrato in figura 3 non può essere riconosciuto in questo modo, poiché consiste in una serie di parentesi annidate. In queste stringhe, la prima parentesi sulla sinistra è legata alla prima parentesi sulla destra, la seconda parentesi sulla sinistra alla seconda sulla destra e, in generale, l'n-esima parentesi sulla sinistra è relativa alla n-esima sulla destra. Qualsiasi finestra di larghezza predefinita non riuscirà, alla fine, a cogliere queste relazioni, poiché l'informazione contenuta in una finestra non è sufficiente per riconoscere stringhe arbitrarie di questo tipo come ben formate.
La differenza fondamentale tra le due serie di stringhe mostrate nella figura 3 risiede nella dipendenza che esiste tra le parentesi nelle stringhe. Nel primo caso si ha solo una dipendenza locale tra parentesi. Al contrario, nel secondo caso vi sono dipendenze non locali: per esempio, le parentesi più esterne sono correlate. Questa relazione non è locale, nel senso che la stringa di parentesi tra queste due può essere arbitrariamente lunga. A causa di queste dipendenze non locali, l'informazione sull'intera stringa deve essere disponibile durante tutto il processo di riconoscimento.
Le stringhe di parentesi sono in qualche modo analoghe al linguaggio, poiché entrambi sono composti da elementi costitutivi (le parentesi e le parole). Il linguaggio naturale è grammaticalmente confrontabile con le stringhe annidate mostrate in figura 3, poiché anche in quel caso si trovano dipendenze non locali (Wasow, 1989). Il riconoscimento della natura ben formata di una stringa di parentesi è dunque simile al processo di analisi di una frase a partire dai suoi elementi sintattici, ma è anche una forma di riconoscimento di pattern che illustra le relazioni più che casuali tra il riconoscimento del linguaggio e l'elaborazione visiva (Sereno, 1991).
A causa delle dipendenze non locali, le stringhe annidate del nostro esempio possono essere riconosciute, o prodotte, solo da dispositivi computazionali in cui vi sia una distinzione funzionale tra programma e memoria. In particolare, esse possono essere riconosciute, o prodotte, a causa delle interazioni tra il programma e la memoria in queste macchine. lllustrerò brevemente queste interazioni prendendo spunto dal processo di riconoscimento delle stringhe annidate della figura 3.
Il modello di memoria virtuale impiegato nella figura (fig. 4) consiste in un nastro come quello della macchina di Turing, sul quale viene immagazzinata la stringa di parentesi, una parentesi per ogni cella. Il programma consiste in un ASF che interagisce con la memoria. In primo luogo un sottoprogramma esplora il nastro (per esempio, da destra a sinistra) finché trova una combinazione di una parentesi aperta e una chiusa vicine. Si noti che questa è una dipendenza locale tra due parentesi, che può essere riconosciuta da un ASF. Nel caso di una stringa ben formata, quindi, questo sottoprogramma trova il centro della stringa. Se viene trovata questa combinazione di parentesi, viene iniziato un altro sottoprogramma che esplora il nastro con due finestre, ciascuna delle quali contiene una parentesi. Cominciando dal centro, questo programma verifica se la finestra a sinistra contiene una parentesi aperta e quella a destra contiene una parentesi chiusa. Se questo è il caso, il programma muove entrambe le finestre di una parentesi, a sinistra e a destra rispettivamente, e ripete la stessa procedura di verifica. L'intero processo viene ripetuto finché una delle finestre raggiunge l'estremità della stringa. Se le due estremità vengono raggiunte simultaneamente, la stringa è ben formata.
Si noti ciò che succede nel caso di una stringa ben formata come la seguente: "((()))". Dopo aver identificato il centro, il programma legge questa stringa nell'ordine: "()()()". Ma questa è una stringa del primo tipo presentato in figura 3; quindi, nell'interazione tra programma e memoria la stringa "((()))" viene trasformata in una stringa del primo tipo. Questa trasformazione è necessaria, poiché il programma è un automa che può riconoscere solo stringhe del primo tipo. Cioè, il programma può riconoscere solo dipendenze locali tra le parentesi. Ciononostante, il dispositivo computazionale nel suo complesso può riconoscere stringhe del secondo tipo presentato in figura 3, che sono computazionalmente più complesse di quelle del primo tipo poiché contengono dipendenze non locali tra le parentesi.
L'interazione tra programma e memoria, dunque, fa in modo che la complessità computazionale venga ridotta a un livello tale da poter essere elaborata da un ASF. In altre parole, la conoscenza contenuta in un automa viene usata per elaborare informazioni che non lo possono essere sulla base di quella sola conoscenza, cioè senza usare la memoria e ciò costituisce l'uso produttivo della conoscenza in un sistema computazionale.
L'uso produttivo della conoscenza nella cognizione è stato già illustrato con l'esempio del riconoscimento visivo degli oggetti basato sull'identificazione di una sintesi delle rappresentazioni dei singoli attributi visivi. Poiché un ASF è una forma di pianificazione esaustiva dei casi possibili, si può identificare una congiunzione di attributi con un ASF se quest'ultimo possiede una specifica rappresentazione sintetica. Quindi, l'identificazione delle rappresentazioni sintetiche è basata su un'esplosione combinatoriale di rappresentazioni. Come abbiamo chiarito in precedenza, la conoscenza incorporata in un automa sotto forma di rappresentazioni può essere usata in modo più produttivo se esso interagisce con una memoria di lavoro funzionalmente distinta. In questo modo, nel caso del riconoscimento visivo di oggetti, si possono usare automi di questo genere per immagazzinare le rappresentazioni dei singoli attributi. L'interazione con una memoria di lavoro permette a questi automi di essere usati per elaborare le sintesi degli attributi. Prima di descrivere questa procedura in maggior dettaglio, fornirò una descrizione diversa, ma equivalente, della memoria di lavoro nei dispositivi computazionali esemplificati in figura 4, in grado di rendere più facile l'identificazione di potenziali memorie di lavoro nelle strutture neuronali trovate nel cervello.
La memoria di lavoro come spazio delle configurazioni
La memoria di lavoro che abbiamo appena descritto (v. figura 4) può essere raffigurata in forma diversa, ma funzionalmente equivalente (fig. 5). In questo caso ogni cella (posizione) sul nastro consta di due sottocelle: quella in alto rappresenta la parentesi aperta e quella in basso la parentesi chiusa. Ogni sottocella è così una rappresentazione di una parentesi, che viene immagazzinata su una posizione del nastro attivando la sua sottocella (ovvero, la sua rappresentazione) in quella posizione. Le parentesi rosse in figura 5 sono le rappresentazioni attivate. Una particolare stringa di parentesi immagazzinate sul nastro è quindi una particolare configurazione di sottocelle attivate. Diverse configurazioni possono essere attivate sullo stesso nastro, come risulta dalla figura 5. L'insieme totale delle configurazioni che possono essere attivate su un nastro costituisce lo spazio delle configurazioni di quel nastro. Dunque, invece di considerare un nastro (o una qualsiasi memoria di lavoro) come una struttura nella quale vengano immagazzinate configurazioni di simboli (cioè, le rappresentazioni), lo si può considerare come una struttura nella quale vengano attivate configurazioni di rappresentazioni (cioè, i simboli).
La produttività computazionale del dispositivo illustrato in figura 4 deriva dalle interazioni tra il suo spazio delle configurazioni e le strutture che rappresentano la conoscenza in questo dispositivo, ovvero gli automi a stati [miti del suo programma. In altre parole, un processo computazionale in un dispositivo del genere consiste nelle interazioni tra le rappresentazioni in uno spazio di configurazioni e le rappresentazioni in strutture di conoscenza (van der Velde, 1996; 1997).
Lo spazio delle configurazioni per l'elaborazione visiva
La comprensione di una scena visiva complessa può derivare dall'uso produttivo della conoscenza rappresentazionale solo se vi è uno spazio delle configurazioni per l' elaborazione visiva. La figura (fig. 6) fornisce un esempio astratto di un simile spazio, basato su due caratteristiche elementari degli oggetti presenti in ogni posizione del campo visivo, cioè se essi contengono linee verticali o orizzontali. Dunque, una configurazione in questo spazio consiste in una distribuzione di quadrati e di rettangoli. Due di questi sono mostrati in figura 6. Si noti che tali configurazioni sono diverse e nello stesso tempo si somigliano, perché sono composizioni degli stessi oggetti in posizioni (assolute e relative) diverse. Un dispositivo computazionale produttivo non elaborerebbe la distribuzione mostrata in figura 6 sulla base delle rappresentazioni possedute per ogni configurazione. Esso possiederebbe piuttosto rappresentazioni di identità (invarianti rispetto alla posizione) dei singoli oggetti. Una particolare disposizione degli oggetti verrebbe rappresentata temporaneamente nello spazio delle configurazioni illustrato in figura 6. L'analisi di questa composizione deriverebbe dalle interazioni tra lo spazio delle configurazioni e le rappresentazioni di identità. Poiché esse differiscono per le posizioni relative e assolute degli oggetti, la comprensione di queste immagini consisterebbe, in particolare, nel mettere in relazione l'identità degli oggetti con la loro posizione. Consisterebbe quindi in una soluzione del binding problem, che abbiamo già discusso, tra la rappresentazione dell'identità e della posizione. Si può in effetti fornire una soluzione a questo problema nei termini dell'interazione tra lo spazio delle configurazioni e le rappresentazioni di identità e si può usare questa soluzione, per esempio, per formulare modelli formali dei risultati ottenuti da L. Chelazzi e collaboratori (1993) sulla ricerca visiva. Illustrerò l'interazione tra uno spazio delle configurazioni e le rappresentazioni di identità attraverso una breve descrizione di questo modello.
La sintesi tra rappresentazioni di posizione e identità nella elaborazione visiva
Nell'esperimento di Chelazzi e collaboratori venivano mostrati due oggetti (per esempio, un triangolo e un quadrato) e l'animale doveva focalizzare la sua attenzione su uno di essi, che era precedentemente presentato come lo stimolo target (per esempio, il triangolo). Il compito consisteva quindi nell'identificare nel campo visivo la posizione di un oggetto dato, in presenza del distrattore. I risultati hanno dimostrato che in un primo tempo entrambi gli oggetti attivavano la loro rappresentazione di identità, invariante rispetto alla posizione. In seguito, la rappresentazione dello stimolo target rimaneva attiva, mentre quella del distrattore si indeboliva. Un po' di tempo dopo questo indebolimento, l'animale compiva un movimento oculare saccadico verso la posizione dello stimolo target.
Questo esperimento mostra che la posizione dello stimolo target veniva trovata dopo che la sua rappresentazione di identità era stata selezionata come la sola rappresentazione attiva. Questo fatto suggerisce che la rappresentazione di identità attiva innescasse la selezione della rappresentazione della posizione dello stimolo target. D'altra parte, la rappresentazione di identità dello stimolo target è invariante rispetto alla posizione e non può quindi di per sé fornire informazioni sulla posizione dello stimolo stesso. Si può però trovare questa posizione sulla base della interazione tra la rappresentazione di identità e uno spazio delle configurazioni. La figura (fig. 7) descrive sommariamente questa interazione (van der Velde, 1997). Nello schema presentato in figura, la scena viene prima analizzata in uno spazio delle configurazioni, che consiste in rappresentazioni di caratteristiche elementari in ogni posizione del campo visivo. Ogni oggetto sulla scena attiva le rappresentazioni specifiche rispetto alla posizione delle sue caratteristiche in questo spazio. Ogni scena attiva quindi una configurazione in questo spazio.
Lo spazio delle configurazioni è connesso in cascata (v. figura 7, in alto) alle rappresentazioni di identità, che sono invarianti rispetto alla posizione, e alle rappresentazioni della posizione, che non codificano l'identità. Le rappresentazioni attive delle caratteristiche nello spazio delle configurazioni attivano la rappresentazione di identità dell'oggetto al quale appartengono. Questo si può ottenere con una rete neuronale artificiale di tipo feedforward (con propagazione in avanti) che connette lo spazio delle configurazioni alle rappresentazioni di identità (Wallis e Rolls, 1996). In generale, una rete neuronale consiste di nodi (o neuroni) e connessioni. I nodi inviano e ricevono degli impulsi di attivazione attraverso le connessioni che li legano agli altri nodi della rete; perciò, è chiaro che solo i nodi che sono in contatto fra loro potranno attivarsi l'un l'altro. Una rete a regolazione anticipativa è una rete composta di strati separati di nodi disposti in modo gerarchico: uno strato inferiore, uno superiore e un certo numero di strati intermedi. Le connessioni fra gli strati sono organizzate in modo tale che l'attivazione possa viaggiare solo da uno strato inferiore verso uno superiore (da qui la definizione di regolazione anticipativa).
L'attività locale delle caratteristiche nello spazio delle configurazioni può anche dar luogo all'attivazione delle due rappresentazioni di posizione che corrispondono alla posizione degli oggetti nella scena. Con due oggetti, quindi, vengono attivate inizialmente due rappresentazioni di identità e due rappresentazioni di posizione, che costituiscono il binding problem tra l'identità e la posizione. Questo problema viene risolto se, dopo aver selezionato una rappresentazione di identità, si riesce a trovare la corretta rappresentazione della posizione.
L'esperimento di Chelazzi e collaboratori mostra che una selezione della rappresentazione di identità ha in effetti luogo. Di conseguenza, la rappresentazione di identità dello stimolo target rimane la sola rappresentazione attiva. Essa quindi, come suggeriscono i risultati dell'esperimento, innesca la selezione della posizione dello stimolo. Nel modello illustrato in figura 7, questa attivazione selettiva deriva da un'interazione tra le rappresentazioni di identità e quelle di caratteristiche all'interno dello spazio delle configurazioni.
Questa interazione viene prodotta da microcircuiti locali nello spazio delle configurazioni, che vengono attivati da due sorgenti: dalle rappresentazioni locali di caratteristiche attive nello spazio delle configurazioni e dalle rappresentazioni di identità attive che corrispondono a queste caratteristiche. Quest'ultima sorgente di attivazione deriva dalle connessioni retro attive tra le rappresentazioni di identità e le corrispondenti rappresentazioni delle caratteristiche nello spazio delle configurazioni. Queste connessioni sono speculari alle connessioni feedforward che producono l'attivazione delle rappresentazioni di identità (v. figura 7, in basso). Dopo la selezione della rappresentazione dello stimolo target come la sola rappresentazione di identità attiva, le due condizioni di attivazione sono soddisfatte solo per i microcircuiti che codificano la posizione dello stimolo target nello spazio delle configurazioni. La posizione corretta può dunque essere recuperata. L'attivazione dei microcircuiti che codificano questa posizione può essere usata per selezionare la rappresentazione della posizione che corrisponde alla posizione dello stimolo target. Quindi, come risultato di questa selezione, si può generare la risposta.
È importante capire che in questo modello la posizione dello stimolo target si può recuperare solo grazie all'interazione tra lo spazio delle configurazioni e la rappresentazione di identità dello stimolo. Le caratteristiche attive nello spazio delle configurazioni rappresentano di per sé l'informazione sulla sua posizione, ma non un'informazione sufficiente sulla sua identità, mentre la rappresentazione di identità attiva non fornisce di per sé l'informazione sulla posizione.
Si può considerare il processo che abbiamo descritto come una forma di attenzione selettiva, in cui l'identità di un oggetto innesca la selezione di altri attributi dell'oggetto stesso, in questo caso la sua posizione. Analogamente potrebbero essere selezionate altre caratteristiche, come il colore. Il modello può quindi essere applicato per risolvere il binding problem a proposito di forma e colore (van der Velde, 1996). Inoltre, l'interazione tra lo spazio delle configurazioni e le rappresentazioni di identità che abbiamo descritto può anche procedere in senso inverso. In questo modo si può usare una rappresentazione di posizione prescelta per selezionare la rappresentazione di identità dell'oggetto in quella posizione, il che equivale a simulare il processo di attenzione spaziale selettiva.
Aspetti cognitivi dell'apprendimento incrementale
Il modello che abbiamo descritto illustra il modo in cui si può evitare l'esplosione combinatoriale delle rappresentazioni, tipica di un modello basato su ASF. Come si è detto, la produttività computazionale di modelli di questo tipo dipende dall'interazione tra due tipi di rappresentazioni: nello spazio delle configurazioni e di identità. Grazie alle interazioni tra queste rappresentazioni, si può usare una quantità limitata di conoscenza per elaborare una quantità illimitata di informazione.
Le rappresentazioni nello spazio delle configurazioni costituiscono le informazioni here and now (hic et nunc, cioè di impiego immediato) necessarie per la soluzione di un particolare problema, per esempio la scena che deve essere identificata. Le rappresentazioni di identità, d'altra parte, costituiscono la conoscenza permanente che il sistema deve possedere per risolvere il problema. Questa conoscenza è permanente nel senso che non cambia così velocemente come quella immediata nello spazio delle configurazioni. In un sistema cognitivo naturale, questa conoscenza permanente viene acquisita gradualmente nel tempo attraverso l'interazione con l'ambiente. Essa è cioè il risultato di un apprendimento incrementale (o sequenziale) che avviene quando il materiale da apprendere si presenta un po' alla volta, come nel caso dell'accrescimento graduale nel proprio vocabolario di una lingua straniera. Il punto cruciale è che, quando si imparano parole nuove, non è necessario ripassare quelle vecchie. Cioè, la memorizzazione di parole nuove non interferisce con la memorizzazione di parole già familiari.
L'apprendimento incrementale è la modalità caratteristica in cui avviene l'apprendimento. In questo modo, attraverso l'esperienza o attraverso l'insegnamento, la conoscenza può aumentare senza eliminare le conoscenze già acquisite. Nell'elaborazione visiva, per esempio, un animale può imparare nel tempo a riconoscere nuove forme visive (Miyashita, 1988) secondo un processo come quello rappresentato in figura 7. In questo modello si assume che l'identificazione (il riconoscimento) di un oggetto in una scena sia prodotta da una rete feedforward (v. figura 7, in alto). La rete usa le rappresentazioni delle caratteristiche attive, prodotte dall'oggetto nello spazio delle configurazioni, per dar luogo a un insieme di neuroni attivi che rappresentano l'identità dell'oggetto (per esempio, la sua forma). In altre parole la rete produce una funzione i cui input sono le rappresentazioni delle caratteristiche e il cui output è la rappresentazione dell'identità.
Si è dimostrato in modo formale che le reti feedforward con più di due strati possono produrre funzioni di tipo molto generale (Hornik et al., 1989) e si è anche dimostrato che tali reti possono apprendere funzioni, cioè si possono presentare alla rete coppie input-output della funzione e si possono modificare i pesi (v. i saggi di J. Cowan, Storia dei concetti e delle tecniche nella ricerca sulle reti neurali, e di M. Opper, Imparare a generalizzare) delle connessioni sulla base di una regola (Rumelhart et al., 1986). Dopo un certo numero di sessioni di addestramento, la rete produrrà l'output desiderato per un dato input. Quindi, nei termini del modello mostrato in figura 7, la rete può imparare nel tempo nuove associazioni.
La scoperta del fatto che le reti con architettura multi strato di tipo feedforward possono produrre e imparare funzioni è stata in effetti uno dei motivi principali dell'ascesa (o del risveglio) del connessionismo negli anni Ottanta. Da allora però molti ricercatori hanno evidenziato una seria difficoltà presente nell' apprendimento di funzioni da parte di queste reti, riguardante il fatto che, in tali modelli, l'apprendimento di nuove informazioni cancella le vecchie, secondo un fenomeno definito interferenza distruttiva o catastrofica.
L'interferenza distruttiva nelle reti feedforward
La interferenza distruttiva nelle reti è stata studiata, per esempio, da M. McCloskey e N.J. Cohen (1989) e da R. Ratcliff (1990). Questi autori hanno addestrato una rete a riconoscere un insieme di associazioni stimolo-risposta o, in termini di funzioni, un insieme di coppie input-output. La rete è stata quindi addestrata a riconoscere un secondo insieme di coppie input-output, diverse da quelle presentate durante la prima fase di addestramento; dopo di che si sono osservate le prestazioni sul primo insieme. l risultati hanno mostrato che il riconoscimento del primo insieme di stimoli era stato perso e poteva essere preservato solo se questo insieme veniva ripresentato alla rete durante l' apprendimento del secondo. La prestazione ottimale, cioè, viene preservata solo se entrambi gli insiemi sono combinati in un solo insieme, e la rete viene addestrata a riconoscere questo insieme in una volta sola.
Questo comportamento delle reti feedforward si può spiegare informalmente in base al teorema di K. Hornik e dei suoi collaboratori. Questi autori (Hornik et al., 1989) hanno dimostrato che le reti feedforward possono approssimare una classe molto generale di funzioni matematiche che operano su domini di input ristretti. Per esempio, una rete feedforward come quella mostrata in figura (fig. 8) può approssimare qualsiasi funzione continua di una variabile reale su un intervallo ristretto, cioè limitato e chiuso, dell'asse reale. Questo vuoI dire che esiste un insieme di pesi delle connessioni tale che la rete produce la funzione desiderata per qualsiasi input che appartiene a questo intervallo.
Il punto cruciale di questo teorema è il fatto che l' approssimazione è corretta solo su un intervallo ristretto. Questo implica che l'insieme dei pesi delle connessioni dipende non solo dalla funzione da approssimare, ma anche dal dominio di input sul quale l'approssimazione vale. La figura 8 illustra questo punto. Supponiamo che la rete abbia imparato ad approssimare la curva verde sull'intervallo indicato a sinistra. Oltre alla curva verde, però, vi sono molte altre funzioni che assumono gli stessi valori su questo intervallo, ma con valori diversi al di fuori, come nel caso della curva rossa. È ovvio che anche queste funzioni sono approssimate dalla rete su questo intervallo, usando lo stesso insieme di pesi delle connessioni. In effetti, la rete non può distinguere una qualsiasi di queste funzioni dalle altre. Fuori dall'intervallo, però, le funzioni sono diverse. Si ha quindi una probabilità nulla che la rete approssimi la curva verde al di fuori dell'intervallo, usando lo stesso insieme di pesi delle connessioni. Si deve dunque cambiare tale insieme per approssimare la curva verde al di fuori dell'intervallo dato. Per esempio, verrà generato un nuovo insieme di pesi delle connessioni, se la rete viene addestrata ad approssimare la curva verde sull'intervallo a destra in figura. Sulla base dello stesso ragionamento di cui sopra, però, questo insieme di pesi delle connessioni non consentirà alla rete di approssimare la curva verde al di fuori del nuovo intervallo. In particolare, la rete non approssimerà più la curva verde nell'intervallo a sinistra nella figura. Dunque, la conoscenza acquisita nella prima sessione di addestramento è persa. Questa è una conseguenza del fatto che le approssimazioni sull'intervallo sinistro e destro sono apprese in sequenza. La rete approssimerà la curva verde su entrambi gli intervalli solo se questo comportamento su entrambi gli intervalli viene appreso allo stesso tempo.
Apprendimento incrementale negli automi a stati finiti
Il comportamento delle reti feedforward che abbiamo descritto è caratteristico dell'apprendimento negli ASF. Una funzione, o un comportamento, prodotta da un automa deriva dalle transizioni tra i suoi stati interni. L'apprendimento quindi consiste nel modificare queste transizioni, per esempio aggiungendo a esso nuovi stati. A causa di queste modifiche, la struttura computazionale della macchina cambierà e dunque cambierà il comportamento da essa prodotto. In altre parole, l'apprendimento incrementale, di importanza vitale per produrre un comportamento cognitivo (intelligente), non è possibile nell'ambito di un solo ASF. La soluzione a questo apparente dilemma sembra ovvia. Non si dovrebbe imparare un'intera funzione (o uno schema di comportamento) con un solo ASF, per esempio una sola rete. La funzione dovrebbe invece essere suddivisa in sottoinsiemi imparati da reti diverse.
Un esempio di questa soluzione si trova nella corteccia visiva dei primati. La via anatomo-funzionale deputata al riconoscimento visivo termina nella corteccia infero-temporale. In quest'area si sono trovate colonne di cellule che rispondono selettivamente a un insieme di caratteristiche visive simili e moderatamente complesse (Tanaka, 1996). Ognuna di queste colonne sarà probabilmente lo stato terminale di una rete feedforward particolare e specializzata. Dopo che è avvenuto l'apprendimento, i pesi delle connessioni di questa rete produrranno l'attivazione selettiva osservata delle cellule della colonna. Poiché ogni colonna risponde solo a un insieme di caratteristiche visive simili, in queste reti non si avrà interferenza distruttiva. Tuttavia qui sorge un problema che ci è familiare. Secondo K. Tanaka (1996): "Poiché [...] le cellule all'interno di una singola colonna rispondono a caratteristiche simili, la computazione effettuata all'interno di una colonna può fornire informazioni solo su caratteristiche parziali (globali o locali) delle immagini degli oggetti. Per rappresentare l'intera immagine di un oggetto si devono combinare le computazioni che hanno luogo in molte colonne diverse, o molte decine. Questo fatto evoca il binding problem, cioè come discriminare differenti insiemi di attività quando vi sono [due o più] oggetti in posizioni retiniche vicine". Dunque l'apprendimento incrementale da parte di un ASF porta a una suddivisione della conoscenza acquisita. Durante l'elaborazione dell'informazione, questa conoscenza suddivisa, rappresentata in automi diversi, si deve temporaneamente ricombinare. Questo processo di ricombinazione richiede l'interazione tra questi automi e gli spazi delle configurazioni, come abbiamo già discusso.
Conclusioni
Per comprendere in che modo il cervello produce un comportamento intelligente, si devono sviluppare modelli che mettano in relazione i processi di attivazione nelle strutture neuronali con il comportamento osservabile. Nel caso del comportamento intelligente, però, è difficile mettere in relazione direttamente il comportamento con i processi neuronali sottesi. Sarà invece necessario un approccio più indiretto, in cui vengano integrate informazioni provenienti dalle neuroscienze e dalla psicologia sulla base di modelli computazionali.
Questi modelli dovranno essere formulati nei termini dei processi di attivazione nelle strutture neuronali studiati dalle neuroscienze. Essi però dovranno anche soddisfare i requisiti computazionali necessari per produrre il comportamento cognitivo studiato in psicologia. In altre parole, lo studio dei modelli computazionali necessari per produrre un comportamento intelligente deve essere integrato con lo studio delle strutture neuronali che possono realizzare questi modelli. Una caratteristica dei modelli computazionali, di particolare importanza per la produzione di un processo cognitivo, riguarda la distinzione funzionale tra le strutture in cui viene immagazzinata temporaneamente l'informazione e quelle in cui è immagazzinata la conoscenza del sistema. La produzione di un processo cognitivo risulta dall'interazione tra queste strutture, poiché tale distinzione consente l'uso produttivo della conoscenza già acquisita nell'elaborare informazione nuova e l'apprendimento incrementale di conoscenze nuove.
Sia l'uso produttivo della conoscenza acquisita sia la capacità di acquisirne nel tempo sono necessari per interagire con l'ambiente in modo intelligente. Perciò, la comprensione del modo in cui il cervello produce un comportamento intelligente dipende dalla comprensione del modo in cui questi processi sono realizzati nel cervello.
Bibliografia citata
AMSEL, A., RASHOTTE, M.E., a c. di (1984) Mechanisms of adaptive behavior: Clark L. Hull's theoretical papers, with commentary. New York, Columbia University Press.
CHELAZZI, L., MILLER, E.K., DUNcAN, J., DESIMONE, R. (1993) A neural basis for visual search in inferior temporal cortex. Nature, 363, 345-347.
DOUGLAS, R.J., MARTIN, K.A.C., WHITTERIDGE, D. (1989) A canonical microcircuit for neocortex. Neural Comput., l, 480-488.
DOWLING, J.E. (1992) Neurons and networks: an introduction to neuroscience. Cambridge, Mass., Belknap Press of Harvard University Press.
FODOR, J.A., PYLYSHYN, Z.W. (1988) Connectionism and cognitive architecture: a criticaI analysis. In Connections and symbols, a C. di Pinker S., Mehler J., Cambridge, Mass., MIT Press.
GAZZANIGA, M.S. (1995) Preface. In The cognitive neurosciences, a c. di Gazzaniga M.S., Cambridge, Mass., MIT Press.
HEBB, D.O. (1949) The organization of behavior: a neuropsychological theory. New York, Wiley.
HEILIGENBERG, W. (1991) Neural nets in electric fish. Cambridge, Mass., MIT Press.
HORNIK, K., STINCHCOMBE, M., WHITE, H. (1989) Multilayer feedforward networks are universal approximators. Neural Networks, 2, 359-366.
KOSSLYN, S.M., SHIN, L.M. (1992) The status of cognitive neuroscience. Curr. Opin. Neurobiol., 2, 146-149.
McCLOSKEY, M., COHEN, N.I. (1989) Catastrophic interference in connectionist networks: the sequential leaming problem. In The psychology of learning and motivation, a c. di Bower G.H., San Diego, Academic Press.
McLEOD, C.M. (1991) Half a century of research on the Stroop effect: an integrative review. Psychol. Bull., 109, 163-203.
MARTIN, K.A.C. (1994) A brief history of the 'feature detector'. Cereb. Cortex, 4, 1-7.
MATURANA, H.R., LETTVIN, J.R., McCULLOCH, W.R., PITTS, W.H. (1960) Anatomy and physiology of vision in the frog (Rana pipiens). J. Gen. Physiol., 43, 129-171.
MINSKY, M.L., (1967) Computation: finite and infinite machines. Englewood Cliffs, Prentice Hall.
MISNER, C.W., THORNE, K.S., WHEELER, J.A. (1973) Gravitation. San Francisco, Freeman.
MIYASHITA, Y. (1988) Inferior temporal cortex: where visual perception meets memory. In Annu. rev. neurosci., voI. 16, a c. di Cowan W.M., Palo Alto, Annual Reviews Inc.
NEUMANN, J. VON (1988) The computer and the brain. In Neurocomputing: Joundations of research, 2 voll. 1988-1990, a c. di Anderson J.A., Rosenfeld E., Cambridge, Mass., MIT Press.
NEWELL, A. (1980) Physical symbol systems. Cognitive Science, 4, 135-183.
NEWELL, A. (1990) Unified theories of cognition. Cambridge, Mass., Harvard University Press.
POSNER, M.I., RAICHLE, M.E. (1994) Images of mind. New York, Freeman.
RATCLIFF, R. (1990) Connectionist models ofrecognition memory: constraints imposed by learning and forgetting functions. Psychol. Rev., 97, 285-308.
RUMELHART, D.E., HINTON, G.E., WILLIAMS, R.I. (1986) Learning and internaI representations by error propagation. In voI. I di Parallel distributed processing: explorations in the microstructure of cognition, 2 volI., a c. di Rumelhart D.E., McClelland J.L., Cambridge, Mass., MIT Press.
SERENO, M.I. (1991) Language and the primate brain. Proceedings of the 13th Annual ConJerence of the Cognitive Science Society. Hillsdale, Erlbaum Associates.
TANAKA, K. (1996) Representation ofvisual features of objects in the inferotemporal cortex. Neural Networks, 9, 1459-1475.
TREISMAN, A. (1996) The binding problem. Curr. Opin. Neurobiol., 6, 171-178.
VELDE, F. VAN DER (1996) Integrating connectionism and symbol manipulation, submitted.
VELDE, F. VAN DER (1997) On the use of computation inmodelling behavior. Network: Computation in Neural Systems, 8, in press.
W ALLIS, G., ROLLS, B.T. (1996) Invariant face and object recognition in the visual system. Progr. Neurobiol., in presso WASOW, T. (1989) Grammatical theory. In Foundations of cognitive science, a c. di Posner M.I., Cambridge, Mass., MIT Press.
Bibliografia generale
ARBIB, M.A., a c. di, The handbook of brain theory and neural networks. Cambridge, Mass., MIT Press, 1995.
GAZZANIGA, M.S., a c. di, The cognitive neurosciences. Cambridge, Mass., MIT Press, 1995.
KOCH, C., DA VIS, J.L., a C. di, Large-scale neuronal theories of the brain. Cambridge, Mass., MIT Press, 1994.
KOSSLYN, S.M., ANDERSEN, R.A., a c. di, Frontiers in cognitive neuroscience. Cambridge, Mass., MIT Press, 1992.
POSNER, M.I., a c. di, Foundations of cognitive science. Cambridge, Mass., MIT Press, 1989.
SHEPHERD, G.M., a C. di, The synaptic organization of the brain, 3a ed., Oxford, Oxford University Press, 1990.