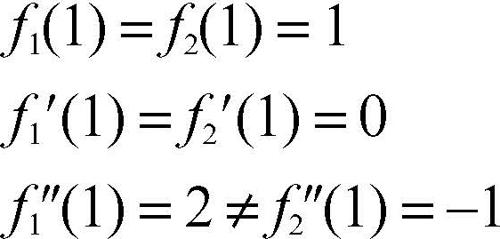contatto tra due curve

contatto tra due curve

contatto tra due curve punto in cui due curve si intersecano e hanno almeno una retta tangente in comune. In generale, si dice che due curve hanno nel punto P un contatto di ordine k quando nel punto in cui le due curve si incontrano cadono n + 1 punti di intersezione infinitamente vicini; ciò equivale a dire che le funzioni che le rappresentano e le loro derivate fino all’ordine k, calcolate nel punto P, coincidono, mentre le derivate di ordine k + 1, calcolate nel punto P, assumono valori differenti. Per esempio, le parabole di equazioni

hanno, nel punto P(1, 1) un contatto di ordine 1, detto anche contatto bipunto, in quanto risulta:

Nel punto P cadono due punti di intersezione infinitamente vicini, che, per così dire, sono “assorbiti” in un solo punto. Se infatti, mantenendo il passaggio di ciascuna delle due parabole per P, le si “muovono di poco”, esse si intersecano in due punti distinti. Riportando con continuità le due parabole alla posizione iniziale di tangenza, i due punti si sovrappongono nell’unico punto di contatto. Con analoghe considerazioni, di carattere prevalentemente intuitivo, si può affermare che se in P c’è un contatto tra due curve di ordine 2, 3, ... k si ha, rispettivamente, un contatto tripunto, quadripunto, ..., (k + 1)-punto. Se intersecandosi, due curve hanno in un punto contatto di ordine k, tale punto viene contato con molteplicità di intersezione k + 1. Quando l’ordine del contatto k è dispari le due curve nel punto di contatto non si attraversano; se invece l’ordine è pari, le due curve, pur toccandosi nel punto di contatto, si attraversano. Anche per due superfici si parla di contatto in un punto in comune quando in quel punto hanno il piano tangente in comune.