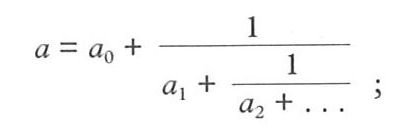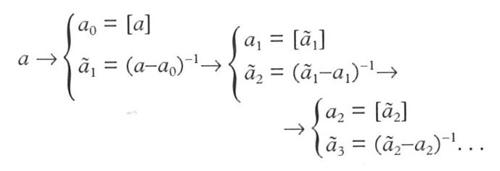continuo 1

continuo 1

contìnuo¹ [agg. Der. del lat. continuus, da continere "tenere unito", comp. di cum "insieme" e tenere, e quindi "non interrotto"] [ALG] Applicazione c.: applicazione definita su uno spazio topologico A a valori in un altro spazio topologico A' che fa corrispondere a punti "vicini" di A punti "vicini" di A'; precis., se al punto P di A corrisponde il punto P' di A', fissato un intorno qualunque I' di P', esiste un intorno I di P che viene trasformato in un aperto di A' tutto contenuto in I'. Costituisce una generalizzazione del concetto di funzione c. (v. oltre). ◆ [ALG] Frazione c.: rappresentazione dei numeri positivi a mezzo di successioni di interi. Se a è un intero positivo, allora a può essere scritto in uno e un solo modo come:

indicando con [x] la parte intera di x, la successione ai si costruisce con il seguente algoritmo:

Il numero a è razionale se e solo se per un certo j si ha aj=∞, ossia la frazione c. si tronca. La frazione c. si denota di solito con il simbolo [a₀; a₁; a₂; ...].

◆ [ANM] Funzione c.: una funzione f(x) di variabile reale a valore reale è tale in un punto x₀ se lim_x®x0 f(x)=f(x₀), ossia se per ogni e>0 si può trovare un d>0 tale che se |x-x₀|<d allora |f(x)-f(x₀)|<e. Una funzione c. in tutti i punti di un intervallo si dice c. su quell’intervallo. Quando una funzione c. in un intervallo è tale che per ogni e>0 esiste un d>0 tale che se |x-x₀|<d allora |f(x)-f(x₀)|<e e il d non dipende dal punto x₀ dell’intervallo la funzione è detta uniformemente c. su quell’intervallo; per le funzioni equiuniformemente c. →equicontinuo. Le nozioni di continuità e di uniforme continuità si generalizzano in modo ovvio alle funzioni definite su spazi più generali. ◆ [ALG] Gruppo c.: gruppo i cui elementi dipendono da parametri arbitrari (o da funzioni arbitrarie) variabili con continuità, in modo che da un elemento qualunque del gruppo si possa passare a ogni altro usufruendo di tale variazione continua. ◆ [ALG] Insieme c.: ogni insieme coincidente con l’insieme dei suoi punti limite. qn Processo c. in probabilità e in media di ordine p: v. processi stocastici: IV 607 c. ◆ [ALG] Sistema c. di varietà algebriche: insieme di varietà sopra una varietà ambiente dipendenti da certi parametri variabili con continuità; per es., l’insieme delle generatrici di una rigata. ◆ [MCC] Sistema materiale c.: generico sistema deformabile, senza ulteriori precisazioni circa la sua natura: per es., sia un blocco o un filo d’acciaio, sia un liquido o un gas: v. meccanica dei continui.