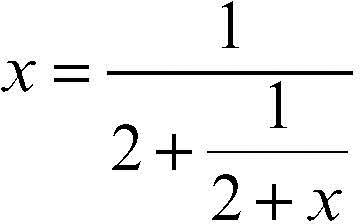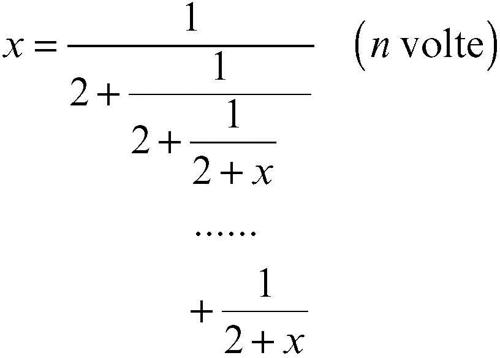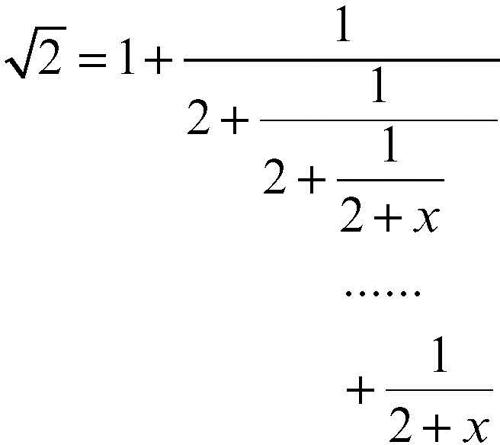algoritmo, convergenza di un

algoritmo, convergenza di un

algoritmo, convergenza di un espressione che, in un algoritmo iterativo, indica la possibilità di giungere a un risultato in un numero finito di passi, o attraverso l’individuazione del risultato vero o attraverso una sua approssimazione attendibile. Un algoritmo di calcolo è, nella gran parte dei casi, caratterizzato dalla ripetizione (iterazione) di una o più operazioni: ripetizione controllata da un criterio che ne consente l’interruzione dopo un numero stabilito di volte o comunque al verificarsi di una data condizione. In particolare, un algoritmo contiene spesso un ciclo di istruzioni la cui esecuzione viene re-iterata più volte e a ogni successiva iterazione si ottengono nuovi valori delle variabili fino ad avere il valore desiderato. Un algoritmo di questo tipo è detto algoritmo iterativo; l’utilizzo di algoritmi iterativi è particolarmente significativo quando si vuole calcolare approssimativamente il valore di un’espressione che non è possibile determinare con esattezza. Per esempio, poiché non è possibile esprimere in forma decimale il valore esatto di π, si calcolano alcune sue buone approssimazioni con un metodo iterativo, costruendo così una successione di sue approssimazioni. Deve trattarsi di un metodo iterativo convergente, cioè tale da fornire valori che successivamente tendano a un valore finito. All’aumentare del numero di iterazioni eseguite diminuisce la differenza tra il valore esatto di π e il valore approssimato via via ottenuto. Se quindi per calcolare il valore v di un’espressione si utilizza un algoritmo iterativo, si ottiene a ogni successiva iterazione un nuovo valore v_i. La successione di valori così ottenuta può, dopo un certo numero di iterazioni, fornire il valore esatto di v oppure può continuare a fornire le sue approssimazioni, ma con un errore sempre minore. In questo secondo caso i valori numerici che si ottengono sono i primi termini di una successione {v_i}, teoricamente infinita, convergente (→ successione, convergenza di una) e il valore esatto di v è il valore limite a cui essa converge. Poiché un algoritmo è necessariamente finito, si otterranno soltanto delle approssimazioni di v, ma, aumentando il numero di iterazioni eseguite, si tratterà di approssimazioni sempre più precise. In entrambi i casi – sia che si giunga al valore esatto, sia che si giunga a una sua approssimazione con la precisione voluta – l’algoritmo è iterativo e convergente.

Si calcoli, per esempio, con un particolare metodo iterativo convergente il valore del numero irrazionale √(2), a partire dal fatto che il numero x {{{1}}}√(2) − 1 è una delle soluzioni dell’equazione di secondo grado x² + 2x − 1 = 0 (l’altra soluzione è il numero −√(2) − 1). Riscrivendo (per x ≠ −2) l’equazione nella forma

si osserva che a destra compare di nuovo x e sostituendo a essa il valore

si ottiene

Ripetendo l’operazione n volte si ha

Poiché x {{{1}}}√(2) − 1 si ha: √(2) = x − 1; sostituendo nell’espressione precedente si ottiene

All’aumentare del numero n di iterazioni il valore di √(2) è approssimato da 1 + x. Su questa base si può costruire un algoritmo iterativo per calcolare valori approssimati di √(2).

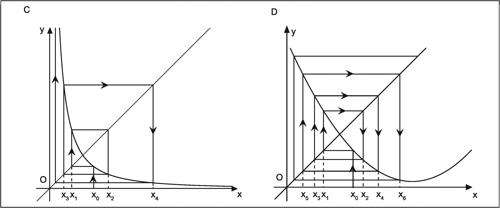
L’esempio si presta a una generalizzazione per la ricerca di ciascuna delle soluzioni di un’equazione scritta nella forma x = ƒ(x) dove ƒ: R → R è una funzione continua. Si può infatti costruire una successione di approssimazioni della soluzione {x_i} dove x_n+1 = ƒ(x_n): se tale successione è convergente, allora il valore cui essa converge è una soluzione dell’equazione. Pertanto, se è possibile costruire una successione {x_i} con x_n+1 = ƒ(x_n) che sia convergente, allora è possibile costruire un algoritmo iterativo convergente per il calcolo approssimato della soluzione dell’equazione x = ƒ(x). Poiché quest’ultima rappresenta graficamente i punti di intersezione tra la funzione y = ƒ(x) e la retta y = x, si possono presentare diverse situazioni.

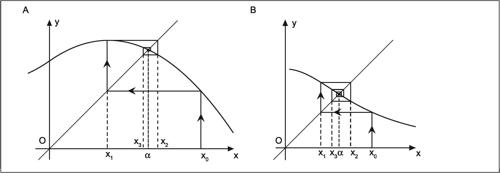
Nei grafici

, la successione converge al valore α: in questo caso si ha la convergenza della soluzione approssimata, che ne indica anche la stabilità.

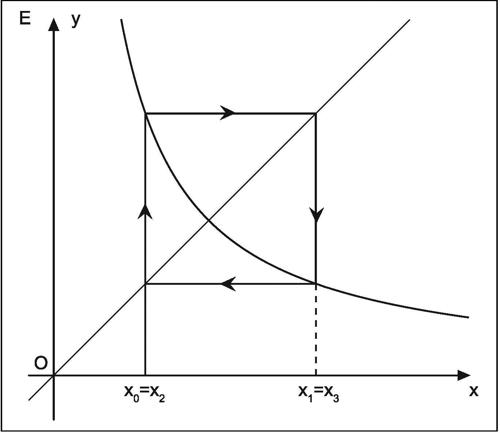
, invece, la successione non è convergente, poiché i valori si allontanano sempre più dal punto di intersezione. Infine,

la successione non converge né diverge, ma oscilla continuamente tra due valori.

Nel metodo iterativo convergente la ricerca di una soluzione approssimata di un’equazione si può arrestare attraverso il controllo dell’errore commesso approssimando la soluzione dell’equazione con il valore ottenuto all’n-esimo passo x_n. Se si vuole ottenere un risultato con un errore di ordine di grandezza minore di 10^−k, occorre arrestare il calcolo quando la differenza tra due successivi valori ottenuti è minore di 10^−k:

A seconda del metodo iterativo utilizzato, la convergenza avviene più o meno velocemente. Per esempio, per la determinazione di uno zero reale di una funzione ƒ(x), cioè una soluzione dell’equazione ƒ(x) = 0, si possono utilizzare metodi con diverse caratteristiche sia per quanto riguarda il numero di passi del calcolo sia per quanto riguarda l’attendibilità del risultato (metodo dell’→ attrattore; metodo di → bisezione; metodo di → Newton (delle tangenti); metodo delle → secanti). Se l’errore che si commette con un particolare algoritmo a un passo dell’iterazione è proporzionale all’errore commesso nel passo precedente, si parla di convergenza lineare dell’algoritmo: il numero di cifre decimali esatte aumenta di un’unità a ogni passo. Se l’ordine di grandezza dell’errore è proporzionale al quadrato di quello commesso al passo precedente, si parla invece di convergenza quadratica dell’algoritmo: il numero di cifre decimali esatte raddoppia a ogni iterazione. CONVERGENZA DI UN ALGORITMO CONVERGENZA DI UN ALGORITMO CONVERGENZA DI UN ALGORITMO