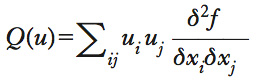convessità
convessita
convessità Concetto della matematica elementare, pura e applicata, il cui significato intuitivo fa parte del linguaggio quotidiano. In matematica si distingue tra problemi lineari e non lineari; mentre i primi sono facili da descrivere e qualche volta da risolvere, non è così per i secondi. Spesso, però, quando i problemi non lineari sono convessi, si può sperare di risolverli, o almeno di ricavare qualche loro proprietà.
Insiemi convessi
In uno spazio lineare X, un insieme K è detto convesso se, presi due punti k1 e k2 appartenenti a K, il segmento che li congiunge, cioè l’insieme dei punti tk1+(1−t)k2 tali che t∈[0,1], è tutto contenuto in K. Per es., nel piano sono insiemi convessi le comuni figure geometriche come triangoli, quadrati e cerchi, così come lo sono i loro analoghi in spazi di dimensione maggiore di due.
Funzioni convesse
Una funzione a valori reali V, definita su un sottoinsieme di uno spazio lineare X, viene detta convessa se per ogni x e y nel dominio della funzione e per ogni λ con 0≤λ≤1 si ha V(λx+(1−λ)y)≤λV(x)+(1−λ)V(y). Il legame tra i due concetti di c., per gli insiemi e le funzioni, può anche esprimersi dicendo che l’epigrafico di una funzione convessa (cioè l’insieme dei punti che stanno sopra il grafico) è un insieme convesso. Le funzioni convesse hanno molte proprietà di regolarità. La definizione stessa implica in particolare che il dominio di una funzione convessa debba essere convesso. Una funzione con derivata seconda continua è convessa se e soltanto se la derivata seconda è maggiore o uguale a 0 in ogni punto. Una funzione di più argomenti con tutte le derivate seconde continue è convessa se, e solo se, la forma quadratica
è non negativa, cioè se l’hessiano della funzione (➔ hessiano) è definito non negativo (➔ positivo definito). ● Una funzione convessa, inoltre, è tale che le sue derivate seconde esistono quasi ovunque. Una funzione convessa in un insieme chiuso e limitato ha sempre un punto di minimo e tale minimo è unico se la funzione è strettamente convessa. Questa particolare proprietà delle funzioni convesse è quella che distingue i problemi di ottimizzazione convessa tra tutti gli altri problemi di ottimizzazione non lineare. Una delle interessanti proprietà delle funzioni convesse è la cosiddetta disuguaglianza di Jensen (➔ Jensen, diseguaglianze di), che dice che la media di una funzione convessa è sempre maggiore o uguale della funzione convessa calcolata nel punto medio. Un caso particolare è la nota disuguaglianza delle medie EX2≥(EX)2, che si ottiene dalla funzione convessa f(X)=X2. Una funzione f, al contrario, si dice concava se per ogni x e y nel dominio della funzione e per ogni λ con 0≤λ ≤1 si ha V(λx+(1−λ)y)≥λV(x)+(1−λ)V(y). Equivalentemente, una funzione f è concava se −f è convessa. Da questa definizione si ricavano le principali proprietà di una funzione concava, come, per es., il fatto che la forma quadratica Q(u) definita dalle derivate seconde di f è, al contrario del caso in cui f è convessa, minore o uguale a zero.