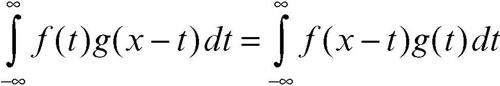convoluzione
convoluzione
convoluzione di due funzioni reali ƒ(x) e g(x) ∈ L1(R), è la funzione h(x) così definita:
La convoluzione è, quindi, l’integrale del prodotto tra le due funzioni, in cui una delle funzioni viene traslata dopo averne preso la simmetrica rispetto all’asse y. La convoluzione gode della proprietà commutativa:
Gode inoltre delle proprietà associativa e distributiva rispetto alla somma. La convoluzione di due funzioni dispari è dispari, mentre se almeno uno dei fattori è pari, tale è anche la loro convoluzione. La derivata di una convoluzione gode della seguente proprietà:
Eseguire la convoluzione di una funzione ƒ(t) con una funzione impulsiva δ(t – t0) centrata in t = t0 equivale a traslare nelle ascisse di t0 il grafico della funzione ƒ(t):
Vale infine il seguente teorema della convoluzione:
dove
rappresenta la trasformata di Fourier. Un analogo teorema sussiste anche per la trasformata di Laplace.