coordinate cartesiane
coordinate cartesiane
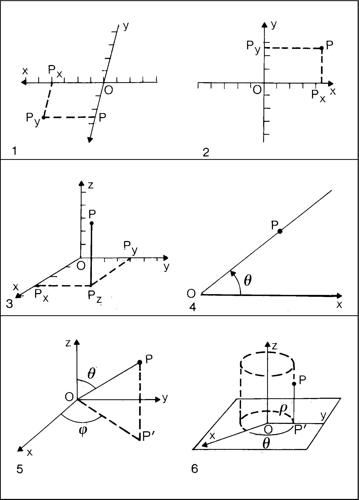
coordinate cartesiane o sistema di riferimento cartesiano, in geometria analitica, sistema di coordinate che su una retta r si ottiene fissando su di essa un verso di percorrenza (verso positivo), un punto O detto origine e un punto U detto punto unità, che segue O nel verso prefissato. Ciò consente di associare, in modo biunivoco, a ogni punto P ∈ r un numero reale x dato dalla misura con segno del segmento orientato OP, rispetto all’unità di misura OU. Il numero reale x è detto ascissa del punto P. Le ascisse sono le coordinate cartesiane dei punti della retta.
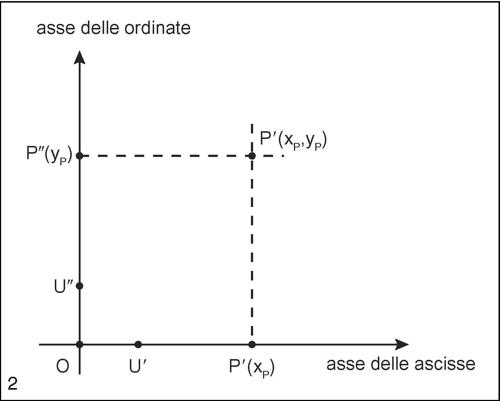
Per introdurre un sistema di coordinate cartesiane nel piano è necessario assegnare due rette incidenti in un punto O, ciascuna delle quali è detta asse cartesiano. Su ciascun asse viene fissato un sistema di ascisse, assegnando i punti unità e scegliendo O come origine. Se gli assi sono perpendicolari si ha un sistema di riferimento ortogonale. Se i segmenti unità hanno la stessa lunghezza si ha un sistema di riferimento monometrico. Ciò premesso, da un qualsiasi punto P del piano si tracciano le parallele agli assi cartesiani che incontrano gli assi nei punti P′ e P″, si indicano con xP e con yP, rispettivamente, le misure dei segmenti orientati OP′ e OP″ e si associa al punto P la coppia ordinata (xP, yP). Si viene così a stabilire una corrispondenza biunivoca tra i punti del piano e le coppie ordinate di numeri reali. I due numeri (xP, yP) sono le coordinate cartesiane del punto: la prima, genericamente indicata con la lettera x, è detta ascissa, la seconda, genericamente indicata con la lettera y, è detta ordinata. La retta OP′ è detta asse delle ascisse o asse x, l’altra retta è detta asse delle ordinate o asse y. Gli assi cartesiani sono anche detti assi coordinati e il sistema di riferimento è indicato con Oxy (o xOy, o XOY, o OXY).
Si chiama piano cartesiano un piano nel quale è stato introdotto un riferimento cartesiano. Gli assi coordinati dividono il piano cartesiano in quattro regioni, ciascuna delle quali è detta quadrante. Il primo quadrante è quello al quale appartengono i punti con entrambe le coordinate positive. I successivi quadranti si ottengono a partire dal primo ruotando in senso antiorario. Tracciando le bisettrici dei quadranti, il piano viene suddiviso in otto regioni, ciascuna delle quali è detta ottante. Gli ottanti sono numerati sempre procedendo in senso antiorario.
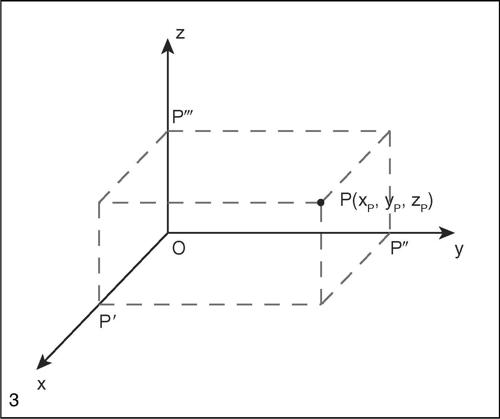
La procedura per introdurre un sistema di riferimento cartesiano si può estendere allo spazio ordinario o a uno spazio di dimensione n. Nello spazio ordinario un riferimento cartesiano Oxyz è costituito da tre rette orientate non complanari concorrenti in un punto O, ciascuna dotata di un sistema di ascisse di origine O. Le tre rette sono chiamate asse x, asse y, asse z. I tre piani che i tre assi coordinati individuano a due a due vengono detti piani coordinati. Generalmente il sistema scelto è ortogonale monometrico. Procedendo in analogia con il piano, da un qualsiasi punto P dello spazio si conducono i tre piani paralleli ai piani coordinati, si considerano le loro intersezioni P′, P″, P‴ con gli assi del riferimento e si indicano rispettivamente con xp, yp zp le misure dei segmenti orientati OP′, OP″, OP‴. Si stabilisce in tal modo una corrispondenza biunivoca tra i punti dello spazio e le terne ordinate di numeri reali. I tre numeri che costituiscono tali terne si dicono coordinate cartesiane e prendono il nome di ascissa (x), ordinata (y), quota (z).
Più in generale, in uno spazio vettoriale di dimensione n e base (u1, u2, …, un) le coordinate cartesiane di un qualsiasi punto P sono le componenti del vettore
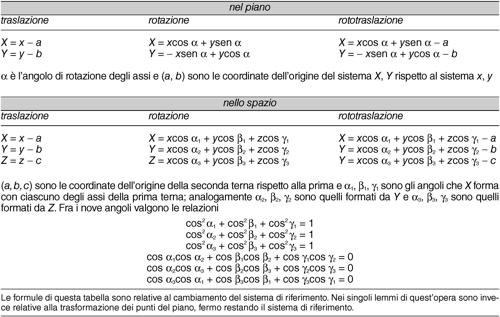
rispetto alla base. Se i vettori della base risultano a due a due ortogonali e tutti di modulo unitario, il riferimento è detto riferimento ortonormale. Poiché il sistema di riferimento scelto è arbitrario, è possibile e, in alcune situazioni, opportuno cambiarlo: si avrà di conseguenza un cambiamento di coordinate (→ riferimento, cambiamento di).