coordinate curvilinee

coordinate curvilinee

LettC_06060.rtf

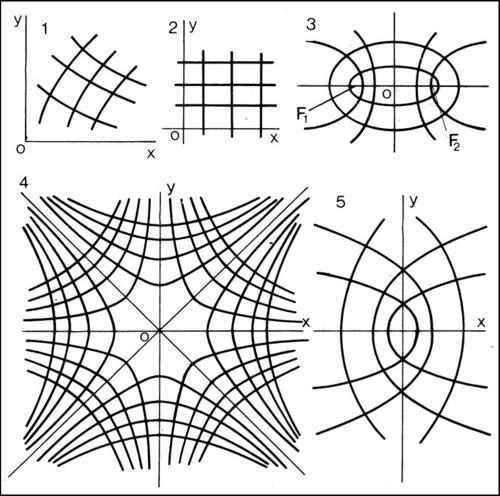
coordinate curvilinee in geometria analitica, sistemi di curve del piano tali che si possa stabilire una corrispondenza biunivoca e continua tra l’insieme dei punti P del piano e le coppie ordinate di curve (una del primo e una del secondo sistema) le quali si incontrino in un solo punto del piano. Le coordinate cartesiane costituiscono un caso particolare di coordinate curvilinee: i due sistemi di curve sono i fasci di rette parallele agli assi. Altri casi di coordinate curvilinee sono le coordinate bipolari (i due sistemi di curve sono cerchi con centro in due punti fissi o fuochi O₁ e O₂ e raggio variabile); le coordinate ellittiche (i due sistemi di curve sono coniche aventi tutte gli stessi fuochi F₁ e F₂: il primo sistema è costituito da ellissi, il secondo da iperboli); le coordinate iperboliche (i due sistemi sono iperboli equilatere, e gli asintoti del secondo sistema formano un angolo di 45° con quelli del primo; questo sistema è usato in pratica in vari sistemi di radionavigazione: i sistemi di iperboli hanno infatti in questi casi caratteristiche matematiche che si adeguano molto bene alle necessità pratiche); le coordinate paraboliche (i due sistemi sono parabole con le concavità rivolte in senso opposto nel secondo sistema rispetto al primo e aventi tutte i vertici sulla stessa retta; le parabole dei due sistemi sono simmetriche rispetto a una perpendicolare alla retta dei vertici).