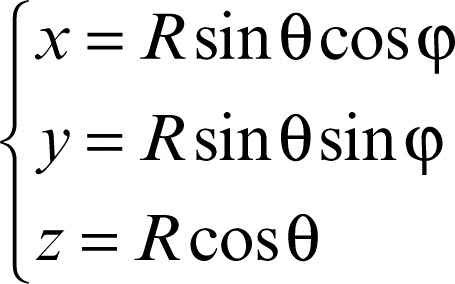Lagrange, coordinate di
Lagrange, coordinate di
Lagrange, coordinate di o coordinate generalizzate, in meccanica analitica sono coordinate indipendenti tra loro che permettono di descrivere le configurazioni di un sistema soggetto a vincoli. Si consideri, per esempio, un punto materiale vincolato a muoversi sulla superficie di una sfera di raggio R. Le tre coordinate cartesiane che descrivono la posizione del punto non sono indipendenti tra loro perché devono soddisfare la relazione x 2 + y 2 + z 2 = R 2 e questo complica lo studio della dinamica del sistema. Tuttavia, le configurazioni del sistema possono essere descritte mediante due coordinate indipendenti tra loro quali, per esempio, l’angolo di inclinazione θ e l’angolo azimutale φ, che sono legati alle coordinate cartesiane mediante le relazioni
e che possono essere invertite per ottenere le nuove coordinate in funzione delle vecchie. In generale, un sistema di n particelle non vincolate ha 3n gradi di libertà ed è descritto da altrettante coordinate cartesiane. Un vincolo su tale sistema è detto olonomo se esso non dipende dalle velocità, cioè se può essere descritto con una relazione del tipo ƒ(r1, r2, …, rn, t) = 0 dove ri è il vettore che ha per componenti le tre coordinate cartesiane dell’i-esima particella. Se il sistema è soggetto a k vincoli olonomi, esso ha 3n − k gradi di libertà e le sue configurazioni possono essere descritte tramite 3n − k coordinate lagrangiane, legate alle coordinate cartesiane da n equazioni vettoriali del tipo ri = ri (q1, q2, …, q3n−k, t), con i = 1, …, n . Si noti che in generale le coordinate lagrangiane non possono essere raggruppate in vettori di tre coordinate come accade per le coordinate cartesiane (→ lagrangiana).