coordinate sferiche
coordinate sferiche
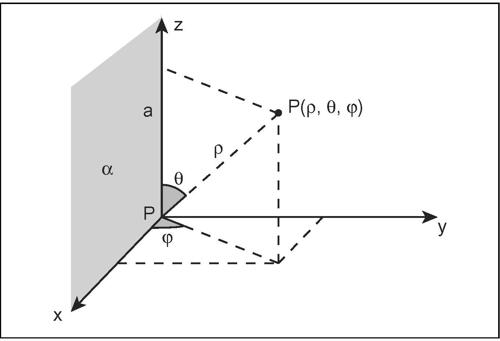
coordinate sferiche sistema di coordinate nello spazio tridimensionale costruito in modo analogo al sistema di coordinate polari per il piano. Fissato un punto O detto polo, una semiretta a uscente da O, detta asse polare e un semipiano α, uscente da a, detto semipiano polare, ogni punto P dello spazio viene individuato da una terna di numeri (ρ, θ, φ) che assumono il seguente significato: ρ è la misura del segmento OP, ossia la distanza del punto P dal polo O; θ è l’angolo formato dalle due semirette a e OP e φ è l’angolo formato dai semipiani α e aP. I tre numeri ρ ≥ 0, θ compreso tra 0 e π, φ compreso tra 0 e 2π, sono le coordinate sferiche di P e vengono dette, rispettivamente, raggio vettore, colatitudine o distanza zenitale, longitudine o azimut.
Il passaggio dalle coordinate sferiche a quelle cartesiane e viceversa è espresso dalle seguenti formule di trasformazione:
con ρ ≥ 0, θ ∈ [0, π], φ ∈ [0, 2π). Va osservato che φ = arctan(y/x), con la convenzione usata, vale solo nel primo quadrante; nel secondo e terzo vale φ = arctan(y/x) + π, mentre nel quarto vale φ = arctan(y/x) + 2π.