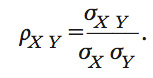covarianza

covarianza

Misura della relazione di concordanza di due variabili casuali X e Y. Essa è indicata con Cov(X,Y) o con σ_XY ed è definita dal momento centrato misto, ossia σ_XY=E(X−μ_X)(Y−μ_Y), dove μ_X e μ_Y sono uguali alle medie delle variabili X e Y. Un modo equivalente di definirla è σ_XY=E(XY)−μ_Xμ_Y, ossia come differenza tra la media del prodotto e il prodotto delle medie di X e Y. Come caso particolare, Cov(X,X)=σ²_X. La c. è una misura che può variare da −∞ a +∞ ed è sensibile ai cambiamenti di scala delle variabili X e Y. Infatti, se a è un’arbitraria costante diversa da 0, Cov(aX,Y)=aσ_XY.

La correlazione

Una misura indipendente dall’ordine di grandezza delle variabili casuali è la correlazione, indicata con Corr(X,Y) o con ρ_XY. Questa si ottiene dalla standardizzazione della c. σ_XY, ossia dalla divisione per la radice quadrata delle varianze di X e di Y, σ²_X e σ²_Y:

La correlazione è invariante rispetto alle trasformazioni lineari. In altre parole, per una qualsiasi costante a, Corr(aX,Y)=ρ_XY. Come conseguenza della disuguaglianza di Cauchy-Schwartz, secondo la quale

[E(X−μ_X)(Y−μ_Y)]²≤E(X−μ_X)²(Y−μ_Y)²,

si ha che la correlazione ρ_XY è sempre tale che ρ²_XY≤1. In particolare, ρ²_XY=1 se e solo se σ²_XY =σ²_Xσ²_Y, il che accade se e soltanto se X−μ_X e Y−μ_Y sono tra loro proporzionali. Ciò equivale a dire che la correlazione è una misura dell’esistenza di una relazione di tipo lineare tra le variabili casuali X e Y. Più precisamente, ρ_XY=1 equivale a una relazione lineare esatta e positiva tra X e Y, o a una perfetta concordanza, mentre ρ_XY=−1 coincide con una relazione lineare negativa, o perfetta discordanza tra le variabili casuali X e Y. Il caso ρ_XY=0 testimonia una assenza di relazione lineare tra X eY, ma non va confuso con indipendenza statistica tra le due variabili. È infatti possibile che due variabili X e Y, pur essendo legate da una relazione di forte dipendenza, abbiano correlazione uguale a 0. Due variabili per le quali ρ_XY=0 si dicono incorrelate. Un esempio di variabili incorrelate, ma non indipendenti è il seguente: sia Y una variabile aleatoria che assume i valori {−1,0,1}, con probabilità pari a 1/3,1/3,1/3, mentre X è definita da X=Y². In questo caso, X e Y non sono indipendenti, essendo il valore di X funzione di Y. Ciononostante, si ha μ_Y=0, μ_X=2/3 e σ_XY=0.

Se non è vero in generale che due variabili incorrelate sono tra loro indipendenti, è però vero che due variabili indipendenti sono sempre incorrelate (ammesso che i loro momenti secondi siano finiti). Una peculiarità della distribuzione gaussiana (➔ gaussiana, distribuzione) sta nel fatto che per una coppia (X,Y) con distribuzione normale bivariata, se X eY sono incorrelate, allora sono anche indipendenti. In tutti gli altri casi, la correlazione non è una misura di dipendenza statistica tra due variabili, ma la presenza di correlazione esclude l’indipendenza.

Nei casi intermedi, 0<ρ²_XY<1, un coefficiente di correlazione positivo indica concordanza tra le variabili, mentre uno negativo indica discordanza. Intuitivamente, la covarianza σ_XY è positiva se i prodotti (X−μ_X)(Y−μ_Y) di segno positivo hanno peso maggiore di quelli di segno negativo.

In un modello di regressione semplice, con un solo regressore, Y=α+βX+U, il coefficiente angolare della retta di regressione β è proporzionale a ρ_XY, essendo β=ρ_XY∙σ_Y/σ_X.