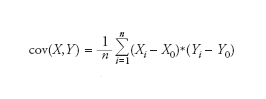covarianza

covarianza

Indice che permette di verificare una relazione lineare tra due variabili statistiche, X e Y. Dato un insieme di n rilevazioni statistiche (X₁,Y₁),(X₂,Y₂),...,(X_ν,Y_ν) la covarianza è definita nel modo seguente:

dove X₀ e Y₀ indicano il valore medio delle due variabili statistiche, X e Y, rispettivamente, e n rappresenta la grandezza del campione. La covarianza misura come le due variabili si discostano dai loro valori medi. Il segno della covarianza permette di dire se le fluttuazioni intorno alla media delle due variabili sono concordi o discordi. Una covarianza positiva implica che la maggior parte dei termini nella somma sono positivi, cioè le variazioni di X e Y rispetto ai loro valori medi hanno lo stesso segno. Si parla dunque di variazioni concordi. Al contrario, una covarianza negativa implica che la maggior parte dei termini nella somma ha segno negativo e quindi che i due termini, (X−X₀) e (Y−Y₀), hanno segno opposto. Le due variabili fluttuano intorno ai loro valori medi in modo discorde. La covarianza permette di definire un coefficiente di correlazione, detto coefficiente di Pearson: r_Χϒ=cov(X,Y)/cov(X)*cov(Y). Questo coefficiente è utilizzato per misurare la correlazione lineare tra due variabili statistiche facendo riferimento a una scala assoluta. Il coefficiente r_Χϒ è per definizione sempre compreso tra i valori −1 e 1. L’esistenza di correlazione lineare implica r=1 o −1. Due variabili non correlate saranno associate a r_Χϒ=0.

→ Atmosfera. Lo strato limite