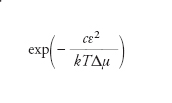crescita a strati
crescita a strati
Modo di crescita di un cristallo, detto anche modo di Frank-van der Merwe, caratterizzato da un’estrema regolarità del processo di accrescimento, nel quale la superficie del solido è un piano cristallografico, anche se spesso diverso dai piani cristallografici interni (la superficie è rilassata, cioè si trova a una distanza dal secondo strato diversa da quella che si stabilisce all’interno della struttura cristallina, e può essere ricostruita, cioè può avere una struttura bidimensionale anch’essa diversa). Durante la crescita, su un primo strato se ne deposita un secondo, poi, quando questo è completo o quasi, comincia a formarsene un terzo. Ogni strato si forma a partire da isole bidimensionali che si uniscono (dando luogo a coalescenza). La formazione di tali isole è un processo non facile e spesso lento, perché energeticamente dispendioso (è dispendiosa, infatti, la formazione del bordo di un’isola). Già negli anni Trenta del Novecento, Richard Becker e Werner Döring formularono una teoria semplice e convincente di tale processo, cui qui accenniamo in una formulazione ancora più semplice. A ciascuna delle isole bidimensionali, di perimetro l e area A, che si formano su uno strato cristallino già depositato si può associare un’energia libera di Gibbs che consta essenzialmente di due termini: un termine positivo lε che corrisponde al costo del bordo (dove ε è il costo energetico per unità di lunghezza del gradino, di altezza h, che costituisce il bordo) e un termine negativo −AhϱΔμ (dove ϱ è la densità del cristallo e Δμ è la differenza di potenziale chimico tra fluido e cristallo), che corrisponde al guadagno energetico ottenuto dalla formazione dell’isola. Poiché l è proporzionale al diametro dell’isola e invece A al suo quadrato, le isole piccole hanno un’energia libera positiva e sono sfavorite, mentre le grandi comportano un guadagno energetico. Occorre perciò superare una barriera, rappresentata dall’energia libera dell’isola più sfavorevole. L’altezza della barriera energetica è cε2/Δμ (dove c è un fattore geometrico), e la probabilità che sia superata, quindi che il cristallo cresca, è proporzionale al fattore di Boltzmann
In condizioni vicine all’equilibrio Δμ è piccolo e la probabilità di crescita è esponenzialmente piccola: di fatto, nessuna crescita a strati dovrebbe essere possibile. In realtà, invece, gli esperimenti dimostrano che la crescita a strati avviene benissimo in condizioni vicine all’equilibrio: la velocità di crescita in certi casi è anche 1030 volte più grande di quella predetta dalla teoria di Becker e Döring. Questo paradosso costituì un grave problema per parecchi anni. L’enigma fu risolto da Frederick C. Frank. La teoria di Becker e Döring era corretta per un cristallo perfetto; ma, se nel cristallo è preesistente una dislocazione a vite, la crescita può avvenire con costo energetico minimo avvolgendo a spirale la dislocazione, senza bisogno di formare nuove isole. Questa crescita a spirale assume quindi grande importanza quando Δμ è piccolo.