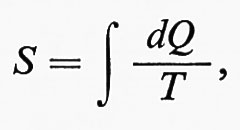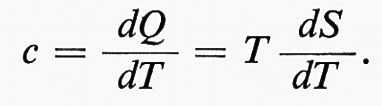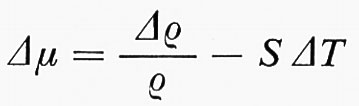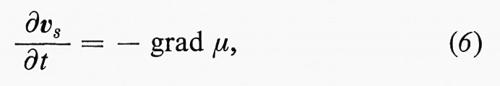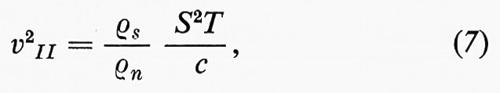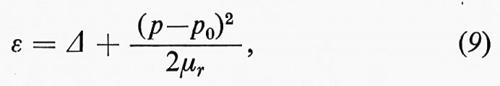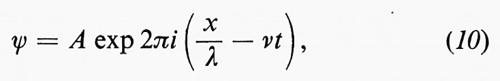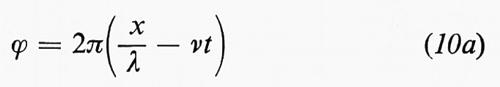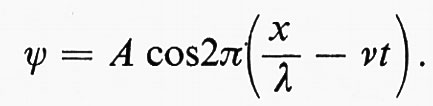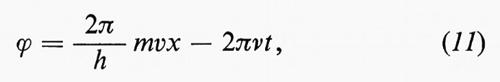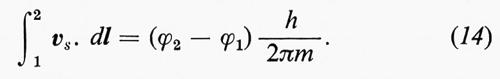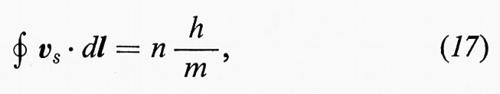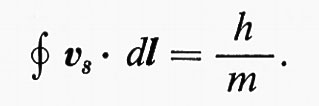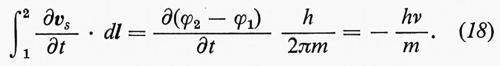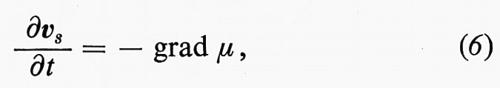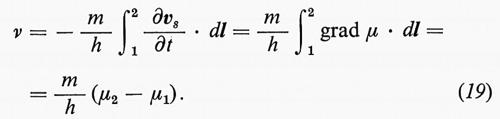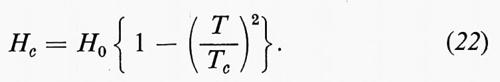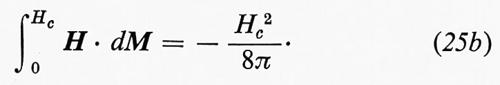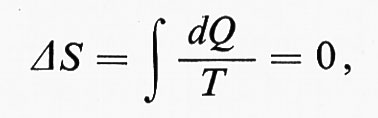Criofisica

Criofisica

di Cornelis J. Gorter e W. J. Huiskamp, D. de Klerk, H. C. Kramers

SOMMARIO: 1. Introduzione: a) definizione; b) la ‛preistoria'; c) lo sviluppo dei laboratori per le basse temperature; d) la disponibilità e la conservazione dell'elio; e) l'importanza delle basse temperature per la fisica; f) i termometri. □ 2. La fisica alle basse temperature: a) relazione tra termodinamica e basse temperature; b) solidi; c) conclusione. □ 3. Elio quattro liquido e superfluidità: a) elio quattro liquido; b) il modello a due fluidi dell'elio IL; c) osservazioni spiegate dal modello; d) il fondamento del modello a due fluidi; e) gli aspetti quantomeccanici del superfluido; f) linee vorticose quantizzate; g) l'interferenza quantistica nell'elio liquido. □ 4. La superconduttività: a) introduzione; b) il campo di perturbazione e l'effetto Meissner; c) considerazioni termodinamiche; d) il modello a due fluidi; e) la teoria di London; f) la lunghezza di coerenza; g) superconduttori di tipo II; h) teoria microscopica della superconduttività; i) effetto tunnel; l) effetti Josephson e interferenza quantistica. □ 5. Temperature ultrabasse: a) metodi di raffreddamento; b) proprietà dell' ³He; c) orientazione nucleare; d) termometria, equilibrio termico e fluttuazioni termiche. □ 6. Applicazioni tecniche e sviluppi futuri. □ Bibliografia.

1. Introduzione.

a) Definizione.

La criofisica, cioè la fisica delle basse temperature, può essere definita in vari modi. All'inizio, essa comprendeva tutte le ricerche a temperature inferiori, diciamo, a quella ambiente, mentre adesso, negli anni settanta, si sogliono in essa comprendere soltanto quei fenomeni che avvengono al di sotto del punto di ebollizione dell'elio, al di sotto, cioè, di −268,94 gradi Celsius, pari a 4,2 gradi sopra lo zero assoluto (4,2 Kelvin, abbreviato 4,2 °K). D'altra parte, però, in essa vanno inclusi anche fenomeni, come la superconduttività, che si producono al di sopra di questo punto: estendendo al massimo la definizione, il limite superiore della criofisica può essere fissato in 20 °K. Nel corso del tempo, inoltre, molti rami della fisica hanno avuto un importante sviluppo alle basse temperature, mentre altri argomenti che pure facevano inizialmente parte della criofisica sono diventati materia di studio a sé stante e le loro caratteristiche principali non sono più considerate legate alle basse temperature. Alcuni di questi argomenti saranno trattati brevemente nel cap. 2.

Vi sono due campi che appartengono decisamente alle basse temperature: la superfluidità dell'elio liquido (v. cap. 3) e la superconduttività (v. cap. 4). Questi fenomeni saranno trattati un po' più estesamente poiché presentano molti aspetti fondamentali della fisica che ricorrono soltanto alle basse temperature.

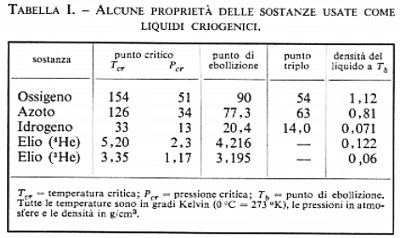
Per studiare le proprietà della natura, la cosa migliore è avere a disposizione un ‛bagno' di un liquido che possa essere mantenuto a temperatura costante semplicemente regolando e mantenendo costante la pressione del vapore sopra di esso. Questo si può fare facilmente per pressioni comprese tra 1 atm (la pressione normale di ebollizione) e il ‛punto triplo', al di sotto del quale il liquido solidifica. Gli intervalli di temperatura adatti a questo sono la regione dell'azoto (78 °K-63 °K), quella dell'idrogeno (20 ⁰K-14 °K) e quella dell'elio (4,2 °K-1,0 °K). Il limite inferiore dell'elio non è dovuto alla sua solidificazione, ma all'impossibilità pratica di ottenere pressioni di vapore più basse. Negli ultimi anni la disponibilità in quantità sufficienti dell'isotopo dell'elio ³He, non comune in natura, ha permesso di scendere un gradino più in basso, a 0,3 °K, ma peraltro la regione al di sotto di °K richiede ancora delle tecniche particolari, anche se negli anni sessanta sono stati compiuti dei progressi notevoli. Ci è sembrato pertanto opportuno riservare a questa gamma di temperature una trattazione separata (v. cap. 5).

Nel cap. 6, infine, parleremo dell'influenza delle basse temperature sulle tecnologie usate in altri campi della scienza e sulla società in generale, sia per il presente sia per il futuro.

In questo primo capitolo esamineremo brevemente lo sviluppo storico, con particolare riguardo per il processo di liquefazione.

b) La ‛preistoria'.

È ben noto che un gas può essere liquefatto mediante compressione isotermica, purché la temperatura sia inferiore alla cosiddetta temperatura critica. Dopo isolamento termico, si può ridurre la pressione sul liquido e abbassare così la temperatura. Con questo sistema, impiegato a temperature via via più basse (metodo a cascata), si arrivò alla liquefazione dell'ossigeno e dell'azoto (P. Cailletet, 1877).

Questo sistema non può essere adoperato per l'idrogeno e per l'elio perché le loro temperature critiche sono notevolmente più basse di quelle minime ottenibili con altre sostanze (si confrontino, nella tab. I, i valori delle T_cr con i punti tripli dell'azoto e dell'ossigeno).

Per la comprensione del significato di temperatura critica e per lo sviluppo di nuovi metodi per la liquefazione dei restanti ‛gas permanenti', fu essenziale il lavoro di J. D. Van der Waals culminante nell'equazione di stato dei gas e dei liquidi con interazione. Egli trovò che l'interazione tra le molecole dei gas e dei liquidi consiste di una parte repulsiva, che agisce a distanze brevi, e di una parte attrattiva, il cui raggio d'azione è alquanto più lungo. Al di sopra della temperatura critica non vi è nessuna pressione (cioè nessuna distanza media tra le molecole) per cui l'attrazione sia sufficiente a superare la repulsione o l'effetto del moto termico; di conseguenza le molecole non rimangono mai insieme come in un liquido. Al di sotto della temperatura critica esistono sempre siffatti valori della pressione.

Tuttavia, anche al di sopra della temperatura critica, si possono sfruttare le forze di attrazione per compiere lavoro a spese dell'energia interna, a patto che non si usino pressioni troppo alte. È questo il cosiddetto ‛effetto Joule-Kelvin' che è servito per la liquefazione dell'idrogeno e dell'elio. In un apparecchio termicamente isolato, il gas compresso e preraffreddato viene fatto espandere attraverso una valvola regolatrice di flusso. La riduzione dell'energia interna del gas è accompagnata da una diminuzione della temperatura: questo effetto è però efficace soltanto se la temperatura iniziale è sufficientemente bassa; a temperature più alte, infatti, il risultato può anche essere contrario a quello voluto e dar luogo a un riscaldamento.

La liquefazione dell'idrogeno fu ottenuta in questo modo per la prima volta nel 1898 da Dewar e finalmente il 10 luglio 1908 Kamerlingh Onnes riuscì a produrre elio liquido (v. fig. 1). Perché l'effetto Joule-Kelvin producesse un raffreddamento, fu necessario preraffreddare l'elio con idrogeno liquido.

Non è nostra intenzione addentrarci qui nei procedimenti tecnici della liquefazione, dobbiamo però accennare a due punti importanti. In primo luogo, il necessario isolamento termico fu reso possibile grazie all'introduzione da parte di Dewar del recipiente, che porta il suo nome, a doppia parete di vetro con intercapedine vuota e pareti argentate a evitare l'irraggiamento. Inoltre, un efficiente procedimento di raffreddamento continuo è possibile soltanto se il gas in entrata è preraffreddato, in un apposito scambiatore di calore, dal gas freddo di ritorno. Senza queste invenzioni iniziali, la criofisica non sarebbe neppure concepibile.

c) Lo sviluppo dei laboratori per le basse temperature.

Dal 1911 fino al 1923, anno in cui McLennan costruì un liquefattore a Toronto, il laboratorio di Leida era l'unico luogo nel mondo dove fosse disponibile l'elio liquido. Il numero di laboratori per le basse temperature rimase invero abbastanza piccolo fino alla seconda metà degli anni trenta: a Berlino nel 1925 sorse il laboratorio di Meissner, a Oxford nel 1933 quello di Lindemann, Keeley e Simon, a Cambridge, in Inghilterra, nel 1934 quello di P. L. Kapica, a Berkeley nel 1935 quello di Giauque, a Khar'kov nel 1936 quello di Subnikov e a Mosca nel 1938 ancora un altro di Kapica. Durante questo periodo furono apportati molti miglioramenti alla tecnica di liquefazione, il più importante dei quali fu l'introduzione, apportata da Kapica, del liquefattore con motore a espansione. Il gas in espansione è costretto a compiere lavoro esterno agendo sui pistoni di un motore. Contrariamente a quanto si verifica nell'effetto Joule-Kelvin di espansione nel vuoto, ciò dà sempre luogo a una riduzione della temperatura; così è sufficiente il preraffreddamento mediante azoto liquido, senza che si debba ricorrere allo stadio intermedio dell'idrogeno liquido. Nelle macchine di tipo più recente si può fare a meno anche del preraffreddamento ad azoto, a costo, però, di una produzione leggermente inferiore. Bisogna anche accennare al fatto che il principio del lavoro esterno è ormai d'uso normale anche nella produzione di azoto e aria liquidi.

Subito dopo la seconda guerra mondiale, la macchina di Kapica fu migliorata da Collins al Massachusetts Institute of Technology e fu messa in commercio dalla Arthur D. Little Company di Boston. Da allora, il numero di laboratori per le basse temperature, o meglio di laboratori dotati di macchine per la produzione di elio liquido, è aumentato enormemente: la trecentesima macchina di Collins fu installata nel 1965 a St. Andrews in Scozia. Uno sviluppo analogo si è avuto anche nell'Europa orientale, dove una macchina di Kapica migliorata è divenuta ormai di normale dotazione dei laboratori.

Negli anni sessanta vi fu un ulteriore sviluppo: il miglioramento delle tecniche di isolamento rese infatti possibile la conservazione dell'elio liquido per periodi notevolmente più lunghi, permettendone il trasporto anche a grandi distanze. Oggi è più conveniente trasportare l'elio come liquido che come gas compresso in bombole, anche per distanze molto grandi come quelle che intercorrono tra gli Stati Uniti e l'Europa.

Grossi impianti di liquefazione in vari paesi vendono oggi il liquido a un numero sempre crescente di laboratori, i quali trovano più conveniente acquistare il liquido piuttosto che liquefare il gas sul posto. I nuovi grossi impianti, che ora usano prevalentemente motori a turbina, hanno una produzione dell'ordine di 1.000 litri per ora che può andare avanti per delle settimane. Questa cifra può essere paragonata alla produzione di 0,25 litri per ora del primo liquefattore di Kamerlingh Onnes, il quale tra l'altro poteva funzionare solo per un tempo limitato a causa dei problemi di purificazione e della scarsa quantità di elio allora disponibile.

Per molti laboratori di ricerca è ancora conveniente avere un proprio liquefattore: il laboratorio Kamerlingh Onnes a Leida (v. fig. 2) usa ora un liquefattore Philips con una produzione continua di 12,5 litri per ora; il consumo annuo di elio liquido in quel laboratorio è, al presente, di 60.000 litri.

D'altra parte, vi è una richiesta crescente di piccoli liquefattori che lavorino con continuità sul principio del circuito chiuso di elio. Questa richiesta potrebbe diventare considerevole se alcune delle applicazioni tecnologiche trattate nel cap. 6 dovessero divenire di più larga diffusione.

d) La disponibilità e la conservazione dell'elio.

L'unico modo economico di ottenere l'elio è di ricavarlo come prodotto secondario nel processo di estrazione del gas naturale. Le sorgenti più ricche negli Stati Uniti contengono l'1% di elio, ma normalmente esso si trova in percentuali assai minori, di qualche parte su 1.000 o su 10.000.

Fino a oggi per ricerche di criofisica viene consumata meno del 10% della produzione annua di elio, ma la situazione potrebbe cambiare se le applicazioni della superconduttività (v. sotto, cap. 6) dovessero acquistare maggiore importanza nella società umana. Non c'è pertanto da stupirsi che i fisici siano preoccupati per la disponibilità futura dell'elio: infatti, soltanto una parte di quello che si trova nel gas naturale prodotto per ottenere energia viene conservato, mentre tutto quello che proviene da sorgenti a bassa percentuale va irrimediabilmente perduto. Un programma di conservazione dell'elio, redatto a cura del governo degli Stati Unitì e ispirato a una mozione della Conferenza internazionale sulla criofisica del 1957, prevedeva l'immagazzinamento di grosse quantità di elio in pozzi di gas vuoti. In tal modo rimarrebbe disponibile per il futuro la produzione presente, che è ora troppo abbondante a causa della grande produzione di gas naturale. Purtroppo, il futuro di questo programma appare ancora incerto.

e) L'importanza delle basse temperature per la fisica.

In senso molto generale si può dire che l'energia termica, la quale alle alte temperature nasconde completamente la maggior parte degli effetti fisici più sottili, si riduce alle basse temperature. L'energia termica di una molecola è dell'ordine di kT, dove k è la costante di Boltzmann (1,4.10^-23 joule /°K) e T è la temperatura assoluta. Le proprietà in cui intervengono energie molto piccole sono osservabili soltanto se kT è dell'ordine di tali energie o più piccolo, cioè alle basse temperature. Questi studi si rivelano quindi essenziali per una conoscenza approfondita di molte proprietà fondamentali della materia. La meccanica quantistica, che nacque dagli studi di spettroscopia, si sviluppò come ricerca sulle basse temperature. Si può dire che la nostra conoscenza della natura ha molto profittato delle interazioni tra la teoria quantistica e le ricerche di criofisica. Un gran numero di esperimenti ha portato a nuovi concetti nella meccanica quantistica e a una migliore comprensione dei fondamenti quantomeccanici della natura. Nei paragrafi che seguono ne saranno dati alcuni esempi.

f) I termometri.

È evidente che la determinazione della temperatura ha un'importanza fondamentale nello studio della criofisica. Come termometro di base, strettamente legato alla definizione termodinamica di temperatura, è stato molto usato il termometro a gas.

Per un gas diluito, e per valori della pressione bassi rispetto alla pressione del vapore, vale con buona approssimazione l'equazione di stato dei gas perfetti:

PV = costante × T.

Sono così necessarie soltanto misure di pressione (P) e di volume (V) per la determinazione della temperatura. Le deviazioni da questa equazione si possono determinare con sufficiente accuratezza.

Il termometro a gas non è però molto pratico da usare e di conseguenza si preferisce adoperare dei termometri secondari che siano stati inizialmente tarati con dei termometri a gas. Evidentemente, a questo scopo ci si può servire di una qualunque grandezza fisica che vari in maniera apprezzabile al variare della temperatura.

La scala delle temperature attorno ai valori della temperatura dell'elio liquido è fissata da una tavola di dati sulla pressione del vapore riconosciuta in sede internazionale. Questa tavola è stata compilata dopo un attento confronto dei valori ottenuti in vari laboratori specializzati.

Il numero dei termometri secondari disponibili è piuttosto elevato. Una grandezza fisica molto utile per la misura della temperatura è la resistenza dei metalli puri e dei semiconduttori. Con il platino si ottiene un termometro a resistenza facilmente riproducibile e utilizzabile al di sopra della regione dell'elio. A temperature più basse, invece, la resistenza dipende troppo poco dalla temperatura.

La conducibilità dei semiconduttori è dovuta a degli elettroni che devono essere ‛liberati' dal moto termico in modo da poter partecipare alla conduzione; perciò, la resistenza alle basse temperature tende all'infinito, con un andamento che dipende grandemente dalla presenza di impurità. Ciò significa che, con una scelta opportuna, si possono ottenere dei termometri molto sensibili in qualsiasi intervallo di temperature. Le normali resistenze a carbonio si usano alle volte con buon profitto per temperature nella regione dell'elio, ed al di sotto di essa, anche se presentano problemi di riproducibilità. Più stabili, anche se più costosi, sono i termometri a germanio. Un certo numero di termometri più sofisticati sarà trattato più avanti nel cap. 5, dedicato alle temperature ultrabasse.

2. La fisica alle basse temperature.

a) Relazione tra termodinamica e basse temperature.

L'evoluzione della criofisica è strettamente legata all'evoluzione delle teorie della meccanica statistica sul comportamento di insiemi di atomi o di molecole, quali sono i gas, i liquidi e i solidi. La liquefazione dei gas fu ottenuta all'epoca in cui Van der Waals dedusse l'equazione, che ora va sotto il suo nome, sulla base di una concezione molecolare dei gas e dei liquidi. All'inizio del secolo, la teoria statistica di Boltzmann e Maxwell segnò un momento assai importante nello sviluppo della fisica. Contemporaneamente, ma in un certo senso indipendentemente da queste teorie atomistiche, si andava sviluppando la termodinamica sulla base di pochi postulati (detti anche le tre ‛leggi della termodinamica').

1. L'energia si conserva e il calore è una particolare forma di energia. Per esempio, un gas che si espanda muovendo un pistone contro una pressione esterna tende a raffreddarsi, convertendo, in questo processo, calore in lavoro meccanico (v. sopra, cap. 1, È c: liquefattore di Kapica).

2. Il calore non può passare spontaneamente da un corpo freddo a uno caldo. Per far passare del calore da un corpo freddo a uno caldo è necessario compiere del lavoro, per esempio il lavoro meccanico W compiuto da un pistone. Questo è un aspetto fondamentale di tutti i metodi di raffreddamento, in particolare anche di quelli descritti nel cap. 5. Al calore Q₁ preso dal corpo freddo a temperatura T₁ è necessario aggiungere l'energia meccanica W perché dal corpo caldo venga assorbito, come calore, Q₂ = Q₁ + W. Se si fa in modo che il processo sia reversibile, si ottiene la relazione Q₁/T₁ = Q₂/T₂. Tutto ciò può essere espresso come conservazione dell'entropia, dS₁ + dS₂ = 0, dove l'entropia è definita come

da cui TdS = dQ. In tal caso, dQ = −Q₁ per il corpo freddo e dQ = +Q₂ per quello caldo; l'entropia totale è costante. Se Q₁ dovesse essere uguale a Q₂, si dovrebbe avere dS= dS₁ + dS₂ 〈 0 se T₁ 〈 T₂.

Quindi il postulato di cui sopra può anche essere formulato dicendo che l'entropia totale S non può diminuire. S può crescere se si fa passare in maniera irreversibile il calore dal corpo caldo a quello freddo, dQ₁ > 0, dQ₂ = −dQ₁, dS = dS₁ + dS₂ > 0.

Nei processi termici l'entropia ha un ruolo tanto importante quanto quello dell'energia. Dal punto di vista della teoria cinetica, essa è legata al disordine; di contro, una situazione ordinata in cui tutte le particelle siano nello stato energetico più basso corrisponde all'entropia S = 0. Il concetto di entropia ha acquistato un significato più preciso dopo l'introduzione da parte di Planck del quanto di energia, che assegna, a ciascuna particella, dei livelli energetici discreti. Si consideri un sistema completamente ordinato (S = 0) di N particelle. Se esso assorbe dei quanti di energia, il che equivale a dire che la sua temperatura cresce, un certo numero di particelle passerà a un livello energetico più alto. È poco probabile che tutta l'energia disponibile venga assorbita da una sola particella, così come altrettanto poco probabile è che N quanti si distribuiscano tra N particelle.

L'entropia del sistema è proporzionale al logaritmo della probabilità che si realizzi una particolare distribuzione di energia fra N particelle. Poiché le collisioni tra particelle portano a uno scambio di energia, alla fine si avrà una situazione di massima entropia.

Se, per esempio, tutta l'energia fosse posseduta da una sola particella, le collisioni ristabilirebbero immediatamente una situazione più probabile, di maggiore entropia.

3. L'entropia di un sistema di particelle tende a zero allo zero assoluto. Questo postulato può essere formulato in modo quasi equivalente dicendo che lo zero assoluto non è raggiungibile.

Raffreddando un corpo fino a una temperatura T prossima a zero, qualsiasi dS = dQ/T porterebbe a un dQ infinitamente piccolo, al tendere di T verso 0. In altri termini, anche una quantità minima di calore somministrata al corpo farebbe aumentare enormemente l'entropia e ristabillrebbe una temperatura finita. Questa è una caratteristica fondamentale di tutte le esperienze condotte a basse temperature. Questo terzo postulato fu formulato da H. W. Nernst nel 1906 ed è anche noto come ‛teorema del calore di Nernst'. Esso equivale quasi ad affermare che il calore specifico di un corpo tende a zero quando T→ 0. Si ha dunque la relazione:

La terza legge della termodinamica ha avuto un ruolo importante nello sviluppo della meccanica quantistica. Per un sistema di molecole con livelli energetici discreti, la legge termodinamica può essere derivata dal concetto statistico di entropia. Nel 1906 Finstein, sulla base dell'ipotesi che le vibrazioni atomiche in un solido fossero rappresentate da oscillatori quantizzati, dimostrò che il calore specifico di un solido tende a zero per T → 0. Questo fu poco dopo dimostrato in maniera anche più rigorosa da P. J. Debye (1912), la cui previsione che fosse c ∝ T³ fu confermata da esperimenti condotti a basse temperature, come per esempio da quelli di Nernst e di A. T. Eucken. Dal momento che la teoria classica aveva previsto che i calori specifici sarebbero stati sostanzialmente costanti, queste scoperte confermarono l'ipotesi quantistica di Planck. In seguito, esperimenti più precisi rivelarono delle deviazioni dalla teoria di Debye che furono spiegate da M. Born e Th. von Kármán (1912) tenendo conto in maniera più rigorosa del carattere discreto del reticolo.

b) Solidi.

1. Metalli. - Alla fine del XIX secolo, quando la meccanica statistica, l'elettricità e il magnetismo erano al centro dell'attenzione dei fisici, si cercò di dare una spiegazione teorica del fenomeno della conduzione elettrica nei metalli. Si trovò che, come per il caso delle soluzioni elettrolitiche, le correnti elettriche dovevano essere prodotte dal moto di particelle cariche. La scoperta dell'elettrone spinse H. A. Lorenz, sulla base di precedenti risultati di P. Drude, a dare una descrizione quantitativa del fenomeno della conduzione. Si pensò che i metalli fossero composti di un reticolo cristallino di ioni a carica positiva in posizioni fisse, immersi in un gas di elettroni che potevano muoversi più o meno liberamente. Questa si dimostrò un'ipotesi fruttuosa che permetteva di spiegare perché i metalli sono buoni conduttori di elettricità; questo vale in particolare per i metalli monovalenti, che sono facilmente ionizzabili. Inoltre, dalla stessa ipotesi deriva il fatto che i metalli sono buoni conduttori di calore. Secondo la logica stringente della meccanica statistica dei gas, ai gradi di libertà del moto degli elettroni dovrebbe essere associata un'energia termica di ³₂- kT per particella. Più precisamente, questa semplice teoria prevedeva che il rapporto tra conduttività termica, K, e conduttività elettrica, σ, dovesse essere dato dall'espressione K/σ = LT, dove L, detto il ‛numero di Lorenz', è approssimativamente indipendente dal metallo specifico considerato e dalla temperatura. Questo era già stato comprovato sperimentalmente, in particolare da Wiedemann e Franz.

Tuttavia, all'energia termica posseduta dagli elettroni dovrebbe corrispondere un contributo alla capacità termica pari a ³₂- k per particella. Contrariamente a quest'ultima predizione, misure fatte da Eucken mostrarono che tale contributo degli elettroni alla capacità termica non esisteva, o al massimo era eguale all'1% del valore ³₂- k previsto. Gli esperimenti successivi di W. H. Keesom e A. Simon dimostrarono che alle basse temperature gli elettroni contribuivano alla capacità termica per una piccola quantità c_el ∝ γT. Tutto ciò rimase inesplicabile fino allo sviluppo della meccanica quantistica.

Inoltre si trovò che la conduttività elettrica cresceva alle basse temperature, ove alcuni metalli diventavano addirittura superconduttori (v. sotto, cap. 4): ciò era in contrasto con la teoria classica secondo cui il moto termico degli elettroni dovrebbe diminuire al decrescere di T. Studi quantitativi sulla conduttività elettrica in funzione della temperatura mostrarono che la impedenza al trasporto degli elettroni cresce proporzionalmente col numero di fononi, ossia delle vibrazioni reticolari. Si trovò che a temperatura molto bassa la resistenza diventa praticamente costante e dipende solo dalla concentrazione di impurità. In altre parole, il moto elettronico apparentemente è ostacolato dalle irregolarità del reticolo cristallino; la concezione classica secondo cui le collisioni con gli ioni del reticolo e con altri elettroni mobili avrebbero limitato la conduttività elettrica non concordava ovviamente con i risultati ottenuti alle basse temperature.

D'altra parte, si era anche trovato che gli elementi metallici, a parte alcune eccezioni come il ferro, non presentavano vistosi effetti magnetici. La suscettività magnetica, inoltre, era indipendente dalla temperatura, contrariamente a quanto si verificava per i composti magnetici. Era tuttavia difficile dubitare che gli elettroni liberi possedessero un momento angolare di spin (G. E. Uhlenbeck e S. A. Goudsmit, 1925) e un notevole momento magnetico e che perciò gli elettroni liberi dovessero presentare effetti di magnetismo. Questi problemi furono tutti insieme risolti dalla teoria quantistica di E. Schroedinger. L'idea di assegnare stati energetici discreti a una particella racchiusa in un volume delimitato, insieme col principio di Pauli secondo cui non più di due elettroni possono occupare lo stesso stato energetico, condussero Fermi a proporre una nuova teoria statistica applicata in seguito da A. Sommerferld alla descrizione del comportamento dei metalli. Divenne così immediatamente chiaro che gli elettroni non possono essere considerati alla stregua di particelle classiche che in un senso lontano, dal momento che anche a temperature di ≈10⁴ °K (molto superiori al punto di fusione dei metalli) essi occuperebbero solo gli stati energetici più bassi. Questo comporta, per esempio, che i loro spins sono accoppiati antiparallelamente, in modo da non contribuire alla suscettività magnetica. Solo gli elettroni non appaiati sulla ‛superficie di Fermi' contribuiscono al comportamento magnetico. In maniera analoga, questa teoria spiegava perché la capacità termica fosse relativamente piccola e proporzionale a T, come era stato trovato da Keesom, Simon e altri (v. sopra). Così si spiega facilmente anche il fatto che sono improbabili le collisioni tra elettroni (come diremo nel cap. 5 a proposito delle analoghe proprietà dell' ³He liquido). La verifica della statistica di Fermi si dimostrò in seguito di particolare importanza per l'accettazione della statistica di Bose-Einstein, cioè di quella che vale per particelle non soggette al principio di Pauli. Per quanto riguarda il comportamento dei solidi, un'analisi più raffinata dei livelli energetici in reticoli periodici di ioni fornì misure precise delle bande energetiche e condusse quindi alle ricerche sui semiconduttori e ad altre ancora.

2. Magnetismo. - La meccanica quantistica, assieme alle ricerche sperimentali a basse temperature ha avuto una considerevole influenza anche sullo studio del magnetismo nei solidi, in particolare nei cristalli ionici. Ci si rese conto che lo stato base degli ioni, assai lontano, nella scala energetica, dagli stati più alti, era fortemente influenzato dalla struttura cristallina. L'alto grado di simmetria riscontrato in molti cristalli rese necessaria l'applicazione di considerazioni sulla simmetria alla meccanica quantistica, per la quale si dimostrarono particolarmente adatti i metodi della teoria dei gruppi. Bethe, van Vleck e altri fecero vedere che i risultati di tali metodi potevano spiegare molte delle proprietà magnetiche osservate nei cristalli. Per determinare lo stato ionico di base furono necessarie misure a basse temperature, perché a temperatura ambiente andava presa in considerazione la media su vari stati quantici.

All'inizio si prestò meno attenzione alla suscettività magnetica dei composti ionici degli elementi metallici di transizione che alla suscettività elettrica di molte sostanze, ma la prima si dimostrò poi dal punto di vista atomico una sorgente di informazioni più ricca. Ciò divenne particolarmente evidente dopo la scoperta della risonanza paramagnetica degli elettroni, resa possibile dallo sviluppo delle tecniche radar e delle tecniche di microonde. Si trovò che la risonanza di spin elettronico (ESR, dall'inglese electron spin resonance) era strettamente legata alle misure di suscettività ad alta frequenza di cui Gorter aveva già dimostrato la grande utilità per lo studio della variazione temporale dei momenti magnetici.

Fu dimostrato che le vibrazioni del reticolo hanno una forte influenza sul cosiddetto ‛tempo di rilassamento spinreticolo', τ, cioè sul tempo medio durante il quale un momento magnetico ionico mantiene il suo orientamento rispetto a un asse fisso del cristallo o a un campo magnetico esterno. Si scoprì pure che a basse temperature il tempo di rilassamento diventa relativamente lungo (10^-6 − 10°s) rispetto al tempo di precessione (1'^-9 − 10^-8s) dei momenti magnetici elettronici intorno all'asse di un campo magnetico. Questi ultimi non sono più in grado di seguire variazioni rapide del campo, come per esempio quelle provenienti da un campo magnetico sovrapposto a radiofrequenza. A temperature alte, d'altra parte, il tempo di rilassamento può diventare più breve del tempo di precessione, eliminando l'effetto della risonanza di spin degli elettroni. In altri termini, l'energia degli stati quantici di uno ione magnetico in un campo magnetico non può più essere definita, in virtù della relazione quantistica di indeterminazione dell'energia.

Questa difficoltà non era invece così evidente nel metodo della risonanza magnetica nucleare (NMR, dall'inglese nuclear magnetic resonance), scoperto di lì a poco. Infatti, i momenti nucleari, essendo circa mille volte più piccoli dei momenti magnetici elettronici, sono molto meno influenzati dalle vibrazioni del reticolo. Perciò, l'uso delle basse temperature è molto più comune in ESR che in NMR.

I metodi di risonanza si basano essenzialmente sui cambiamenti di orientazione dei momenti magnetici fissi. Kip e Kittel scoprirono, quasi per caso, che gli elettroni nei metalli sono suscettibili di un tipo di comportamento di risonanza assai diverso. Se si applica a un metallo un campo magnetico statico e se perpendicolare a questo è allo stesso tempo presente anche un campo a radiofrequenza, si osserva una risonanza quando la frequenza del campo alternato è uguale alla frequenza di rivoluzione orbitale degli elettroni lungo l'orbita circolare (frequenza di ciclotrone) attorno al campo statico esterno. Questo moto è prodotto dall'applicazione del campo statico e tende a trattenere il campo magnetico fuori dal metallo, ed è quindi legato al comportamento diamagnetico dei metalli.

La risonanza di ciclotrone è da allora diventata uno strumento assai efficace per lo studio delle proprietà elettroniche dei metalli. Per tale studio è essenziale che le orbite circolari non siano interrotte dagli urti di elettroni tra loro o con atomi di impurità; per questo, sono necessarie basse temperature e metalli puri.

Ciò si verifica anche in un caso simile, cioè nell'effetto ‛de Haas-van Alphen', che consiste in un comportamento oscillatorio della suscettività magnetica degli elettroni di conduzione in funzione del campo magnetico esterno. Esso è collegato alla previsione fatta da L. D. Landau secondo la quale, per la teoria quantistica, i moti circolari degli elettroni devono avvenire su orbite quantizzate, il che è molto simile a certi fenomeni che si hanno in superconduttività e alla quantizzazione di Bohr delle orbite degli elettroni negli atomi.

Ritornando ai solidi ionici, si deve ancora notare che i momenti magnetici nei solidi sono relativamente piccoli e che soltanto facendo uso di temperature molto basse ci si può avvicinare al campo di saturazione, come fu mostrato per la prima volta da Kamerlingh Onnes per il solfato di gadolinio.

Il comportamento dei momenti elettrici nei solidi e nei liquidi era già stato studiato, in particolare da Debye e Onsager, i quali avevano mostrato che per poter dar ragione delle suscettività elettriche di vari materiali andavano prese in considerazione le interazioni tra momenti di dipolo. P.E. Weiss si era reso conto che i momenti magnetici, nonostante la loro piccolezza, hanno interazioni reciproche molto forti, rappresentabili mediante un campo magnetico effettivo che, per esempio, nel ferro è di ≈10⁸Oe. In seguito, si trovò che l'origine di questi enormi campi risiedeva nell'interazione quantistica di scambio, introdotta da W. K. Heisenberg. Ciò dà origine a transizioni di fase magnetiche nei solidi in cui, al diminuire della temperatura, può essere raggiunto un certo punto critico T_c (detto temperatura di Curie o di Neel) al quale il materiale diventa rispettivamente ferromagnetico o antiferromagnetico. Per un ferromagnete ciò significa che si è formato, in assenza di campi esterni, un momento magnetico spontaneo corrispondente ad uno stato ordinato in cui tutti i momenti magnetici sono paralleli, cioè uno stato di bassa entropia e di bassa energia. Un antiferromagnete è invece caratterizzato da un reticolo ordinato di momenti magnetici alternativamente paralleli e antiparalleli rispetto a un asse del cristallo. A queste transizioni di fase corrispondono massimi pronunciati nei calori specifici. La descrizione matematica di tali fenomeni collettivi aveva per lungo tempo presentato delle difficoltà insormontabili, fino a quando nel 1941 Onsager compì un grande passo avanti risolvendo esattamente il problema matematico di una transizione di fase in ipotetici reticoli bidimensionali di momenti magnetici. Di recente, questo lavoro è stato esteso a cristalli tridimensionali e sono stati trovati vari modelli che concordano con i risultati sperimentali relativi a transizioni di fase magnetiche in cristalli reali. F. Bloch mostrò teoricamente che alle basse temperature sistemi di spins ordinati presentano il fenomeno della propagazione di onde, le cosiddette ‛onde di spin' e vari tipi di esperimenti, per esempio misure di capacità termica a temperature basse rispetto a T_c hanno dimostrato che onde di spin si propagano effettivamente in materiali ferromgnetici.

Lo studio del magnetismo nei cristalli ha tratto grandi vantaggio dall'applicazione delle tecniche nate dalla fisica nucleare. Ciò è vero in particolare per la diffrazione di neutroni da parte di momenti magnetici, una tecnica molto efficace per l'analisi di reticoli periodici antiferromagnetici di momenti magnetici nei cristalli. Mediante la diffusione di neutroni su cristalli si possono studiare anche fenomeni dinamici, come per esempio le onde di spin.

Inoltre, Mössbauer mostrò che la radiazione gamma può, sotto certe condizioni, essere diffusa o assorbita in maniera risonante dai nuclei di un reticolo cristallino. La probabilità di assorbimento cresce quando la temperatura diminuisce, perché a bassa temperatura i nuclei degli atomi di un reticolo cristallino partecipano in maniera più ‛collettiva' alle vibrazioni di questo e possono muoversi meno liberamente, riducendo così la perturbazione sul processo di risonanza. Poiché l'energia del nucleo che assorbe il raggio gamma può essere misurata con estrema precisione, questo metodo permette di determinare la grandezza dei campi magnetici interni nei cristalli.

c) Conclusione.

Nel XX secolo vi è stato uno sviluppo straordinario delle nostre conoscenze sulla struttura atomica dei solidi, che è stato influenzato in modo determinante dall'avvento della teoria quantistica. Molti problemi riguardanti il comportamento dei solidi, che apparivano di difficile soluzione prima dell'introduzione dell'equazione di Schroedinger, furono in seguito facilmente risolti. Nei vari stadi di questo sviluppo l'utilizzazione delle basse temperature è stata di importanza determinante. A parte i problemi generali della fisica della materia condensata, vi sono ancora delle questioni che sono rimaste esclusivamente nel campo della fisica delle basse temperature dal tempo in cui Kamerlingh Onnes e i suoi successori le rilevarono; tali sono la superconduttività e le proprietà particolari dell'elio liquido. Un'esposizione coerente di questi problemi sarebbe impensabile senza la previa conoscenza della statistica quantica. Queste conoscenze sono spesso state raggiunte attraverso un cammino tortuoso. Alcuni dei momenti più importanti di tale cammino sono stati illustrati nel capitolo precedente.

3. Elio quattro liquido e superfluidità.

a) Elio quattro liquido.

L'elio fu liquefatto per la prima volta nel 1908; stranamente, però, dovettero passare 16 anni perché si osservasse una transizione di grande importanza a 2,2 °K. Solo nel 1932, poi, McLennan si accorse dell'immediata e totale scomparsa delle bolle di ebollizione che avveniva quando la temperatura si abbassava al di sotto di questo punto. Tale fenomeno, che è ora normalmente osservato da qualsiasi sperimentatore che lavori con le basse temperature, dimostra come si stabilisca molto rapidamente nel liquido l'equilibrio termico che impedisce la formazione di bolle di vapore. Tale osservazione condusse in seguito all'importante concetto di superfluidità, che insieme con quello di superconduttività dimostra in modo evidente come la meccanica quantistica operi su scala macroscopica.

Il punto di ebollizione dell'elio alla pressione di 1 atmosfera si trova alla temperatura di 4,2 °K. Riducendo la pressione si possono ottenere temperature più basse: in questo modo però non si può solidificare il liquido, come è invece possibile per quasi tutte le altre sostanze. Quindi, la prima straordinaria caratteristica dell'elio risiede nel fatto che esso rimane liquido fino allo zero assoluto. Ciò si spiega con il fatto che le forze di attrazione tra le molecole non sono sufficienti per superare il moto di ‛punto zero' delle molecole nel liquido, predetto dalla teoria quantistica. Questo moto di punto zero è particolarmente evidente nel caso di molecole leggere. Il fatto di rimanere liquido allo zero assoluto è comune soltanto all' ⁴He e all'isotopo raro ⁸He; vi è, però, una grande differenza tra i due liquidi isotopici: nell' ⁴He, infatti, la transizione superfluida avviene a 2,2 °K, mentre - come è stato dimostrato solo di recente - una simile transizione si può osservare nell'³He a temperature inferiori a 0,002 ⁰K. Si deve comunque dire che la solidificazione di ambedue i tipi di elio può essere raggiunta ad alte pressioni (25 atm per l'⁴He e 29 per l'³He).

Keesom e i suoi collaboratori trovarono che il calore specifico dell'⁴He liquido ha un massimo molto pronunciato a 2,2 °K. A causa della forma della curva del calore specifico, alla temperatura di transizione è stato dato il nome di punto λ (v. fig. 4). L'⁴He liquido nella regione di temperatura al di sopra di questo punto si chiama elio I e in quelia al di sotto (cioè nella zona della superfiuidità) elio II. Le proprietà dell'elio I sono quelle di un normale liquido, sì che non è necessario trattarle qui. La fig. 5 rappresenta un grafico della pressione dell'elio in funzione della temperatura: in esso si possono vedere le diverse regioni e la situazione a pressioni leggermente più alte. Si vede qui come il punto λ si sposti verso temperature più basse se la pressione aumenta: si ottiene, invero, una linea λ che comincia al punto di transizione sulla linea della tensione di vapore e che ovviamente finisce sulla linea di fusione.

b) Il modello a due fluidi dell'elio II.

Le proprietà dell'elio II furono studiate approfonditamente alla fine degli anni trenta e negli anni quaranta da molti sperimentatori, tra i quali sono da ricordare Keesom, Allen e, in particolare, Kapica. I risultati di questi studi portarono alla formulazione del cosiddetto modello a due fluidi, che è legato ai nomi di F. e di H. London, di Tisza e di Landau. Cominceremo con la descrizione del modello, discuteremo poi gli esperimenti e la loro spiegazione alla luce di quello e, infine, tratteremo il fondamento su cui esso si basa.

Nel modello a due fluidi si considera il liquido come composto di due fluidi interpenetranti, ognuno dei quali possiede una sua propria massa effettiva, cioè porta il suo contributo alla densità ρ del liquido. Inoltre, a ciascuno dei due fluidi si attribuisce una velocità o quantità di moto distinta, il che significa che essi si possono muovere indipendentemente l'uno dall'altro e che possono perfino obbedire a leggi e a equazioni idrodinamiche diverse.

Uno dei fluidi viene chiamato ‛fluido normale', con densità ρ_n e velocità v_n e l'altro ‛superfiuido', con le corrispondenti quantità es e v_s. In formule, si ha:

ρ_n + ρ_s = ρ_s (1)

j = ρ_nv_n + ρ_sv_s (2)

dove j indica il flusso totale di massa per unità di superficie del liquido.

Le proprietà dei due fluidi sono assai diverse. Il fluido normale è ‛normale' nel senso che si comporta come un qualsiasi fluido viscoso; il flusso del superfluido, invece, è apparentemente privo di viscosità, cioè non converte la sua energia cinetica in calore. Esso si comporta, a tutti gli effetti pratici, come un fluido allo zero assoluto; di conseguenza, tutte le proprietà termiche dell'elio liquido, come il calore specifico e l'entropia, devono essere esclusivamente proprietà della sua parte normale.

ρ_n e ρ_s dipendono fortemente dalla temperatura: al punto λ il liquido è completamente normale, cioè: ρ_n/ρ = 1 e ρ_s/ρ = 0, allo zero assoluto ρ_s/ρ = 1 e ρ_n/ρ = 0. Il valore di ρ_n/ρ decresce rapidamente dal punto λ in giù; alla temperatura di 1 °K, per esempio, esso è uguale a 1/100 (v. fig. 6).

Infine, si deve supporre che il flusso del superfluido derivi da un potenziale, che sia cioè irrotazionale. Ciò significa che la velocità e l'accelerazione del superfiuido si possono ottenere come gradienti di un potenziale (in modo analogo a quel che si verifica per il campo elettrostatico). Tratteremo questo argomento più approfonditamente alla fine di questo capitolo.

Nel capitolo seguente vedremo come, con un analogo modello a due fluidi, si possano descrivere molte proprietà della superconduttività (v. cap. 4, È d).

c) Osservazioni spiegate dal modello.

1. L'esperimento di Andronikasvili. - Una pila di dischi molto ravvicinati è sospesa a un filo sottilissimo (v. fig. 7). Questo sistema agisce come un pendolo di torsione che ruota intorno a un asse coincidente con il filo di torsione. Il periodo di oscillazione dipende dal momento di inerzia del sistema, il quale, a sua volta, dipende dalla massa dei dischi. Immergendo la pila nell'elio liquido e osservando le oscillazioni, si nota che la quantità di elio trascinata dal sistema decresce al raffreddarsi del liquido dal punto λ in giù. La spiegazione è semplice: il superfluido non viscoso non viene trascinato e soltanto il fluido normale contribuisce al momento di inerzia. Questo esperimento permette di determinare ρ_n, anche se non con grande precisione.

Il comportamento non viscoso del superfluido gli permette di filtrare attraverso fori molto fini senza ostruirli, e perciò, al di sotto del punto λ, anche piccolissimi fori in un recipiente possono determinare enormi perdite e creare così gravi problemi allo sperimentatore.

2. Trasporto termico. - È anche facile spiegare l'alta conducibilità termica. Consideriamo un tubo pieno di liquido ai cui capi venga mantenuta in qualche modo una differenza di temperatura (v. fig. 8). Nei liquidi normali il calorc viene trasportato dall'estremità calda a quella fredda mediante collisioni tra molecole, in modo tale che non si verifica un flusso netto di molecole. Questo è un processo relativamente lento. Nell'elio II il calore viene trasportato soltanto dal fluido normale. Il trasporto di calore avviene attraverso il moto dell'intero fluido normale dall'estremità calda quella fredda, mentre il superfluido scorre nella direzioni opposta, cosicché non si ha complessivamente alcun trasporto di massa. Questo processo di tipo convettivo è molto più efficace della conduzione di calore per collisione; l'unico modo in cui può esservi attrito si deve alla viscosità del fluido normale che dà origine al ben noto attrito di Poiseuille lungo la superficie interna del tubo.

Bisogna notare a questo punto che il quadro precedente va modificato quando le velocità di flusso non sono molto basse; se questa condizione non è soddisfatta, si hanno nuovi tipi di attrito. In verità, per velocità più alte anche il modello a due fluidi dev'essere modificato e perde la sua semplicità, ma tale modifica non tocca in maniera apprezzabile la facilità con cui vi può essere conduzione del calore.

La quantità di calore (Ó) trasportata dal fluido normale attraverso l'unità di superficie per unità di tempo si può scrivere:

Ó = ρv_nST, (3)

dove S è l'entropia per unità di massa.

3. Effetto meccano-calorico ed effetto fontana. - Una polvere molto fine pressata in un tubo costituisce un metodo efficace per impedire il flusso del fluido normale (grazie all'attrito viscoso), pur permettendo ancora al superfluido di muoversi liberamente. Questo filtro semipermeabile viene detto normalmente ‛superfiltro'. Consideriamo ora due recipienti, ciascuno dei quali contenga una certa quantità di liquido, collegati da un superfiltro (v. fig. 9A). Non è affatto necessario che le due temperature all'equilibrio siano uguali poiché il superfiltro è anche un isolante termico. Facendo passare una quantità di Δm grammi di liquido da sinistra a destra attraverso il filtro, la quantità di superfluido si riduce a sinistra e cresce a destra, a patto, però, che l'intero apparato sia termicamente isolato. Ciò significa una concentrazione maggiore di fluido normale, e cioè una temperatura più elevata a sinistra e una concentrazione minore a destra cui corrisponde una temperatura più bassa. Per mantenere costanti le temperature si deve sottrarre calore a sinistra e aggiungerlo a destra (v. fig. 9B). La termodinamica elementare mostra che, per ogni unità di massa spostata, la quantità di calore coinvolta è uguale a

Q_m = ST. (4)

Questo effetto si chiama effetto meccano-calorico.

Il suo completamento è l'effetto termo-meccanico o effetto fontana (fig. 9C). Se i due recipienti dell'apparato considerato sono mantenuti a temperature leggermente diverse, il superfluido tende a fluire verso quello più caldo. L'equilibrio si ha solo se questa ‛pressione osmotica' è controbilanciata da una differenza di livello corrispondente a una differenza di pressione

Δρ = ρΔT (5)

Termodinamicamente ciò significa che, in condizioni di equilibrio, la differenza di potenziale chimico per unità di massa

è uguale a zero. L'effetto fontana può essere illustrato in modo spettacolare (v. fig. 9D): riscaldando il punto giusto con una lampada, si riesce a produrre una fontana con uno zampillo alto parecchie decine di centimetri.

L'assenza di resistività del flusso superfluido è stata dimostrata recentemente in modo molto convincente mediante esperimenti con delle correnti ‛persistenti'. A questo scopo è stato necessario mantenere il flusso del superfluido in una struttura simile a una spugna, analoga a quella usata precedentemente: nei normali tubi larghi la possibilità di formazione di vortici sembra essere, infatti, troppo grande. Ritorneremo a considerare questi vortici tra breve.

Quando il superfluido è accelerato, la condizione di equilibrio è data, anziché dall'annullarsi della differenza di potenziale chimico, dalla relazione

in accordo con l'irrotazionalità del superfluido. Come si vede dall'equazione precedente, il potenziale chimico svolge esattamente il ruolo di un potenziale di flusso.

4. La pellicola di elio. - La natura non viscosa del superfluido gli permette di salire lungo le pareti del contenitore al di sopra del livello del liquido. In questo modo un piccolo recipiente può essere svuotato completamente, come si vede nella fig. 10A, che mostra il gocciolamento del liquido dal fondo esterno. Nella figura 10B il flusso della pellicola di elio continua fino a raggiungere la parità tra il livello interno e quello esterno.

5. Il secondo suono. - Il modello a due fluidi prevedeva in particolare un effetto che fu osservato sperimentalmente solo in seguito (V. P. Peškov, 1944): a causa della presenza di due fluidi nell'elio II, non soltanto può aversi la propagazione delle onde sonore ordinarie, legate alle oscillazioni di pressione e di densità, ma può aversi anche un secondo tipo di propagazione delle onde. Questo ‛secondo suono' è caratterizzato dal moto oscillatorio relativo dei due fluidi e da un'oscillazione simultanea del rapporto tra le densità parziali. In un'onda di secondo suono la densità totale e la massa complessiva del liquido rimangono costanti (v. fig. 11). Come apparirà evidente, l'oscillazione di ρ_n/ρ_s corrisponde a un'oscillazione di temperatura. Di conseguenza per rivelare il secondo suono è necessario un termometro e non un microfono, perché quest'ultimo risponde soltanto a oscillazioni di pressione. Il secondo suono si è rivelato uno strumento molto utile per lo studio dell'elio II: in circostanze normali, infatti, esso è solo debolmente attenuato e quindi si possono costruire e utilizzare dei risonatori, come si fa di solito con il suono normale. La velocità è data da:

dove c indica il calore specifico (v. fig. 12). La misura della velocità del secondo suono permette la migliore determinazione del rapporto tra le densità: ρ_n/ρ (v. fig. 6), perché il calore specifico c può essere facilmente misurato e l'entropia S può essere calcolata direttamente da c (v. sopra, cap. 2, È a).

d) Il fondamento del modello a due fluidi.

I gas che consistono di molecole con un numero pari di particelle elementari, come per esempio il gas ⁴He, obbediscono alla cosiddetta statistica di Bose e Einstein. Una caratteristica di tali gas è che, al di sotto di una certa temperatura, una parte delle loro molecole si scosta dalla normale funzione di distribuzione su tutti i valori dell'energia e si ‛condensa' allo stato di energia zero. Continuando ad abbassare la temperatura, a un certo punto tutte le molecole si dispongono in questo stato di zero assoluto. Se riuscissimo a dimostrare che un sistema di molecole che interagiscono fortemente, come quelle dell'⁴He liquido, deve presentare questo tipo di condensazione, avremmo allora un'adeguata spiegazione teorica del modello a due fluidi. L'³He liquido, che ha un numero dispari di particelle per molecola e che obbedisce alla statistica di Fermi anziché a quella di Bose, non mostra invece alcun comportamento a due fluidi, almeno fino a qualche milligrado al di sopra dello zero assoluto. Ciò è una prova decisiva della condensazione di Bose nell'³He liquido e, anzi, proprio questo ragionamento fu all'origine della formulazione del modello a due fluidi. La transizione superfluida, che è stata di recente osservata nell'⁸He a temperature inferiori a 0,002 °K, viene interpretata mediante un meccanismo di ‛appaiamento' elettronico, molto simile a quello dei superconduttori. La transizione pertanto non contraddice quanto è stato detto più sopra, dal momento che coppie di fermioni obbediscono anch'esse alla statistica di Bose. Purtroppo, però, la presenza di forti interazioni in un liquido rende impossibile lo sviluppo di una teoria quantitativa completa che possa essere confrontata con i dati sperimentali.

L'impostazione di Landau (1941) si dimostrò più proficua. Si tratta di un punto di vista tipicamente quantistico: il liquido viene considerato come un sistema macroscopico caratterizzato dal suo stato quantico, piuttosto che come un insieme di molecole che interagiscono. Allo zero assoluto il liquido è nel suo stato fondamentale; esso si può muovere come un tutto unico e si comporta come un superfluido, come mostreremo tra breve. A temperature diverse da zero lo stato eccitato del liquido può essere immaginato come il liquido nel suo stato fondamentale in cui si propagano certe vibrazioni o onde. Analogamente ai fotoni della radiazione elettromagnetica, e in accordo con il dualismo della meccanica quantistica, si può anche parlare di ‛quasi particelle' o di ‛eccitazioni' che si muovono nel fluido di fondo.

Queste eccitazioni sono caratterizzate dalla relazione tra la loro energia e il loro momento. Il momento p è direttamente legato alla lunghezza d'onda in accordo con la relazione di de Broglie λ = h/p, dove h indica la costante di Planck. Nell'elio liquido vi sono essenzialmente due tipi di eccitazioni: in primo luogo quelle con lunghezze d'onda molto maggiori della distanza intermolecolare, dette ‛fononi', e poi quelle con lunghezze d'onda dello stesso ordine di grandezza di tale distanza, dette ‛rotoni'. In circostanze normali, eccitazioni con momenti (o lunghezze d'onda) intermedi sono molto rare; la fig. 13 dà una rappresentazione completa di queste eccitazioni.

I fononi sono essenzialmente delle onde sonore ad altissima frequenza con una relazione energia-momento:

ε = cp (8)

dove c è la velocità del suono.

Non vi è alcun nesso fra rotoni e rotazione, e l'origine di tale denominazione è dovuta soltanto a un'errata interpretazione di Landau. Essi sono presenti solo a temperature piuttosto lontane dallo zero assoluto (sopra 0,5 °K) e obbediscono alla relazione

dove p₀ e μ_r sono costanti appropriate e per Δ v. fig. 13.

In sintesi, si ha un superfluido di fondo in cui è presente un gas diluito di fononi e di rotoni. Il numero di eccitazioni, ovviamente, non è costante, ma dipende dalla temperatura. In vicinanza del punto λ il gas diventa talmente denso che le interazioni tra le eccitazioni cominciano ad assumere un ruolo preponderante e siamo così di nuovo nella situazione in cui è impossibile far ricorso alla statistica di Bose e Einstein. La presente teoria non ci permette quindi di spiegare adeguatamente il punto λ stesso.

Questo modello può forse apparire molto artificioso e non realistico, ma, studiando la diffusione da parte dell'elio liquido di neutroni lenti, si scopre che il risultato concorda esattamente con l'ipotesi che la diffusione di elettroni sia dovuta alla collisione con particelle dotate precisamente dello stesso momento e della stessa energia di cui si è detto sopra. La fig. 13 è invero basata sui risultati di questi esperimenti di diffusione.

Il fluido normale può ora essere interpretato nel seguente modo: il moto del gas di eccitazioni risulta avere un certo momento risultante; il rapporto fra tale momento e la velocità di deriva delle eccitazioni fornisce una massa per unità di volume che è identificabile con la densità normale ρ_n. È essenziale che la densità normale calcolata in questo modo risulti minore della densità totale del liquido, per potere tener conto della massa del superfluido. E ovvio che questa condizione può essere soddisfatta soltanto se il numero di eccitazioni è relativamente basso. R. P. Feynman ha mostrato che ciò si verifica soltanto nei sistemi di Bose e Einstein. In tal modo si ribadisce ancora il ruolo essenziale della statistica di Bose e Einstein.

La natura del superfluido di fondo è stata chiarita da Landau. L'attrito che si sviluppa nel flusso del superfluido indica che la sua energia cinetica viene trasformata in calore, e cioè in eccitazioni. Ciò, però, non è possibile al di sotto di una certa ‛velocità critica', poiché si calcola che, altrimenti, sarebbe necessaria una quantità di energia maggiore di quella effettivamente disponibile. La velocità critica per la creazione di rotoni si determina prendendo la pendenza minima della tangente alla curva della fig. 13. Il valore che così si ottiene per tale velocità critica è di circa 60 m/s. I fononi possono essere creati solo da un superfiuido che si muova a una velocità superiore a quella del suono (240 m/s). In effetti, negli esperimenti si trovano velocità critiche molto più basse, ma ciò non invalida l'idea essenziale. Torneremo su questo più avanti.

Il calore specifico e le altre proprietà termodinamiche del gas diluito di eccitazioni possono essere facilmente calcolati per mezzo delle ben note leggi della meccanica statistica, quando siano note le relazioni energia-momento delle quasi-particelle; viceversa, è possibile dedurre da essi queste relazioni e confrontarle con i dati sulla diffusione dei neutroni. Sotto questo aspetto, l'accordo tra teoria ed esperimento è perfettamente soddisfacente.

Il modello del gas di eccitazioni permette di applicare i metodi della teoria cinetica dei gas al calcolo delle proprietà di trasporto, come ad esempio la viscosità del liquido. La viscosità è legata al trasporto del momento, che in questo caso avviene mediante le collisioni tra eccitazioni. I calcoli, che sono assai complessi a causa della presenza di vari tipi di collisioni, furono eseguiti con successo da Landau e Chalatnikov. In modo molto approssimato le collisioni possono descriversi riferendosi a un cammino libero medio. Di grande interesse è il cammino libero medio dei fononi il quale, dal momento che le collisioni tra fononi hanno scarsissimo effetto, è determinato essenzialmente dalle collisioni con i rotoni. Poiché il numero di rotoni decresce esponenzialmente al decrescere della temperatura, il cammino libero medio diventa molto grande a temperature basse. Questo è in accordo con il rapido aumento della viscosità al decrescere della temperatura al di sotto di 1 °K, ed allo stesso modo si può comprendere, per esempio, la crescente attenuazione, nelle medesime condizioni, del secondo suono. A causa della rarità dei rotoni al disotto di 0,6 °K, il cammino libero medio diviene assai più grande delle dimensioni dei normali apparati sperimentali. In effetti, l'osservazione del secondo suono diviene allora praticamente impossibile perché non si ha un numero sufficiente di collisioni per provocare un moto collettivo delle eccitazioni. È opportuno osservare che il secondo suono può essere identificato con un'onda di densità nel gas di eccitazioni, se si trascura il ‛riflusso' del superfluido che è molto piccolo a temperature basse: v_s/v_n = −ρ_n/ρ_s per il secondo suono, cioè molto minore di 1/100 a temperature inferiori a 1 °K.

Si ottengono risultati molto interessanti da esperimenti in cui vengano sciolte nel liquido particelle esterne. A tale scopo si possono usare atomi di ³He che possono interagire solo con le eccitazioni e che di conseguenza si comportano per molti versi proprio come un nuovo tipo di eccitazione, anche se, ovviamente, il loro numero è indipendente dalla temperatura. Essi fanno aumentare la densità normale e fanno spostare la transizione λ verso temperature più basse. Inoltre, le collisioni dei fononi con i rotoni sono assai simili a quelle con le ‛eccitazioni' di ³He, di modo che il cammino libero medio dei fononi può essere sensibilmente ridotto. Così, aggiungendo ³He, il secondo suono può essere osservato a temperature molto più basse. Sono stati fatti degli studi assai interessanti che non possiamo trattare qui, mescolando le particelle di Fermi con quelle di Bose.

Il quadro delle eccitazioni che abbiamo delineato spiega la maggior parte delle proprietà del fluido normale e di conseguenza del comportamento termico dell'elio II liquido. Tuttavia, dovremo un po' approfondire l'esame delle proprietà del superfluido per comprendere meglio, in particolare, il suo comportamento idrodinamico.

e) Gli aspetti quantomeccanici del superfluido.

Dal punto di vista della meccanica quantistica, una particella che si muove con velocità costante in una direzione x può essere descritta da una funzione d'onda complessa

dove A indica l'ampiezza, λ la lunghezza d'onda di de Broglie e ν la frequenza. L'espressione

si chiama fase dell'onda. È opportuno confrontare la (10) con un'onda reale quale si presenta, per esempio, in ottica:

Il significato fisico di ϕϕ* è la probabilità di trovare la particella nel punto x al tempo t; ψ* è il complesso coniugato di ψ, cioè il numero complesso che si ottiene sostituendo i con −i nell'espressione (10) di ψ. Poiché il prodotto dei fattori esponenziali di ψ e ψ* è uguale a 1, questa probabilità è indipendente dalla fase e risulta uguale ad AA* (o ad A² se A è reale). Di solito la fase non presenta grande interesse, ma faremo vedere che nel nostro caso, invece, essa è molto importante.

Come si sa, la lunghezza d'onda di de Broglie è legata al momento mv della particella dalla relazione λ h/mv, in cui h indica la costante di Planck. Sostituendo tale valore di λ nella (10a) si ottiene:

da cui segue che si può trovare v derivando la fase rispetto a x, o, più in generale, rispetto alla coordinata della direzione di propagazione, cioè prendendo il gradiente:

Inoltre risulta:

La funzione d'onda che descrive il moto dell'elio superfluido, cioè di un gran numero di particelle che si muovono quasi tutte con la stessa velocità, è soltanto una forma lievemente generalizzata dell'onda di una particella. Le relazioni (12) e (13) valgono ancora, con m che rappresenta la massa dell'atomo di elio e v la velocità del superfluido v_s; ψψ* viene ora interpretato come la densità locale del liquido. È essenziale rendersi conto che si suppone che tutte le particelle siano in un unico stato quantico macroscopico.

È inoltre importante ricordare che la fase è una variabile angolare, il che significa che se ϕ aumenta di 2π radianti, la parte esponenziale della funzione d'onda riprende il suo valore originale, proprio come accade per il fattore cosϕ in un'onda ottica reale.

È utile disegnare piani di uguale fase nello spazio contenente il superfluido; le linee di flusso del fluido sono perpendicolari a questi piani (v. fig. 14). Immaginiamo ora un cammino arbitrario da un punto 1 a un punto 2 nello spazio, dividiamolo in piccoli intervalli, e moltiplichiamo ogni intervallo per la componente di v_s, lungo esso. Con semplici passaggi matematici si vede che la loro somma dà:

È chiaro che facendo coincidere i punti 1 e 2, cioè compiendo un ciclo chiuso, si otterrà:

§ v_s • dl = 0. (15)

L'integrale che compare al primo membro dell'uguaglianza precedente si chiama circuitazione di v_s. Il rotore di v_s in un punto determinato viene definito come il limite del rapporto tra la circuitazione e l'area racchiusa dal ciclo, quando il ciclo tende a contrarsi riducendosi al punto considerato. Il risultato è che in ogni punto si ha:

rot v_s = 0. (16)

Questa relazione esprime, come già abbiamo visto in precedenza, una delle proprietà essenziali del superfluido, di cui ora abbiamo dato la dimostrazione.

Tuttavia la circuitazione sarà nulla soltanto se il cammino può essere scelto in modo tale che ogni piano di fase costante attraversato all'andata lo sia anche al ritorno. In uno spazio connesso come quello della fig. 14 questo è sempre possibile, ma ciò non si verifica se, come nella fig. 15, vi sono dei buchi nel liquido (caso di uno spazio molteplicemente connesso). Se si fa un giro attorno al buco, la fase lungo il percorso o cresce continuamente oppure decresce continuamente, e quindi il valore di quando si ritorna al punto iniziale non può più essere quello di partenza. D'altra parte, la funzione d'onda ha in ogni punto un unico e ben determinato valore. Entrambe le condizioni possono però essere conciliate, grazie alla dipendenza periodica della funzione d'onda dalla sua fase, se e solo se il cambiamento di fase che si ha girando intorno al buco è un multiplo di 2π. Di conseguenza la relazione (14) dà in generale:

con n intero, incluso lo zero. Bisogna notare che attorno a ogni punto nel liquido è effettivamente possibile scegliere un cammino con circuitazione uguale a zero e che lo si può contrarre a quel punto in modo che non sia mai violata la condizione che il rotore sia nullo.

f) Linee vorticose quantizzate.

I risultati del capitolo precedente hanno delle interessanti conseguenze per il semplice esperimento che segue (v. fig. 16). Un cilindro circolare (secchio) riempito in parte di elio liquido viene messo in rotazione a una temperatura superiore al punto di transizione. Dopo un breve tempo il liquido ruoterà come un corpo solido (v. fig. 16A) con la stessa velocità angolare del secchio. Durante la rotazione la temperatura viene abbassata, diciamo, a 1 °K, il che significa che in pratica l'intero liquido è diventato superfluido. Tuttavia una rotazione rigida non è irrotazionale, come si può facilmente verificare calcolando la circuitazione lungo un cammino circolare con centro sull'asse del cilindro. In base ai risultati del paragrafo precedente, questa rotazione rigida dovrebbe essere proibita. Una soluzione potrebbe essere che, passando attraverso il punto λ, si creasse un buco lungo l'asse e che, allo stesso tempo, il moto del fluido variasse in modo che la velocità tangenziale divenisse inversamente proporzionale alla distanza dall'asse; in altre parole, che la rotazione rigida si trasformasse in un unico grande vortice (v. fig. 16B). In realtà, apparentemente non accade nulla; nonostante la teoria, la rotazione rigida sembra persistere.

La soluzione di questo dilemma è relativamente semplice: invece di un solo grande vortice che implicherebbe un grande dispendio di energia, si formano molte linee vorticose parallele all'asse con buchi così piccoli da non essere rilevabili (v. fig. 16C). In questo modo, la rotazione media può ancora essere quella di un corpo rigido, ma le linee vorticose fanno sì che il rotore si annulli, come prevede la teoria. La circuitazione intorno a ogni vortice deve essere quantizzata, e si trova normalmente che il numero quantico è 1, cioè

Questo schema è ora generalmente accettato, anche se è assai difficile dimostrarlo rigorosamente. Tuttavia, vi sono indicazioni indirette sia dell'esistenza delle linee vorticose sia della quantizzazione della circuitazione. Tali linee vorticose dovrebbero muoversi, secondo l'idrodinamica, essenzialmente seguendo il moto medio del superfluido e - poiché ci si può aspettare che esse interagiscano con le normali eccitazioni - ci si deve anche attendere una specie di mutuo attrito in funzione della velocità del fluido normale rispetto al superfluido. Il modo migliore di studiare questo mutuo attrito è quello di cercare l'attenuazione del secondo suono, e gli esperimenti ne hanno dato un'elegante dimostrazione: 1) si è verificato che l'attenuazione del suono, propagantesi perpendicolarmente alle linee, è proporzionale al numero di linee calcolato (cioè proporzionale alla velocità di rotazione); 2) l'attenuazione del secondo suono, propagantesi lungo l'asse di rotazione, risulta invece molto debole, come era da aspettarsi visto che il moto delle eccitazioni lungo le linee è pochissimo ostacolato.

Questi esperimenti non costituiscono ancora una verifica del teorema di quantizzazione, poiché finora non è stato possibile effettuare un calcolo esatto dell'interazione tra eccitazioni e vortici.

Un esperimento molto ingegnoso fu compiuto da Vinen, e fu in seguito ripetuto da Zimmerman. In questa esperienza si dispone un filo sottile lungo l'asse di rotazione; ci si può così aspettare che lungo il filo abbia origine un'unica linea vorticosa, e quindi che attorno ad esso si crei una circuitazione. Studiando le vibrazioni del filo, la circuitazione può essere osservata e misurata in maniera assai diretta. In effetti, il risultato dell'esperimento fu positivo, anche se a causa delle instabilità sorsero varie complicazioni.

All'epoca in cui questo testo è stato scritto, sono stati pubblicati da Williams e Packards, di Berkeley, i primi risultati con immagini fotografiche delle linee vorticose.

La scoperta di tali linee vorticose ha anche risolto, in linea di principio, un problema annoso per quanto riguarda il flusso dell'elio II e cioè quello dell'esistenza di velocità critiche notevolmente inferiori a quelle previste da Landau e di complicati effetti di ‛attrito' che si riscontrano nelle correnti con velocità non troppo piccole. È del tutto ragionevole supporre che in qualsiasi flusso dei due fluidi si vengano a creare delle linee o degli anelli vorticosi, e che a causa del moto di questi, insieme al superfluido, si produca un mutuo attrito con le eccitazioni normali. La bassa velocità critica osservata potrebbe allora essere interpretata come la velocità a cui ha inizio la creazione di vortici. In effetti, già nel 1948 Gorter e Mellink introdussero un tipo di mutuo attrito proporzionale al cubo della velocità relativa, che bastava a giustificare tutta una serie di osservazioni sperimentali.

Si possono immaginare numerosi meccanismi per spiegare la creazione di vortici e la loro successiva crescita, ma essi non sono ancora stati studiati a fondo e molto resta ancora da spiegare dal punto di vista quantitativo. Tuttavia l'idea di una massa intricata di linee vorticose come modello di turbolenza del superfluido ha già ricevuto sufficiente dimostrazione. L'osservazione sperimentale che il flusso del superfluido possa essere turbolento mentre allo stesso tempo il fluido normale si comporta laminarmente è, dal punto di vista idrodinamico, un fatto assai strano.

Un fenomeno interessante, che potrebbe avere un'importanza pratica, è costituito dalla possibilità di ‛spazzare' le eccitazioni termiche per mezzo del flusso di un superfluido che porta dei vortici. La densità normale in un recipiente può essere in questo modo ridotta, il che significa che si può abbassare la temperatura. Così è stato osservato un effetto di raffreddamento di alcuni decimi di grado.

Non è possibile esaminare qui in dettaglio i numerosi studi che sono stati fatti sulla termoidrodinamica dell'elio liquido. Si può sperare che questi studi permetteranno alla fine di comprendere meglio la natura delle turbolenze anche nei liquidi normali, dal momento che in pratica solo nell'elio II è possibile separare la turbolenza dagli effetti viscosi.

Non è neppure possibile trattare qui a fondo un altro gruppo di esperimenti in cui viene studiato il moto degli ioni positivi e negativi nel liquido. Gran parte di queste ricerche furono compiute da Careri e dai suoi collaboratori a Padova e a Roma. Gli ioni sono particelle estranee, e di conseguenza si muovono essenzialmente con il fluido normale, ma d'altra parte si è visto che essi interagiscono fortemente con i vortici, offrendo così la possibilità di ottenere ulteriori informazioni sui vortici stessi.

Tratteremo ora uno di tali esperimenti che dà, forse, la migliore dimostrazione dell'esistenza di vortici e che fornisce anche una misura abbastanza diretta della circuitazione. I vortici o terminano sulla parete oppure sono chiusi su se stessi formando i cosiddetti anelli vorticosi. Gli ioni negativi hanno una forte tendenza a infiltrarsi nel buco di un vortice, il che significa che un anello in movimento può essere seguito mediante il rilevamento elettrico degli ioni. A temperature superiori a circa 1 °K questi anelli vengono perturbati dalle loro interazioni con i rotoni, mentre al di sotto di 0,5 °K essi sono molto più stabili perché i rotoni sono pochi e i fononi interagiscono solo in maniera trascurabile. Reif accelerò mediante un campo elettrico questi ioni attaccati a vortici e, avendone misurato la velocità, trovò che l'energia del sistema anello più ioni è inversamente proporzionale alla velocità ottenuta. Ciò è perfettamente in accordo con le previsioni dell'idrodinamica circa il moto degli anelli vorticosi. Il prodotto costante tra energia e velocità dipende solamente dalla circuitazione e dal raggio del buco del vortice. Poiché tale raggio può essere valutato con una discreta precisione, si può così calcolare anche la circuitazione e in effetti si trova il valore h/m previsto dalla teoria.

g) L'interferenza quantistica nell'elio liquido.

Consideriamo due recipienti pieni di elio liquido e collegati da un foro piccolissimo (10 μm: v. fig. 17A). Trascuriamo nel seguito il flusso del fluido normale e prendiamo in considerazione soltanto il superfluido. I recipienti devono essere abbastanza grandi, in modo che la velocità del superfluido sia apprezzabile soltanto nel foro e sia nulla in ogni altro punto. Allora, secondo l'equazione (11), le due funzioni d'onda nei recipienti possono essere scritte rispettivamente

ψ₁ = A₁ e 2^-πiν1t e ψ₂ = A₂^-2πiν2t

perché v_s può considerarsi nulla.

In generale le due fasi non sono uguali, anche se le due onde devono essere connesse attraverso il foro. Ciò significa che nel buco deve aversi un cambiamento di fase

ϕ₂ − ϕ₁ = 2π(ν₁ − ν₂)t

Questo slittamento di fase cresce in modo uniforme con il tempo e di conseguenza le due funzioni d'onda mostrano un'interferenza con una frequenza di battimento ν = ν₂ − ν₁. In altre parole, dopo un periodo di tempo uguale a 1/ν la differenza di fase è aumentata di 2π il che significa che entrambe le funzioni d'onda sono ritornate ai loro valori originari.

Per un cammino che passi attraverso il foro, in un dato istante, l'equazione (14) dà:

(v. fig. 17B) e, quindi, derivando rispetto al tempo:

Come conseguenza della natura irrotazionale di v_s, avevamo trovato, avvalendoci di considerazioni di termodinamica (v. sopra, cap. 3, È c, 3):

che può essere sostituita nell'equazione precedente. Alla fine otteniamo:

Concludiamo dunque che la frequenza dello slittamento di fase è direttamente proporzionale alla differenza di potenziale chimico e che di conseguenza essa è una grandezza osservabile. Bisogna ricordare che, invece, la frequenza della funzione d'onda stessa non è osservabile.

Fisicamente lo slittamento di fase ha origine perché nel foro si producono, a un ritmo appropriato, linee o anelli vorticosi. Consideriamo il cammino fisso della figura 17B. Se gli anelli vorticosi (‛anelli di fumo') si formano nel buco con un ritmo di ν anelli al secondo, il valore di ϕ₂ − ϕ₁ lungo il cammino cresce nel modo richiesto, perché ogni volta che un anello interseca il cammino, si ha un aumento nella fase di 2π. La figura illustra solo uno dei possibili rnodi di formazione dei vortici, ma anche configurazioni diverse possono portare allo stesso risultato.

Se i due recipienti sono alla stessa temperatura, μ₂ − μ₁ dipende soltanto dalla differenza di pressione, cioè dalla differenza di livello dei liquidi (Δz) nei due contenitori. Lo slittamento di fase è allora dato da

dove g è l'accelerazione di gravità.

La creazione di vortici nel modo indicato non è stata ancora sperimentalmente osservata; tuttavia è possibile indurre questi vortici per mezzo di una sorgente sonora di frequenza ν. Usando questo metodo di sincronizzazione, Richards e Anderson hanno osservato che la differenza di livello Δz tende a mantenere il valore corrispondente alla frequenza sonora, nel modo indicato sopra. A quanto sembra, la creazione di vortici riduce il flusso netto di superfluido attraverso il foro. Esperimenti successivi (Khorana) hanno dimostrato che, con una sufficiente energia sonora, il flusso può anche essere arrestato completamente; ciò significa che la differenza di pressione viene in qualche modo bilanciata da vortici che vengono prodotti al ritmo giusto. Naturalmente, il valore di v_s, nel foro deve oscillare simultaneamente con la stessa frequenza. L'esperimento può essere usato per una nuova determinazione del ‛quanto di circuitazione' h/m: basta misurare con sufficiente precisione la frequenza del suono e la differenza di livello.

Il fenomeno dello slittamento di fase che abbiamo qui delineato è analogo al cosiddetto effetto Josephson a corrente alternata tra superconduttori debolmente accoppiati, su cui ritorneremo in seguito (v. sotto, cap. 4, È 1).

Dall'epoca della prima stesura di questo testo sono state sollevate serie obiezioni sulla validità di questi esperimenti: pertanto, al presente (1974), non si è ancora dimostrata la possibilità di osservare l'analogo. dell'effetto Josephson nell'elio liquido.

4. La superconduttività.

a) Introduzione.

In un metallo ordinario la resistività elettrica decresce al decrescere della temperatura. Nella gamma di temperatura dell'elio liquido essa si avvicina a un valore costante, detto ‛resistività residua', che è determinato dalla purezza del campione (v. sopra, cap. 2, È b, 1).

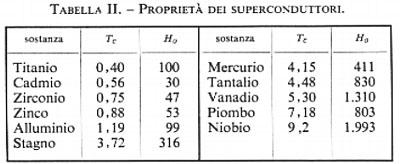
Nel 1911 Kamerlingh Onnes scoprì che il mercurio si comporta diversamente: infatti, a T = 4,2 °K la resistività scende improvvisamente a zero. Da allora lo stesso fenomeno è stato osservato anche in vari altri metalli, per ognuno dei quali la transizione avviene a una temperatura caratteristica, detta ora ‛temperatura di transizione', T_c. Questo fenomeno va sotto il nome di ‛superconduttività'. Alcuni esempi di superconduttività sono riportati nella tab. II. Fra tutti gli elementi, quello con la temperatura di transizione più alta è il niobio (9,2 °K), ma vi sono alcune leghe con temperature di transizione anche superiori a 20 °K.

La transizione è tanto più rapida quanto più pura è la sostanza. Per lo stagno purissimo essa avviene entro un millesimo di grado, mentre per campioni impuri la banda di transizione arriva fino a 0,1 gradi.

Se una corrente passa attraverso un superconduttore, a causa dell'assenza di resistenza non vi è diminuzione di tensione o riscaldamento per effetto Joule. Così nel campione non c'è alcun campo elettrico e tutte le affermazioni precedenti possono essere riassunte nell'equazione

E = 0. (21)

Quando un superconduttore a forma di anello è introdotto (o estratto) in un campo magnetico, in esso si genera una corrente indotta che, non subendo perdite di energia, continuerà per sempre (almeno finché la temperatura dell'anello sia mantenuta al di sotto di quella di transizione). Le correnti di questo tipo si chiamano ‛correnti persistenti': in alcuni esperimenti esse sono durate vari anni, senza alcuna diminuzione apprezzabile.

b) Il campo di perturbazione e l'effetto Meissner.

Immediatamente dopo la scoperta della superconduttività si pensò che potessero esser prodotti a basso costo dei campi magnetici di notevole intensità facendo passare una forte corrente in un solenoide superconduttore. Quest'idea si rivelò ben presto illusoria quando si scoprì che, nel caso del piombo, dello stagno, del mercurio e di altri metalli, la superconduttività viene distrutta da un campo magnetico anche relativamente debole. Questo cosiddetto ‛campo di perturbazione' H_c è nullo per T = T_c e cresce al diminuire della temperatura, avvicinandosi ad un valore H₀ per T = 0. Il grafico della funzione H_c(T) può essere approssimativamente rappresentato dalla parabola:

Alcuni valori di H₀ (in oersted) sono dati nella tab. II.

Oggi la superconduttività viene considerata come uno stato della materia, di modo che la curva di transizione (22) divide il diagramma H, T in due regioni: lo stato o fase ‛normale' al di sopra di esso, e quello ‛superconduttore' al di sotto (v. fig. 18).

In effetti, quando si instaura un campo magnetico (v. fig. 19), sulla superficie vengono indotte delle correnti persistenti che schermano dalla massa del campione il flusso magnetico (v. fig. 19B). Le correnti aumentano col crescere del campo magnetico, ma si estinguono improvvisamente quando viene raggiunto H_c, e così il flusso magnetico può penetrare nel campione (v. fig. 19C). Quando il campo scende di nuovo sotto H_c, il flusso magnetico viene a un tratto espulso e ricominciano le correnti persistenti. Quando il campo viene ridotto a zero, anche le correnti decrescono a zero.

Si possono riassumere le considerazioni precedenti affermando che, oltre che dalla (21), lo stato di superconduttore può essere descritto anche dalla relazione

B = 0, (23)

in cui B indica la densità del flusso magnetico, ossia l'induzione magnetica all'interno del campione. Questo fenomeno fu scoperto da Meissner e Ochsenfeld nel 1933, e ora l'espulsione del flusso da parte di un superconduttore viene detta ‛effetto Meissner'.

Ne illustriamo ora un'interessante applicazione. Consideriamo un cilindro superconduttore cavo a cui venga applicato un campo parallelo all'asse. A causa dell'espulsione del flusso da parte di questo materiale superconduttore, anche lo spazio all'interno del cilindro rimane privo di campo. Alla superficie esterna del cilindro si innescano, come sappiamo, delle correnti persistenti. Se il campo viene aumentato a un valore superiore a H_c, il flusso penetra sia nel superconduttore sia nella cavità interna del cilindro. Facendo nuovamente diminuire il campo al di sotto di H_c, il flusso nel superconduttore viene espulso mentre quello nella cavità vi resta intrappolato. Si stabiliscono così delle correnti persistenti in senso opposto sulla parete interna del cilindro. In generale si può dire che il flusso si conserva attraverso una cavità nel superconduttore.

L'immissione e l'espulsione del flusso magnetico a H_c, avvengono in maniera discontinua solo nel caso di un lungo campione cilindrico con l'asse parallelo alla direzione del campo. La cosa è più complicata, invece, se il campo viene posto perpendicolarmente all'asse o se si fa uso di un campione sferico. In tali casi, come è facile constatare dalla fig. 19B, l'intensità del campo vicino al campione diventa maggiore del campo medio a una distanza più grande. Per un cilindro perpendicolare, esso è due volte più grande, mentre nel caso di una sfera il rapporto è 3/2.

Se ora, al crescere del campo, si raggiunge il valore H_c ai lati del campione, lo stato superconduttore viene localmente perturbato di modo che il flusso può penetrare. Ma appena è penetrato, diciamo fino al punto b della fig. 20A, l'intensità del campo tra b e a diventa più piccola di H_c, cosicché lì il flusso deve di nuovo essere espulso. La configurazione stabile di flusso che viene finalmente raggiunta a questo punto, è quella illustrata nella figura 20B. Il campione è suddiviso in regioni sottili alternativamente normali e superconduttrici; il flusso magnetico passa attraverso le regioni normali, in cui H = H_c, mentre in quelle superconduttrici B = 0. Questa configurazione di flusso viene detta ‛stato intermedio'. La densità di flusso media su tutto il campione ha un valore compreso tra 0 e H_c. Più il campo esterno è vicino ad H_c, maggiore è la frazione normale del materiale e più alta è la densità di flusso media.

Nel caso di un campione cilindrico perpendicolare al campo esterno, lo stato intermedio si ottiene tra ½ H_c e H_c e, in quello di un campione sferico, tra ???16??? H_c, e H_c. Ciò concorda con il fatto sperimentalmente osservato che per un campione cilindrico parallelo al campo la resistenza elettrica è nulla per tutti i valori del campo inferiori ad H_c. Se il campo è disposto perpendicolarmente, la resistenza cresce gradualmente fra ½ H_c e H_c, mentre per una sfera essa cresce da ???16??? H_c, ad H_c Lo stato intermedio può essere sperimentalmente osservato in vari modi che dipendono tutti da una determinazione precisa dell'intensità del campo magnetico immediatamente fuori della superficie del campione. Lo spessore delle zone alternate normali e superconduttrici è dell'ordine di 0,1 mm.

c) Considerazioni termodinamiche.

La teoria dell'elettromagnetismo fornisce una relazione semplice tra l'intensità del campo magnetico H e l'induzione magnetica o densità di flusso B:

B = H + 4π M, (24)

dove M indica la magnetizzazione, o il momento magnetico per unità di volume del campione. Ciò significa che il metallo allo stato superconduttore (B = 0) ha una magnetizzazione M = −H/4π. Nello stato normale, trascurando piccoli effetti diamagnetici e paramagnetici, abbiamo che B = H, da cui segue M = 0. La curva di magnetizzazione, che nel caso di un materiale superconduttore è normalmente data da un diagramma di −4πΜ in funzione di H, è rappresentata dalla fig. 21A per un lungo campione cilindrico parallelo al campo. L'energia di magnetizzazione in un campo H obbedisce all'equazione

e la differenza totale di energia tra campo nullo e stati normali è uguale a

Per un cilindro trasversale e per una sfera, in cui si deve tenere conto della presenza di uno stato intermedio, le curve sono date dalle figg. 21B e 21C. In tutti e tre questi casi la differenza totale di energia ha lo stesso valore (25b), uguale alle aree dei triangoli.

Nel cap. 4, È b, abbiamo fatto notare che per un lungo cilindro parallelo al campo (che è l'unico caso che discuteremo in seguito) la transizione tra lo stato normale e quello superconduttore è reversibile. Quando il campo magnetico supera H_c, il flusso penetra nel campione e quando esso scende al di sotto di H_c il flusso viene improvvisamente espulso. Ciò significa che la transizione può essere trattata con i metodi della termodinamica classica. Così sulla curva di transizione della fig. 18 il potenziale termodinamico G deve avere lo stesso valore in entrambi gli stati.

Anche se non entreremo nei dettagli, è interessante notare che questa semplice affermazione dà luogo a un certo numero di conseguenze importanti. Per prima cosa, ne consegue che la curva di transizione, anche se non è esattamente una parabola, deve tuttavia avere una tangente orizzontale per T = 0. Inoltre la transizione dallo stato superconduttore a quello normale è accompagnata da un calore di transizione (analogo al calore di evaporazione di un liquido), eccetto che per T = 0 e per T = T_c. Si può anche ricavare una facile espressione per il calore specifico di un metallo superconduttore.

Per un metallo normale (e così anche per un superconduttore in un campo molto maggiore di H_c) il calore specifico a basse temperature obbedisce alla relazione

c_n = βT³ + γT (26)

dove il primo termine è legato all'energia di vibrazione termica del reticolo cristallino (cioè ai fononi) e il secondo al moto degli elettroni di conduzione. Per un metallo superconduttore il calore specifico può essere espresso approssimativamente da

c_s = βT³ + αT³, (27)

dove il primo termine è ancora legato all'energia di vibrazione termica e il secondo agli elettroni. In questo caso ambedue i termini sono proporzionali a T^a. L'equazione (27) può essere dedotta dalla (26) supponendo che la curva di transizione sia quella parabolica dell'equazione (22), il che porta alle relazioni:

Il calore specifico, sia nello stato superconduttore sia in quello normale, è illustrato nella fig. 22. La curva dello stato normale si ottiene compiendo gli esperimenti in un campo superiore ad H_c. La figura dimostra che durante la transizione a T_c il calore specifico a campo nullo scende rapidamente.

Esperimenti più recenti eseguiti con maggior precisione hanno dimostrato che il calore specifico elettronico nello stato superconduttore non è esattamente proporzionale a T³ e che la discrepanza più pronunciata si ha a temperature più basse (T 〈 ⅓T_c). Qualche decennio fa era quasi impossibile compiere esperimenti precisi sulla maggior parte dei superconduttori in questa gamma di temperature. Solo recentemente si è potuto osservare che il calore specifico elettronico ha un andamento esponenziale:

Poiché l'equazione (27) è stata ottenuta dalla (26) facendo l'ipotesi di una curva di transizione parabolica, è chiaro che gli scostamenti dalla legge di proporzionalità a T³ per il calore specifico elettronico devono essere accompagnati da deviazioni dall'andamento parabolico della curva di transizione.

d) Il modello a due fluidi.

Il fatto che l'uso del modello a due fluidi abbia dato buoni risultati sia nello studio della superconduttività sia in quello dell'elio II suggerisce che esista una spiegazione comune ai due fenomeni che sarà messa in evidenza in questo capitolo. Gorter e Casimir impiegarono questo modello nel 1934 per cercare di spiegare la superconduttività, ancora prima che esso fosse proposto per l'elio liquido (Tisza, London, 1938). Essi postularono che in un metallo allo stato superconduttore fossero presenti due tipi diversi di elettroni di conduzione. Una parte degli elettroni, che possiamo indicare percentualmente con 1 − x, è ‛normale', cioè essi si comportano allo stesso modo degli elettroni in un metallo non superconduttore. La frazione x è invece costituita da elettroni superconduttori, che hanno entropia nulla e si trovano quindi in uno ‛stato ordinato'. La frazione x di elettroni superconduttori si riduce a zero per T = T_c e cresce al diminuire della temperatura fino a raggiungere il valore 1 per T = 0. E evidente l'analogia con le parti normali e superfluide dell'elio II (v. sopra, cap. 3, È b).

Nel 1934 non era possibile dare una rappresentazione dettagliata dello stato ordinato, ma furono tuttavia attribuite agli elettroni superconduttori due proprietà fondamentali. La prima era che durante il loro moto attraverso il reticolo cristallino essi non venissero diffusi dalle vibrazioni termiche (cioè dai fononi) e dai difetti del reticolo stesso. La seconda era che essi non potessero trasportare energia termica attraverso il metallo.

In questo modello il calore specifico elettronico di un superconduttore consiste di due termini: il calore specifico degli elettroni normali e l'energia di eccitazione occorrente per trasformare a ciascuna temperatura il necessario numero di elettroni superconduttori in elettroni normali. Gorter e Casimir dimostrarono che se la somma di questi due termini è proporzionale a T³ secondo la (27), allora x deve soddisfare l'equazione:

il cui grafico è rappresentato nella fig. 23. Essa dimostra che, appena la temperatura scende al di sotto del valore T_c il numero di elettoni superconduttori cresce rapidamente via via che la temperatura continua a diminuire, cosicché a circa 4 ½ T_c quasi tutti gli elettroni sono diventati superconduttori.

Da ciò deriva che le equazioni (22), (27) e (30) (v. figg. 18, 22 e 23) danno una descrizione fenomenologicamente coerente dello stato superconduttore. Poiché, tuttavia, negli esperimenti si riscontrano piccole deviazioni dalla (27), neanche le altre due equazioni possono essere del tutto esatte.

Il modello a due fluidi spiega in modo assai semplice alcuni fatti sperimentali. L'annullarsi della resistenza è conseguenza del moto libero degli elettroni superconduttori. Anche nel caso in cui il loro numero sia piccolo, a temperatura appena inferiore a T_c, essi danno luogo a un corto circuito rispetto agli elettroni normali.

Inoltre la conduttività termica di un metallo nello stato superconduttore è minore che in quello normale. Ciò è facilmente comprensibile perché, sebbene gli elettroni su- perconduttori possano muoversi con facilità attraverso il metallo, essi non possono trasportare calore. Così l'energia termica è trasportata soltanto dagli elettroni normali il cui numero è minore che nello stato normale.

Evidentemente la differenza di conduttività termica è tanto maggiore quanto più bassa è la temperatura, e ciò ha condotto alla realizzazione di un semplicissimo interruttore termico, che può essere inserito fra due corpi assegnati. Tale interruttore non è altro che un filo superconduttore, per esempio di piombo, che collega i due corpi. Il filo è circondato da un piccolo solenoide che può fornire un campo maggiore dell'H_c del filo. A T = 0,1 °K il rapporto tra la conduttività termica del piombo normale e quella del piombo superconduttore può facilmente essere dell'ordine di 1.000, cosicché, se il filo ha dimensioni adatte, il contatto termico tra i due corpi può essere stabilito rendendo normale il filo oppure può essere interrotto rendendo il filo superconduttore.

e) La teoria di London.

Se un corpo superconduttore viene posto in un campo magnetico inferiore ad H_c, l'induzione è schermata dalle correnti persistenti della superficie. È ovvio che queste correnti non possono propagarsi in uno strato di spessore zero perché da ciò deriverebbe una densità di corrente infinita. Se, d'altra parte, le correnti sono indotte in uno strato di spessore finito, allora una parte di induzione magnetica deve penetrare anche in questo strato. Ciò fu osservato per la prima volta da E. e H. London nel 1935.

Se un elettrone si muove in un campo elettrico in condizioni di resistenza nulla, esso possiede un'accelerazione costante dv/dt. Poiché la densità di corrente obbedisce alla relazione J = nev, dove n è il numero di elettroni per unità di volume e v la loro velocità media, si ottiene nel caso di un superconduttore:

Qui m è la massa dell'elettrone ed e la sua carica, mentre n_s designa solo il numero di elettroni superconduttori per unità di volume, cioè, secondo la (30):

Sostituendo la (31) in una delle equazioni di Maxwell, si ottiene

che, dopo alcuni passaggi, dà

dove

ed l è la distanza dalla superficie.

L'equazione (34) significa che, se alla superficie del superconduttore si produce una variazione della densità di flusso (∂B/∂t)₀, essa dà Origine a una variazione della densità di flusso all'interno che tende esponenzialmente a zero al crescere della distanza dalla superficie. Ciò evidentemente non concorda con i risultati di Meissner e Ochsenfeld che dai loro esperimenti (v. sopra, È b) trovarono che B stesso si annulla all'interno del superconduttore. Per questo motivo i fratelli London proposero di sostituire l'equazione (33), nel caso di un superconduttore, con

che porta a

Questa equazione significa che si ha una densità di flusso nulla in tutto il corpo, all'infuori di uno strato superficiale con uno spessore dell'ordine di λ, che diventa così la ‛profondità di penetrazione'. Sostituendo i valori Opportuni nella (35) si vede che per la maggior parte dei superconduttori questa profondità di penetrazione è dell'ordine di 10^-5 mm.

Con ulteriori Sostituzioni nella (36) si ottiene un'espressione per la densità di corrente alla superficie:

il che significa che la profondità di penetrazione delle correnti persistenti è uguale a quella dell'induzione magnetica. Questo è illustrato nella fig. 24, in cui il piano l = 0 separa il materiale superconduttore (l > 0) da quello non superconduttore (l 〈 0). Le correnti schermanti sono perpendicolari alla direzione del vettore di induzione magnetica.

Le equazioni (31) e (36) si chiamano ‛equazioni di London'. Esse rappresentano la formulazione matematica corretta di due fatti sperimentalmente osservati: la resistenza nulla e l'effetto Meissner. Tali equazioni sono valide sia nell'interno del superconduttore sia nel suo strato superficiale. È evidente che la (36) non è in contraddizione con la (33), ma che è solo più restrittiva.

La relazione di dipendenza della profondità di penetrazione dalla temperatura è determinata, secondo la (35), dalla dipendenza di n_s (densità degli elettroni superconduttori) dalla temperatura. Considerando la (32) e la (30), si ottiene:

in cui λ₀ indica la profondità di penetrazione allo zero assoluto. La funzione λ (T) indicata dalla (39) è riportata nella fig. 25. La profondità di penetrazione è pressoché costante per le temperature più basse, ma aumenta fortemente vicino a T_c.

L'esistenza dell'effetto di penetrazione di London non influenza in maniera significativa gli esperimenti con corpi di dimensioni normali, ma può avere un ruolo importante quando si tratta di corpi molto piccoli. Nel caso di un foglio, diciamo di 1 mm di spessore, parallelo al campo, la maggior parte del metallo è ancora priva di flusso (v. fig. 26A); se lo spessore è dell'ordine di 10^-8 mm, l'intensità di B nel piano di mezzeria del foglio non è molto minore di quella che si ha all'esterno del foglio (v. fig. 26B). Allo stesso modo, se si considera un cilindro cavo la cui parete sia molto più spessa di λ, il campo all'interno della cavità è nullo (v. fig. 26C); se lo spessore della parete è, invece, dell'ordine di λ, il campo all'interno della cavità è minore di quello esterno, ma certamente non è nullo (v. fig. 26D).

Se all'interno di un corpo (fig. 26B) l'intensità dell'induzione B non è molto minore del valore del campo all'esterno, secondo l'equazione (24), −M deve essere notevolmente più piccolo di H/4π, e di conseguenza l'energia di magnetizzazione deve essere sensibilmente minore di −H²/8π, che è il valore dato dalla relazione (25a). Poiché la differenza totale di energia tra il campo nullo e gli stati normali si mantiene pari a H²_c8π (v. equazione 25b), ne segue che il campo di perturbazione per corpi molto sottili deve essere sensibilmente più intenso di quello per corpi di grandezza usuale. Questo effetto, invero, è stato confermato sperimentalmente.

f) La lunghezza di coerenza.

La teoria dei London, di cui abbiamo appena parlato, dà origine a un nuovo problema, come fece notare lo stesso H. London. A prima vista sembra che lo stato superconduttore, anche nel caso di un lungo cilindro parallelo ad un campo magnetico di intensità inferiore ad H_c, non sia lo stato a energia più bassa. Il ragionamento è il seguente.

Supponiamo che il superconduttore sia suddiviso in regioni sottilissime di materiale alternativamente normale e superconduttore, proprio come nello stato intermedio, eccetto per il fatto che le regioni sono molto più sottili, anzi, anche più sottili della profondità di penetrazione λ.

Nelle regioni normali il campo è uguale ad il H_c, il che dà origine a un'energia di campo magnetico di H_c²/8π per unità di volume. Negli strati superconduttori, a causa del fatto che essi sono assai più sottili di λ, l'induzione è quasi ugnale' ad H_c (v. fig. 26B) e da questo deriva un'energia di magnetizzazione molto bassa, come abbiamo fatto notare alla fine del paragrafo precedente. Ora, rendendo le regioni normali ancor più sottili di quelle superconduttrici, si può far diventare la loro energia di campo magnetico piccola a piacere. Così, mediante questa suddivisione, l'energia totale può essere resa più bassa di quella dello stato puramente superconduttore.

Avendo osservato che in effetti questa suddivisione non può aver luogo, London trasse la conclusione che essa deve essere ostacolata da un ulteriore contributo all'energia. London suggerì che una superficie di separazione tra una regione superconduttrice e una normale all'interno del metallo potesse in qualche modo dare origine a una quantità addizionale di energia per unità di superficie.

I dettagli di questo schema furono sviluppati da Pippard nel 1953. Seguendo il suo ragionamento, consideriamo una superficie di separazione nel metallo tra una regione normale e una superconduttrice. Nella regione normale la percentuale x di elettroni superconduttori è uguale a zero, mentre in quella superconduttrice x ha un valore finito determinato dall'equazione (30). Ora, Pippard fece notare che, sulla superficie di separazione, x non può variare improvvisamente da un valore all'altro e che per la transizione è necessaria una certa distanza ξ, detta ‛lunghezza di coerenza'.

Appena x differisce da zero in maniera sensibile, il materiale è essenzialmente superconduttore. Vi è un piccolo numero di elettroni superconduttori che dà origine a delle correnti persistenti che schermano dall'induzione magnetica la regione superconduttrice. La situazione è quella delineata nella fig. 27. Nella regione superconduttrice vi è uno strato, il cui spessore è dell'ordine di ξ, nel quale x varia da zero al valore di equilibrio (30). All'interno di questo strato ve ne è un altro in cui B varia da H₀ a zero. Esso tocca la regione normale e il suo spessore è dell'ordine di λ (per il momento abbiamo supposto λ > ξ).

In questo strato di spessore ξ il numero di elettroni superconduttori è così piccolo che troppi elettroni vengono eccitati dallo stato superconduttore a quello normale (v. sopra, È d). Da ciò ha origine un'energia addizionale di circa H_c²/8π per unità di volume o ξH_c²/8π per unità di area della superficie di separazione. D'altra parte, nello strato di spessore λ l'induzione magnetica è troppo elevata e l'energia di magnetizzazione è dunque troppo bassa (v. sopra, È e). Ciò dà origine a una diminuzione di energia di λΗ₀²/8π per unità di area, di modo che l'energia totale per unità di area è uguale a:

Questa è l'energia della parete, originariamente postulata da H. London, che impedisce al superconduttore di scindersi in moltissime regioni normali e superconduttrici e che stabilisce anche un limite superiore alla periodicità dello stato intermedio in casi come quello di un cilindro in un campo trasversale (v. sopra, È b).

Fin qui non abbiamo ancora fatto una stima della lunghezza di coerenza ξ. Ora, risulta che l'esistenza di ξ è una diretta conseguenza del principio di indeterminazione di Heisenberg:

ΔE • Δt = ℏ (41)

dove ℏ = h/2π e h è la costante di Planck. Se l'energia di eccitazione di un elettrone per la sua transizione da superconduttore a normale è circa k7T_c - e su questo punto torneremo in seguito - la corrispondente incertezza temporale è Δt = ℏ/T_c; se indichiamo con v_F la velocità degli elettroni di conduzione, detta ‛velocità di Fermi', allora l'incertezza di posizione è

Se questa è l'incertezza intrinseca nella posizione dell'elettrone, una variazione di x, ossia della densità di elettroni superconduttori, non può mai avvenire in una fascia più piccola di Δs, e così la lunghezza di coerenza è la seguente:

Se sostituiamo nella (42) i valori numerici appropriati, troviamo che, per lo stagno, il mercurio e il piombo, ξ è dell'ordine di 2 × 10^-4 mm, e quindi maggiore della profondità di penetrazione λ che è dell'ordine di λ mm (v. sopra, È e).

Da quanto precede si conclude che ξ è essenzialmente l'intervallo spaziale in cui la funzione d'onda ψ di un elettrone superconduttore è sensibilmente diversa da zero. Se tale intervallo è dell'ordine di 2 × 10^-4 mm, ossia di 2.000 distanze atomiche, le funzioni d'onda di numerosi elettroni si sovrappongono e si possono così verificare parecchie interazioni fra elettroni superconduttori.

Se x è la percentuale di elettroni superconduttori che si trovano in una certa regione dello spazio, allora x rappresenta anche la probabilità di trovare un elettrone superconduttore in tale regione. Così, secondo la meccanica quantistica, si ha:

x= ψψ* = ∣ψ∣², (43)

dove ψ* è il complesso coniugato di ψ. In relazione alla (43), x viene talvolta detto ‛parametro d'ordine.

g) Superconduttori di tipo II.

Le espressioni (35) e (42) per la profondità di penetrazione e la lunghezza di coerenza ξ non hanno alcun termine in comune. Non c'è dunque nessun motivo fondamentale per cui λ debba sempre essere minore di ξ, e infatti è stato osservato anche il caso contrario. I superconduttori con λ > ξ si dicono del I tipo, e il piombo, lo stagno e il mercurio ne sono esempi tipici (v. sopra, È f). I superconduttori con λ 〈ξ si dicono del II tipo, e ne sono esempi il niobio e molte leghe.

Secondo la relazione (40), l'energia della parete tra una regione normale e una superconduttrice è positiva per un superconduttore del I tipo, il che gli impedisce di scindersi in piccole regioni. Per un superconduttore del II tipo, invece, essa è negativa e così per queste sostanze è energeticamente favorevole suddividersi nel maggior numero possibile di regioni superconduttrici e normali.

La teoria dei superconduttori del II tipo è stata sviluppata principalmente dai quattro fisici sovietici Ginzburg, Landau, Abrikosov e Gorkov, per cui va di solito sotto il nome di ‛teoria GLAG'. In tale teoria si considera il rapporto:

detto ‛parametro di Landau-Ginzburg'. Si ha superconduttività del tipo quando x 〈 1 e del II tipo quando x > 1. Una teoria più rigorosa dimostra che l'effettiva transizione avviene a x = √-2.

È stato dimostrato che un miscuglio di regioni normali e superconduttrici non consiste di strisce parallele, bensì di sottili cilindri allo stato normale (detti ‛fasci di flusso') che formano un reticolo triangolare immerso in un ambiente allo stato superconduttore. La densità del reticolo cresce al crescere dell'intensità del campo. Questa configurazione si chiama ^tstato misto' e non va confusa con lo ‛stato intermedio' trattato nel paragrafo b. Quest'ultimo si riscontra anche nei superconduttori del tipo e dipende dalla forma del corpo. Lo stato misto, invece, si ha soltanto nei superconduttori del II tipo ed è indipendente dalla forma.

Secondo la meccanica quantistica, il flusso magnetico in un fascio di flusso è quantizzato e il relativo quanto di flusso Φ₀ dovrebbe essere uguale a h/e, dove h è la costante di Planck ed e la carica elettronica. Stranamente, però, il valore trovato sperimentalmente è minore di h/e per un fattore 2.

pari a 2×10^-7 gauss × cm².

La struttura di un fascio di flusso è illustrata nella fig. 28. Essa è abbastanza simile alla fig. 27, soltanto che ora risulta λ 〈 ξ. Lungo l'asse del fascio la percentuale x di elettroni superconduttori è nulla. Intorno ad esso, in una regione cilindrica di raggio dell'ordine di ξ (diciamo 10^-4 mm) questa percentuale cresce fino a un valore di equilibrio (30). La densità di flusso magnetico B lungo l'asse è pressoché uguale al campo H (non ad H_c) e in una regione di raggio dell'ordine di λ essa decresce fino a zero. Con un esperimento ingegnoso, Essmann e i suoi collaboratori riuscirono a rendere visibile il reticolo dei fasci di flusso.

Secondo la teoria GLAG, oltre ad H_c occorre introdurre per i superconduttori del II tipo due nuQvi campi di transizione, H_c1 e H_c2, detti rispettivamente campo critico inferiore e campo critico superiore. Per i campi esterni minori di H_c1 il comportamento è uguale a quello dei superconduttori del I tipo. Nel corpo non vi è così penetrazione di flusso: si ha un effetto Meissner completo e risulta B = 0 e −4πM = H. Quando H = H_c1, che nella teoria più semplice obbedisce alla relazione

(dove x è dato dalla 44), i primi quanti di flusso penetrano nel corpo. La densità di flusso del reticolo cresce al crescere del campo, cosicché il valore medio di B cresce mentre quello di −4πΜ diminuisce. Questo andamento continua fino a quando il campo esterno raggiunge il valore H_c2 che è determinato dalla relazione

H_c2 = H_cx√-2. (47)

La densità di flusso diviene così uguale a quella del campo esterno e da questo punto in poi il corpo si trova nello stato normale.

La curva di magnetizzazione, detta ‛curva di Abrikosov', è rappresentata nella fig. 29. Il campo H_c, detto ora ‛campo critico termodinamico', viene definito in modo tale che l'energia di magnetizzazione totale sia uguale ad Hc²/8π e le due aree tratteggiate nella figura sono quindi uguali. Sulla curva di magnetizzazione non appare alcunché di particolare in corrispondenza del valore H_c.

La fig. 30 mostra il diagramma di stato di un superconduttore del II tipo, che è analogo a quello della fig. 18. L'andamento di H_c1, come si vede dalla figura, è pressoché parabolico, mentre quello di H_c2 è quasi lineare in prossimità di T_c. La regione al di sotto della curva H_c1 rappresenta lo stato puramente superconduttore, quella compresa tra H_{c1 e} H_c2 rappresenta lo stato misto, mentre al di sopra di Hc2 si ha lo stato normale.

Nelle teorie più precise (per es. in quella di Maki) le formule (46) e (47) sono sostituite da espressioni più complicate. Il parametro x che compare in entrambe le formule viene sostituito da due parametri, che sono in generale diversi, ma che hanno lo stesso limite quando T tende a T_c.

In pratica, negli esperimenti si trovano raramente curve di magnetizzazione della forma di quella di Abrikosov (v. fig. 29), che si osservano soltanto nel caso di campioni purissimi. La ragione di ciò sta nel fatto che i fasci di flusso vengono facilmente ‛intrappolati' da impurità chimiche e fisiche (cioè da difetti del reticolo cristallino). Di conseguenza si formano nel corpo dei gradienti di densità di flusso che rendono troppo bassa la densità di flusso quando il campo è crescente (cosicché −4πM risulta troppo elevato) e troppo alta quando il campo è decrescente (cosicché −4πM è troppo basso). Questo fenomeno viene detto ‛fissaggio del flusso' (flux pinning) e porta alle curve di magnetizzazione del tipo illustrato nella fig. 31A. Si osservano allora fenomeni di isteresi e momenti residui, come nelle sostanze ferromagnetiche.

Accade talvolta, durante una variazione del campo, che un flusso intrappolato possa rimanere attaccato per un tempo abbastanza luogo ai centri di fissaggio fino a che improvvisamente si produce una valanga, detta ‛salto di flusso', nella quale può essere coinvolto un gran numero di quanti di flusso. Questo caso è illustrato nella figura 31B. In essa appare che un gran numero di quanti di flusso, intrappolati contemporaneamente in uno stesso centro di fissaggio, possono produrre un salto di flusso.

Recentemente sono stati compiuti molti studi sull'influenza della contaminazione chimica (magnetica e non magnetica), della tempera a freddo (che dà luogo a dislocazioni o a difetti di linea nel reticolo cristallino) e dell'irradiazione neutronica (che dà luogo a difetti puntuali) sull'irreversibilità della curva di magnetizzazione.

Si è così trovato che, in effetti, la superconduttività non scompare ancora del tutto al di sopra di H_c2. Se il campo è parallelo alla superficie del corpo e se questa è molto liscia, allora un sottile strato superficiale con uno spessore dell'ordine di ξ rimane allo stato superconduttore fino a un valore del campo H_c3 che, secondo De Gennes, dovrebbe essere uguale ad H_c2√-3.

Sono state prodotte delle leghe (per es. l'Nb₃Sn) per le quali il valore di H_c2 è elevatissimo e persino superiore a 100 kOe. Queste sostanze sono adatte alla costruzione di solenoidi ad alto campo magnetico, capaci di realizzare l'antica idea di Kamerlingh Onnes di cui abbiamo parlato nel paragrafo b.

h) Teoria microscopica della superconduttività.

Nei paragrafi precedenti abbiamo discusso alcune proprietà dei superconduttori senza entrare nei dettagli sulla vera natura dello stato superconduttore. Nel modello a due fluidi di Gorter e Casimir, il problema può formularsi semplicemente così: sotto quale aspetto gli elettroni ‛superconduttori' differiscono da quelli ‛normali'?

La soluzione di questo problema è stata data in un lavoro di Bardeen, Cooper e Schrieffer, per il quale ad essi fu conferito il premio Nobel nel 1972. La teoria, che dal nome degli autori è oggi generalmente indicata come teoria BCS, fu pubblicata nel 1957, quasi mezzo secolo dopo la scoperta della superconduttività. Un lasso di tempo così prolungato basta già a far intuire come la differenza fra gli elettroni superconduttori e quelli normali debba essere invero molto sottile.

Vari effetti sperimentali che abbiamo già trattato in precedenza forniscono indicazioni per la soluzione del problema. In primo luogo il quanto di flusso non è uguale a h/e, come ci si aspettava dalla teoria, ma ad h/2e (v. sopra, È g). Ciò fa pensare che nella superconduttività entrino in gioco delle coppie di elettroni piuttosto che degli elettroni singoli. Inoltre, l'andamento esponenziale del calore specifico elettronico (v. sopra, È c) indica che nella transizione di un elettrone dallo stato superconduttore a quello normale occorre un'energia di eccitazione. Se b nell'equazione (29) vale circa 1, tale energia è allora dell'ordine di kT_c. Ciò segue anche dall'esistenza della lunghezza di coerenza, cioè dell'intervallo in cui la funzione d'onda di un elettrone superconduttore è sensibilmente diversa da zero. Tale intervallo è dell'ordine di 10³ distanze atomiche (v. sopra, È f).

Un'altra indicazione per la soluzione del problema, di cui non abbiamo finora parlato, è il verificarsi dell'effetto isotopico. Studiando un isotopo di un dato elemento, che sia più pesante dell'elemento stesso, si trova che la temperatura di transizione T_c è leggermente più bassa nel caso dell'isotopo. L'effetto è piccolo, ma sembra che in vari metalli lo spostamento di T_c sia proporzionale a M^-1/2, dove M indica la massa atomica. Il fatto che gli atomi partecipino alle vibrazioni del reticolo in un modo che dipende dalle loro masse significa che le vibrazioni del reticolo cristallino, o più propriamente i fononi, hanno anch'esse un ruolo nella superconduttività.

Bardeen, Cooper e Schrieffer fecero notare che tra gli elettroni di conduzione di un metallo può sorgere un'interazione attrattiva, che può essere più intensa della repulsione elettrostatica (o di Coulomb). Ciò accade attraverso il reticolo cristallino. L'elettrone fa nascere una contrazione locale del reticolo degli ioni positivi a spese di una parte della sua energia e del suo momento. Viene così eccitato un fonone (cioè una vibrazione del reticolo) e si stabilisce temporaneamente un eccesso locale di carica positiva nella parte contratta del reticolo. Dopo che l'elettrone è passato oltre, tale carica positiva temporanea può attrarre un secondo elettrone la cui energia e il cui momento vengono anch'essi influenzati. L'attrazione indiretta fra i due elettroni che ne risulta dà origine a un'energia di legame e quindi a una diminuzione dell'energia totale della coppia.

Il verificarsi di tale interazione tra due elettroni di conduzione risulta più probabile se essi hanno spins opposti e quantità di moto (o momenti) opposte. Così, per la conservazione del momento, se prima dell'interazione i momenti dei due elettroni sono rispettivamente p e −p, dopo l'interazione essi saranno rispettivamente p′ e −p′. Se uno di questi ultimi due valori è già impegnato da un terzo elettrone del reticolo, allora, per il principio di Pauli, la transizione di ciascuno dei due elettroni è proibita. Dato che l'intervallo, in cui la funzione d'onda di un elettrone superconduttore è non nulla, è dell'ordine di ξ in tutte le direzioni, le funzioni d'onda di numerosi elettroni sono in parte sovrapposte cosicché vi sono sempre molti altri elettroni disponibili con uno dei quali un dato elettrone può formare una coppia e compiere una transizione.

Queste coppie di elettroni si chiamano ‛coppie di Cooper'. Il fatto che l'energia di una coppia sia minore di quella dei suoi componenti separati dà origine a un fenomeno importante. Lo spettro energetico del sistema elettronico mostra una zona proibita proprio in corrispondenza dell'energia di Fermi, cioè dell'energia di quegli elettroni effettivamente responsabili della conduzione elettrica (v. sopra, cap. 2, È b, I). Ne consegue che vi è un ‛intervallo energetico' la cui ampiezza si indica di solito con 2_ε0. Gli stati energetici, che in un metallo normale occupano la zona proibita, sono spostati o in su o in giù, producendo così una maggiore densità di stati immediatamente al di sopra e al di sotto dell'intervallo energetico. La situazione è quella illustrata dalla fig. 32.

Una teoria più precisa mostrerebbe che allo zero assoluto l'ampiezza dell'intervallo energetico soddisfa la relazione:

ε₀ = 3,5 kT_c, (48)

Qui tutti gli stati al di sotto dell'intervallo sono occupati e tutti quelli al di sopra sono vuoti (v. fig. 32A), il che significa che tutti gli elettroni sono appaiati.

A temperature finite un certo numero di queste coppie di elettroni è termicamente eccitato al di sopra dell'intervallo (v. fig. 32B) e ciò vuol dire che esse si scindono. La larghezza dell'intervallo di energia decresce al crescere della temperatura: quando quest'ultima è bassa essa è quasi costante, mentre in prossimità di T_c si restringe e in corrispondenza di T_c l'intervallo si chiude improvvisamente (v. fig. 33). Da questo punto in poi non si verifica più l'effetto di accoppiamento e il corpo si trova nello stato normale.

Sebbene l'esposizione che abbiamo fatto della teoria BCS sia assai concisa e di carattere qualitativo, essa permette tuttavia di comprendere meglio molti dei fenomeni precedentemente descritti. Ne passiamo in rassegna alcuni qui di seguito. Il fattore 2 del quanto di flusso (v. sopra, È g) è dovuto al fatto che vanno prese in considerazione le cariche di entrambi gli elettroni della coppia di Cooper. L'andamento esponenziale del calore specifico (v. sopra, È c) è dovuto all'energia finita 2ε₀ necessaria per scindere la coppia. La lunghezza di coerenza (v. sopra, È f) ha un ruolo essenziale perché, per la formazione di una coppia di Cooper, le funzioni d'onda degli elettroni devono in parte sovrapporsi. Diviene ora chiaro che nel modello a due fluidi (v. sopra, È d) gli elettroni supercondutton sono quelli appaiati, mentre quelli normali sono spaiati. Inoltre, si dimostra che è possibile ricavare direttamente l'equazione di London (36) dalla teoria BCS e spiegare così l'effetto Meissner (v. sopra, È e). L'effetto isotopico si verifica perché l'insieme degli elettroni del reticolo partecipa all'eccitazione fononica, la quale diventa tanto più probabile quanto più forte è l'interazione elettrone-fonone nel metallo, e quindi quanto più alta è la resistività a temperature elevate. Ciò conduce all'importante conclusione che i metalli che hanno bassa resistività a temperatura ambiente (come gli alcalini e i metalli nobili), a differenza di altri, non diventano superconduttori. La teoria BCS prevede per la resistenza anche il valore zero. Per quanto riguarda le correnti persistenti, osserviamo che se una corrente fluisce attraverso un corpo si ha una velocità (momento) comune di deriva del sistema degli elettroni di conduzione; per la conservazione della quantità di moto durante una transizione di una coppia, questa velocità di deriva non può mai andare perduta, e ciò spiega il verificarsi delle correnti persistenti.

Infine, l'affermazione che la quantizzazione del flusso è esattamente analoga alla quantizzazione della circuitazione dell'elio II è quasi ovvia (v. sopra, cap. 3, ÈÈ e ed f).

Si sarà notato che l'approfondimento della nostra conoscenza di questi fenomeni ha reso sempre più chiara l'analogia tra superconduttività e superfluidità. Tale analogia, venuta in luce con il modello a due fluidi, diventa molto stretta quando si confrontino le coppie di Cooper con gli atomi di elio superfluido, entrambi ‛condensati' in un unico stato quantico macroscopico, secondo il comportamento di particelle di Bose-Einstein.

i) Effetto tunnel.

Un'interessante conferma sperimentale dell'esistenza di un intervallo energetico è data dall'effetto tunnel'. Consideriamo una combinazione di due parti metalliche, che per ora supponiamo allo stato normale, separate da un sottilissimo strato isolante. Le figg. 34A e 34B illustrano due modi in cui ciò può farsi: nella prima una striscia di metallo è coperta da un sottile strato di ossido su cui viene fissata una seconda striscia. Nella fig. 34B si ha un arrangiamento più semplice: una punta metallica viene fortemente premuta contro un altro corpo metallico.

In pratica, lo strato isolante deve essere così sottile che la funzione d'onda di un elettrone che si trovi in una qualsiasi delle due componenti metalliche abbia ancora valori apprezzabili nell'altra componente, e ciò accade quando lo strato isolante è spesso circa 20 Å. Ciò equivale a dire che vi è una probabilità non nulla di osservare l'elettrone nella componente di metallo sbagliata. In altre parole, l'elettrone può filtrare attraverso l'isolante, cosicché applicando agli estremi della combinazione metallica una certa differenza di potenziale si osserva una debole corrente elettrica. In ciò consiste l'‛effetto tunnel' allo stato normale.

Se l'esperimento viene compiuto con due componenti di metallo superconduttore, i fenomeni diventano più complicati perché nessun elettrone di nessuna componente può passare per effetto tunnel a un livello energetico nella zona proibita dell'altra componente. Ciò è mostrato nella fig. 35 che rappresenta lo stesso diagramma della fig. 32B per due componenti di metallo superconduttore: esso e stato però ruotato di 90° di modo che gli assi dell'energia siano disposti verticalmente.

Nella fig. 35A non vi è differenza di potenziale tra i due metalli e le due energie di Fermi sono allo stesso livello. Nella fig. 35B la tensione (espressa per mezzo della differenza di energia eV) è minore dell'intervallo energetico. Il passaggio di elettroni per effetto tunnel dal metallo II al metallo I può avvenire soltanto negli intervalli energetici A e B perché soltanto in essi sono disponibili nel metallo I livelli energetici liberi. Nella fig. 35C, dove eV è uguale all'intervallo energetico 2ε₀, la situazione non è cambiata molto rispetto alla figura 35B. Invece, nella fig. 35D, dove eV è maggiore dell'intervallo energetico, il passaggio per effetto tunnel può anche aversi nell'intervallo energetico C. Così, appena eV supera la larghezza dell'intervallo energetico, la corrente cresce improvvisamente come è mostrato nella fig. 36: qui eV₁ è uguale all'intervallo energetico 2ε₀ e ciò fornisce un buon metodo per determinare sperimentalmente l'intervallo energetico.

Sono stati osservati degli importanti effetti tunnel anche tra due diversi superconduttori e tra un superconduttore e un metallo normale, ma essi non saranno qui trattati.

l) Effetti Josephson e interferenza quantistica.

Perfezionando il contatto tra due superconduttori, per esempio mediante uno strato isolante di circa lo Å di spessore, la correlazione tra coppie di Cooper da bande opposte rispetto alla parete isolante diviene apprezzabile e si ha così una situazione strettamente analoga a quella del passaggio del superfluido di elio II attraverso un foro piccolissimo (v. sopra, cap. 3, È g).

I fenomeni che si manifestano in tali condizioni si chiamano ‛effetti Josephson', dal nome dello scopritore della maggior parte di essi. Questi effetti sono stati studiati in modo più approfondito rispetto a quelli analoghi nell'elio liquido. Invero, nel caso della superconduttività, basta effettuare soltanto delle misure elettriche, che sono assai più semplici di quelle meccaniche necessarie nel caso dell'elio. Poiché recentemente sono state realizzate delle ‛giunzioni Josephson molto stabili e che si prestano alla produzione in serie, questi effetti portano ad applicazioni pratiche che sembrano assai promettenti, anche se sono ancora in fase di sviluppo (v. sotto, cap. 6).

Seguendo l'analogia con il caso del superfiuido, la differenza di potenziale chimico tra due recipienti pieni di elio liquido corrisponde, nel caso presente, alla differenza di potenziale elettrochimico. Quest'ultima si riduce a 2eV quando sia la pressione sia la temperatura hanno valori uguali da ambedue i lati della giunzione Josephson. Naturalmente 2e è la carica della coppia di Cooper e V è la normale differenza di potenziale. Inoltre, l'analogo del flusso di superfluido è la ‛supercorrente' i_s di elettroni superconduttori. In generale, si deve prendere in considerazione la supercorrente insieme alla corrente normale i_n, attraverso lo strato isolante, il che rende talvolta l'interpretazione dei fenomeni assai complicata.

Senza riprendere in considerazione le funzioni d'onda che intervengono nei fenomeni in esame, daremo solo i risultati in modo leggermente più completo di quanto è stato fatto per l'elio liquido.

Gli effetti Josephson possono essere riassunti dalle seguenti equazioni:

i_s = i₁ sen Δϕ* (49)

e

in cui Δϕ* è ancora la differenza di fase Δϕ = ϕ₁ − ϕ₂, cui però, nel caso del superconduttore, va aggiunto un termine dovuto alla presenza di un flusso magnetico:

dove Φ₀ è il quanto di flusso (v. sopra, È g). Il valore di i₁ è costante, ma dipende dall'intensità del legame.

Supponiamo in primo luogo che il campo magnetico sia assente. L'equazione (50) mostra che se V = 0, Δϕ* è una costante indipendente dal tempo e non necessariamente nulla. Di conseguenza, in accordo con l'equazione (49), una corrente non nulla può attraversare la giunzione anche se non è presente una differenza di potenziale. Il valore della corrente non può superare i₁. Questo fenomeno è detto ‛effetto di corrente continua'.

Se V è diverso da zero, ma costante, Δϕ* cresce linearmente con il tempo:

e quindi la supercorrente oscilla con la frequenza:

Questo cosiddetto ‛effetto di corrente alternata' è esattamente analogo a quello descritto dall'equazione (19) (v. sopra, cap. 3, È g) che può anche essere scritta:

dove x = h/m è il quanto di circuitazione.

Contrariamente a quanto si verifica nel caso dell'elio liquido - dove non è possibile osservare direttamente questo effetto di corrente alternata e bisogna fare ricorso al metodo di sincronizzazione (v. sopra, cap. 3, È g) - è invece relativamente facile osservare la frequenza della modulazione sovrapposta alla supercorrente. Poiché basta misurare soltanto una tensione e una frequenza, il valore di e/h si ottiene con una precisione di una parte su 10⁷; ciò conduce anche a una precisione mai prima raggiunta nella determinazione dell'importante costante di struttura iperfine 2πe²/hc della spettroscopia.

In pratica, la corrente misurata attraverso la giunzione contiene anche un contributo dovuto agli elettroni normali. La fig. 37 riporta come esempio la relazione tra tensione e corrente ottenuta sperimentalmente. È opportuno notare che nella figura sono riportati solo i valori mediati nel tempo e non le oscillazioni ad essi sovrapposte.

La presenza di un campo magnetico introduce il secondo termine nella differenza di fase generalizzata delle equazioni (51), (50) e (49). Dalla (51) si vede che, aumentando il flusso Φ di un quanto di flusso Φ₀ la fase cresce di 2π, e chiaramente ne risulta una dipendenza periodica dal campo magnetico. Inoltre, per il teorema della quantizzazione del flusso, il flusso totale, cioè la somma tra il flusso che ha origine dalla corrente e quello dovuto a un campo esterno, deve essere uguale a un numero intero di quanti di flusso. Il risultato finale è che la corrente massima i₁ varia periodicamente in funzione del campo esterno: essa è ugnale a zero se il flusso esterno attraverso l'area della giunzione (L d della fig. 34C) è esattamente uguale a un numero intero di quanti di flusso e raggiunge invece il suo valore massimo se il flusso esterno è esattamente uguale a (n + 1/2) Φ₀, con n intero.

La fig. 38A mostra la dipendenza di i₁ dal campo magnetico. Questo grafico è assai simile a quello che si ha per la diffrazione della luce attraverso una stretta fenditura. Invero, se due giunzioni Josephson sono collegate in parallelo si osservano dei fenomeni di interferenza simili a quelli che si verificano quando la luce passa attraverso due fenditure parallele. Poiché la superficie che contiene il flusso del campo è generalmente molto più grande di quella del singolo contatto, la figura di interferenza è molto più compressa (v. fig. 38B).

5. Temperature ultrabasse.

a) Metodi di raffreddamento.

Sebbene il raggiungimento delle temperature ultrabasse (〈 1 °K) non abbia rappresentato in se stesso un obiettivo, la motivazione di questa ‛ricerca dello zero assoluto' non fu, però, neppure costituita dalla possibilità di applicazioni tecnologiche. Si può dire, piuttosto, che almeno durante i primi settant'anni di questo secolo la discesa lungo la scala della temperatura (da 10 a 10^-6 gradi Kelvin) è stata motivata dal desiderio di studiare particolari fenomeni fisici. La scoperta di fenomeni inaspettati, quali la superconduttività e la superfluidità, ha spinto allo studio di vari campi della fisica a temperature molto basse. Prima di discutere alcuni di questi, torniamo alla scala della temperatura per vedere in che modo possano essere raggiunte tali basse temperature.

1. Demagnetizzazione adiabatica. - La liquefazione dell'elio permise a Kamerlingh Onnes di compiere esperimenti alla temperatura di circa 1 °K. Dopo di ciò furono necessari quasi trent'anni prima che fosse compiuto un altro importante passo avanti verso lo zero assoluto, quando, con gli esperimenti di demagnetizzazione adiabatica di Giauque (California) e di de Haas e Wiersma (Leida), si raggiunsero temperature nella regione dei centesimi di grado. Questo metodo si basa sulla polarizzazione dei momenti magnetici degli ioni nelle sostanze paramagnetiche alle temperature dell'elio liquido. Tale polarizzazione si ottiene applicando forti campi magnetici alla superficie di un campione della sostanza da raffreddare e quindi anche all'elio in cui esso è immerso. Di conseguenza sono necessarie elettrocalamite di notevoli dimensioni.

Supponiamo che il campo magnetico H venga applicato a ioni paramagnetici aventi un momento magnetico μ associato a un momento angolare di spin pari a 1/2. Allora la polarizzazione, che equivale alla magnetizzazione relativa, è

L'energia di magnetizzazione ∫H • dM, associata con l'allineamento degli spins lungo il campo, viene assorbita mediante scambio di calore con l'ambiente circostante, costituito di solito da una piccola quantità di gas He che si trova nel contenitore del campione (v. fig. 39). Questa fase del processo viene quindi indicata come stadio di magnetizzazione isotermica. Il passo successivo consiste nel pompar via il gas utilizzato per lo scambio di calore. Con ciò il campione resta termicamente isolato, purché il contatto termico con il suo contenitore, in assenza del gas, sia trascurabile.

In pratica ciò si può fare sostenendo il corpo, per esempio, con una bacchetta di vetro a pareti sottili o sospendendolo entro il contenitore con dei fili. Nella tecnologia delle basse temperature ha un'importanza assai rilevante il fatto che la conduttività termica di molte sostanze divenga bassissima a basse temperature. Ciò è dovuto all'assenza quasi totale, a queste temperature, di vibrazioni reticolari, cosicché la conduzione termica dipende dai gradi di libertà cinetici degli atomi dell'He gassoso o liquido, o, a temperature ancora minori, dal moto degli elettroni di conduzione nei metalli.

Dato che il corpo è ora termicamente isolato, lo stadio successivo, consistente in una drastica riduzione del campo magnetico dal suo valore iniziale H_i a un valore finale H_f, è un processo adiabatico o isoentropico. Ciò significa che tale processo si sviluppa in condizioni di entropia S costante, poiché

dove si è indicato con dQ il calore assorbito.

In altri termini, le popolazioni dei due sottolivelli Zeeman (v. fig. 40) non possono essere alterate da una riduzione del campo, per cui μH/kT rimane costante. La temperatura decresce quindi dal suo valore iniziale T_i a quello finale T_f proporzionalmente alla riduzione del campo, cioè

Per il valore T_f esiste un estremo inferiore che trae origine dai campi magnetici H_int che agiscono su ogni ione magnetico del corpo a causa della presenza degli ioni magnetici circostanti. Questa limitazione può, in teoria, essere superata impiegando un grande H_i, per esempio raddoppiando il campo: 2H_i (v. fig. 41A). Purtroppo con questo metodo, che richiede magneti molto più grandi, si ottengono temperature solo di poco più basse; è perciò più conveniente usare dei composti magnetici con campi interni H_int assai piccoli, come per esempio il nitrato di cerio magnesio (H_int ≈ 40 Oe). In pratica si possono così raggiungere temperature finali di 2-3 millikelvin che possono essere mantenute anche per varie ore.

2. Raffreddamento nucleare. - Gorter, e anche Kurti e Simon, suggerirono di utilizzare per la demagnetizzazione adiabatica il minuscolo momento magnetico dei nuclei atomici: il processo che ne derivò venne in seguito chiamato ‛raffreddamento nucleare'. Il vantaggio principale di questo procedimento dipende dalla piccola entità delle interazioni tra momenti magnetici nucleari, per cui i campi interni H_int sono soltanto dell'ordine di pochi Oe: è quindi evidente che si possono raggiungere temperature molto più basse (v. fig. 41B). Bisogna tuttavia superare enormi difficoltà per raggiungere una polarizzazione nucleare M apprezzabile. Poiché i momenti magnetici nucleari sono più piccoli di quelli elettronici per un fattore di circa 1.000, occorrono campi considerevolmente più grandi, mentre allo stesso tempo T_i dovrebbe essere piccola, conformemente all'equazione (54). Nel 1955 a Oxford furono ottenute temperature dell'ordine di qualche milionesimo di grado.

Nel 1970 Lounasmaa e i suoi collaboratori a Helsinki produssero il raffreddamento di un campione di rame di 1,5 kg che rimase al di sotto di 1 millikelvin per 5 ore. L'apparecchiatura sperimentale era montata su un blocco di cemento armato posto su molle per ridurre le vibrazioni, ed era collocata in un ambiente elettricamente schermato per impedire che le emissioni delle stazioni radio e TV scaldassero il campione. Inoltre, furono usate delle bobine superconduttrici per produrre il campo H_i, e un refrigeratore a diluizione (v. sotto, 3) per ottenere bassi valori di T_i. Usando una tecnica assai diversa per ottenere alti valori di polarizzazione nucleare, Abragam e i suoi collaboratori a Saclay dimostrarono che l'interazione nucleare tra nuclei di fluoro nel CaF₂ dà origine a una transizione di fase magnetica a una temperatura leggermente inferiore a 1 microgrado.

3. Raffreddamento con l'³He. - L'elio che si trova nelle sorgenti di gas naturale o nell'atmosfera contiene soltanto da 0,1 a 1 parte per milione dell'isotopo leggero ³He. Tuttavia la produzione postbellica di armi per l'arsenale nucleare ha fornito come sottoprodotto delle quantità di ³He che sono state messe a disposizione della ricerca scientifica. Le proprietà dell'³He, come vedremo nel cap. 5, È b, sono insolite ed estremamente interessanti. Grazie alla sua piccola massa e quindi all'elevata energia quantomeccanica di ‛punto zero', l'³He non solidifica a pressioni inferiori a 29 atmosfere. Esso liquefa a 3,2 °K e rimane allo stato liquido fino allo zero assoluto. Contrariamente all'⁴He, l'³He conserva una grande capacità termica anche a temperature assai basse. Diminuendo la pressione su un bagno di ⁸He liquido, l'evaporazione fa scendere la temperatura al di sotto di 0,3-0,4 gradi. A queste temperature, bastano pochi centimetri cubi di ³He liquido per poter assorbire una considerevole quantità di calore, ad esempio per raffreddare un corpo immerso nell'³He. L'energia assorbita viene estratta dal liquido aspirando con la pompa a vuoto quegli atomi, in numero relativamente piccolo, che hanno energia cinetica sufficiente per passare dallo stato liquido a quello di vapore (v. fig. 42A). A temperature molto basse il numero di questi atomi diviene bassissimo e perciò la velocità di estrazione del calore diventa troppo bassa e rende il processo inefficiente. Dato che gli scambi di calore sono inevitabili, non si possono quindi raggiungere, con un refrigeratore a evaporazione di ³He, temperature che siano sensibilmente più basse di 0,3 °K.

Lo studio di miscele di ³He e ⁴He liquidi ha portato a un sistema di raffreddamento più efficace, il cosiddetto refrigeratore a diluizione di ³He e ⁴He. Il criterio di funzionamento ditale refrigeratore assomiglia a quello dell'evaporatore a ³He (v. fig. 42B), ma invece di una fase liquida e una gassosa abbiamo ora due fasi liquide. Si trovò che a temperature basse le miscele di ³He e ⁴He si separano in due fasi, l'una ricca di ³He e l'altra ricca di ⁴He. Quest'ultima, detta ‛fase diluita', può essere paragonata alla fase di vapore di ³He nella fig. 42A, in cui lo spazio vuoto è riempito da atomi di ⁴He. La fase diluita può contenere fino al 6% di ³He anche allo zero assoluto, ma per il resto si comporta essenzialmente come un gas perfetto di atomi di ³He che si muovono in un ambiente inerte di ⁴He. Supponiamo di avere realizzato questa separazione di fase in un contenitore, o camera di miscelazione, raffreddandolo fino a una temperatura inferiore a 0,5 °K. La fase diluita, essendo più ricca di isotopo pesante, occupa la parte inferiore del contenitore che è collegato mediante un tubo a una pompa. La pompa estrae di preferenza dal liquido in evaporazione atomi di ³He perché quest'ultimo ha un punto di ebollizione più basso dell'⁴He. La concentrazione decrescente di ³He nella fase più bassa viene tuttavia riportata immediatamente al suo valore originale dagli atomi di ³He che passano attraverso la superficie di separazione tra le fasi. Inoltre, se l'³He viene condensato continuamente nella fase superiore mediante afflusso di gas da un serbatoio esterno, l'effetto risultante è semplicemente una circolazione di atomi di ³He. Più precisamente, il trasporto di massa è associato a un trasporto di calore nel verso che va dal contenitore freddo al serbatoio esterno caldo. Il punto più importante nel circuito percorso dagli atomi di ³He è l'ingresso nella fase diluita, per il quale è necessaria una certa quantità di energia. Ciò porta a un raffreddamento della camera di miscelazione fino a 5-10 millikelvin. La ricondensazione dell'³He mediante l'afflusso di gas dal serbatoio esterno a temperatura ambiente riscalderebbe immediatamente il liquido freddo, e perciò si fa in modo che tale condensazione avvenga in un condensatore separato, o camera di condensazione, raffreddato da un altro bagno di ⁴He in cui viene immerso l'intero apparato.

Il vantaggio principale del metodo di raffreddamento a diluizione consiste nel fatto che, anche a temperature di qualche millikelvin, nella fase inferiore è sempre presente una quantità costante di ³He, pari al 6%, per mantenere la circolazione; in ciò sta la differenza rispetto al metodo a evaporazione, dove l'³He disponibile diminuisce esponenzialmente con la temperatura. Tuttavia la velocità di trasferimento del calore decresce con la temperatura, cioè diminuisce il potere di raffreddamento, il che limita la temperatura a pochi millikelvin. Agli effetti pratici, il raffreddatore a diluizione ha il vantaggio di mantenere costante la temperatura, mentre con la demagnetizzazione adiabatica, per esempio, si ha un'immediata caduta della temperatura fino al suo valore più basso T_f, dopo di che è inevitabile un graduale riscaldamento.

b) Proprietà dell' ³He.

La disponibilità di ³He ha fornito ai fisici delle basse temperature l'occasione unica di studiare un liquido composto di atomi che, a causa del numero dispari di nucleoni del nucleo, hanno un momento angolare di spin semintero. Va osservato che gli atomi di elio, come quelli degli altri gas nobili, non si combinano in molecole. Le particelle con spin ½ ℏ obbediscono al principio di Pauli, secondo il quale i livelli energetici possono essere occupati al massimo da due particelle. Se due particelle di spin 1/2 occupano lo stesso stato, i loro momenti angolari di spin devono essere opposti. I sistemi costituiti da queste particelle obbediscono alla statistica di Fermi-Dirac, le cui predizioni si discostano molto, alle basse temperature, da quelle della statistica classica di Boltzmann. Le proprietà dei metalli, per esempio, assai diverse da quelle degli isolanti, possono essere spiegate dalla statistica di Fermi-Dirac applicata agli elettroni esterni degli atomi dei metalli, come fu messo in evidenza nel periodo tra il 1930 e il 1940. In particolare, la proporzionalità del calore specifico e della conduttività termica con la temperatura si spiega facilmente contando il numero di elettroni che sono liberi di muoversi. Tali elettroni si trovano in livelli di energia, che sono solo parzialmente occupati, intorno alla cosiddetta superficie di Fermi, costituendo così una regione sfumata che separa la regione dei livelli completamente occupati da quella dei livelli completamente liberi (v. fig. 43). Il numero dei livelli energetici e degli elettroni in tali livelli, in altre parole lo spessore della regione sfumata intorno alla superficie di Fermi, è proporzionale alla temperatura T finché questa si mantiene al di sotto di un valore caratteristico T_F detto ‛temperatura di Fermi'. Al di sopra di T_F la differenza tra la statistica di Fermi-Dirac e quella di Boltzmann diventa piccola. Nei metalli si ha sempre T ≪ T_F, poiché T_F è pari ad almeno 10.000 °K. Per gli atomi di ³He liquido si trova che T_F ≈ 0,4 °K. Il valore di T_F dell'³He può essere aumentato mediante compressione o, inversamente, può essere abbassato sciogliendo l'³He nell'⁴He liquido. In ogni caso si trova che la capacità termica dell'³He liquido è proporzionale alla temperatura fino a circa 2 millikelvin.

Le proprietà di conduttività dipendono non solo dal numero delle particelle in gioco, ma anche dai meccanismi di diffusione. Poiché la diffusione degli elettroni nei metalli a basse temperature è causata da impurità ed è indipendente dalla temperatura, sia la conduttività elettrica sia quella termica sono proporzionali a T. D'altra parte, il moto degli atomi di ³He nel liquido è ostacolato dalle collisioni con altri atomi di ³He.

Le proprietà di diffusione si spiegano tenendo conto degli stati energetici discreti occupati dalle particelle sia prima che dopo la diffusione, secondo il principio di Pauli. Di conseguenza, la diffusione - in cui deve essere conservata l'energia totale - avviene solo in prossimità della superficie di Fermi (v. fig. 44). A bassa temperatura ogni particella negli stati di bassa energia non può passare a stati di più alta energia non occupati: infatti, in tal caso, un'altra particella di ³He dovrebbe a sua volta passare a un livello di bassa energia non occupato, diverso da quello reso libero dalla prima particella. Quest'ultima condizione è legata al concetto quantistico, conseguenza del principio di Pauli, secondo cui lo scambio di due particelle identiche non è osservabile. Per particelle che si trovano in stati vicini alla superficie di Fermi la probabilità di trovare due livelli finali liberi è proporzionale al prodotto delle probabilità di trovare un livello libero per ognuna della particelle separatamente. Da questo segue che la probabilità di un urto è proporzionale a T², o, inversamente, che il tempo τ tra due diffusioni è uguale a l/T³. Ora, la conduttività termica K è data da:

dove v, cioè la velocità della particella, è praticamente indipendente da T. Inoltre, C, la capacità termica, è proporzionale a T, mentre λ, il cammino libero medio tra due collisioni, è legato a τ dalla relazione λ = vτ. Ne segue

La validità della (57) è stata verificata sperimentalmente. Al di sotto di 1 millikelvin la conduttività termica dell'³He dovrebbe essere superiore a quella del rame più puro. Con un ragionamento analogo a quello testé svolto per la conduttività termica, si deduce che la viscosità deve crescere al diminuire della temperatura come 1/T², e in effetti anche questo è stato verificato sperimentalmente. Quindi, in sorprendente contrasto con le proprietà superfiuide dell'elio quattro, l'³He alle basse temperature diventa un fluido estremamente viscoso: alla temperatura di 1 millikelvin, per esempio, esso è più viscoso dell'olio di oliva a temperatura ambiente.

È stata avanzata l'ipotesi che a temperature estremamente basse (T 〈 0,01 °K) gli atomi di ³He potrebbero appaiarsi in particelle a spin intero, dando luogo a fenomeni simili a quelli che si verificano nello stato superconduttore dei metalli, dovuto all'appaiamento degli elettroni di conduzione. La statistica di Fermi-Dirac dovrebbe essere allora sostituita da quella di Bose-Einstein e le proprietà dell'³He potrebbero diventare simili a quelle dell'⁴He liquido. Nel 1972 è stata osservata per l'³He sotto pressione una transizione di fase a circa 2,6 millikelvin accompagnata da un cambiamento drastico del magnetismo nucleare di spin. La transizione di fase può quindi essere associata alla formazione di coppie.

Tra il 1972 e il 1974 un gran lavoro sperimentale è stato compiuto dai gruppi di Wheatley (a La Jolla, negli S.U.A.), di Lee (alla Cornell University, negli S.U.A.), di Lounasmaa (a Helsinki, in Finlandia), per comprendere la natura e le proprietà di questa transizione. Si è dimostrato in via definitiva che l'³He può divenire superfluido: ciò avviene alla temperatura di 2,6•10^-3 °K, se si lavora alla pressione di liquefazione di 30 atm, e alla temperatura di 0,93•10^-30 °K alla pressione normale di 1 atm (Lounasmaa e collaboratori).

L'³He solido si ottiene esercitando sul liquido una pressione tale che il volume disponibile per gli atomi di ³He si riduca fino al punto in cui essi sono localizzati in posizioni pressoché fisse nel reticolo cristallino. Quando i singoli atomi di ³He sono così dislocati, essi diventano distinguibili e quindi non è più applicabile la statistica di Fermi-Dirac per particelle identiche (cioè non distinguibili) di spin semintero. Un'importante conseguenza di ciò è che nel solido gli spins non sono antiparalleli a coppie e quindi, a bassa temperatura, il solido ha un'entropia maggiore di quella del liquido, in contrasto con quanto si verifica per i liquidi usuali. A bassa temperatura l'entropia del solido è dovuta quasi esclusivamente al disordine degli spins.

Questo fatto è stato sfruttato in un metodo di raffreddamento suggerito da I. Ja. Pomerančuk. Supponiamo di comprimere una miscela di ³He liquido e ³He solido che si trovi già a temperatura assai bassa (0,2 °K): allora, il liquido si trasformerà in solido. Se la compressione può essere realizzata senza somministrazione di calore (cioè a entropia costante), la temperatura della miscela deve diminuire perché altrimenti aumenterebbe l'entropia. Con questo metodo sono state raggiunte temperature di pochi millikelvin.

Le proprietà di un liquido di particelle che obbediscono alla statistica di Fermi-Dirac sono state studiate a fondo dal punto di vista teorico, in particolare da Landau e Chalatnikov. Lo studio di questi ‛liquidi di Fermi' permette di chiarire le proprietà del plasma nucleare composto di nucleoni con momento angolare semintero. Esso si è dimostrato particolarmente importante per spiegare le peculiari proprietà delle stelle pulsanti, le cosiddette pulsar, che si suppone consistano quasi esclusivamente di neutroni. Per esempio, la perdita di energia di tali stelle è in tutto analoga a quella descritta dai meccanismi di conduttività termica nell'⁸He liquido e nell'³He solido. Inoltre, gli improvvisi cambiamenti della frequenza di pulsazione di queste stelle neutroniche sono stati collegati a terremoti nella crosta solida. La possibilità di prevedere questi terremoti dipende dalla conoscenza dei valori della capacità e della conduttività termiche del liquido di Fermi che si trova sotto la crosta.

c) Orientazione nucleare.

La polarizzazione del momento angolare di spin dei nuclei atomici a basse temperature, oltre che nel raffreddamento nucleare, ha trovato altre interessanti applicazioni in fisica nucleare. Queste divennero possibili fra il 1940 e il 1950 con il rapido sviluppo della spettroscopia dei livelli energetici nucleari conseguito mediante l'impiego di apparecchi più perfezionati per il conteggio delle radiazioni. L'analisi teorica della radiazione gamma emessa dai nuclei radioattivi ha mostrato che, oltre alla ben nota radiazione elettrica di dipolo - impiegata nel classico esperimento di Hertz sulla produzione di onde elettromagnetiche - devono essere prese in considerazione anche le radiazioni di quadrupolo, di ottupolo e anche di multipoli di ordine più elevato. Mentre la radiazione di dipolo ha momento angolare J = 1, misurato in unità ℏ, per quella di quadrupolo si ha J = 2. Per la legge di conservazione del momento angolare, un decadimento degli stati eccitati del ⁶⁰Ni, per esempio (v. fig. 45), può avvenire soltanto mediante la radiazione di quadrupolo. Quest'ultima è legata all'isotropia dello spazio e alle leggi della meccanica quantistica che assegnano un ben determinato momento angolare I agli stati energetici discreti del nucleo. Entro questi limiti le proprietà ditali stati sono dettate dalle interazioni forti tra nucleoni. Consideriamo ora il primo stato eccitato del ⁶⁰Ni con momento angolare I = 2h. Se i momenti angolari di tutti i nuclei sono allineati lungo un asse fisso nello spazio, per esempio quello di un campo magnetico esterno, la situazione così creata è chiaramente anisotropa. Tuttavia, nello stato finale del nucleo non vi è più momento angolare e tutta l'anisotropia deve risiedere nella radiazione emessa, cioè, la distribuzione dell'intensità dei raggi gamma emessi deve essere anisotropa rispetto al campo esterno. La verifica sperimentale si può attuare in vari modi indiretti, ma la prova più diretta del carattere di quadrupolo della radiazione nel caso del ⁶⁰Ni richiede l'allineamento degli spins nucleari a basse temperature. Questo risultato fu ottenuto a Oxford e a Leida nel 1951, e da allora è stato ottenuto anche in molti altri laboratori e per i nuclei di molti altri elementi (v. fig. 46). Poiché il grado di polarizzazione nucleare dipende da μ•H, i risultati di esperimenti di orientazione nucleare sono stati utilizzati anche per determinare i momenti magnetici dei nuclei di elementi radioattivi. Tali nuclei sono generalmente disponibili soltanto in quantità così esigua che altri metodi di misura, come ad esempio la risonanza magnetica, non sono praticabili.

Quanto è stato detto circa l'emissione di raggi gamma vale anche per l'emissione beta, come ad esempio la transizione dal ⁶⁰Co al secondo stato eccitato del nucleo del ⁶⁰Ni. Nel 1957 fu fatta a Washington la sorprendente scoperta che l'anisotropia nella distribuzione della radiazione beta, a differenza di quanto avviene per la radiazione gamma, non presenta simmetria speculare (v. fig. 47A).

Osserviamo che il vettore che rappresenta il momento angolare associato a una massa rotante presenta un verso che è invariante per riflessione speculare. Quindi, nel mondo riflesso in uno specchio, lo spin nucleare sarebbe ancora orientato verso l'alto come quello indicato nella fig. 47A, mentre la distribuzione di intensità sarebbe come quella della fignra 47B. Le particelle beta, a quanto risulta, sono emesse di preferenza in direzione antiparallela allo spin nucleare. Ora, l'emissione di antiparticelle si comporta invece in maniera opposta, come fu scoperto a Leida nel 1957.

Questi fenomeni vanno sotto il nome di ‛non conservazione della parità', dove il termine ‛parità' si nfensce al comportamento della funzione d'onda quantomeccanica rispetto a operazioni di riflessione speculare. Questa violazione della simmetria speculare è stata osservata anche in tutti quei processi di decadimento di particelle elementari che sono dovuti alle ‛interazioni deboli'.

Tali interazioni deboli spiegano il decadimento di un neutrone in un protone, in un elettrone e in un antineutrino in un tempo dell'ordine di minuti, mentre i processi di decadimento gamma dei nuclei si verificano in tempi dell'ordine di 10^-10-10^-15 secondi. La mancanza di simmetria in queste interazioni deboli non si manifesta solo nelle proprietà spaziali della radiazione emessa. Dalla fig. 47 risulta ovvio che la sostituzione della materia (fig. 47A) con l'antimateria (fig. 47B) non lascia invariata la distribuzione di intensità. La violazione di queste leggi di simmetria è forse un fatto di natura fondamentale, che permane tuttora inesplicabile.

La polarizzazione nucleare dei protoni alle temperature intorno ai millikelvin è stata raggiunta con una raffinata tecnica di microonde. Se si irradiano con microonde certi solidi che contengono impurità magnetiche, tenuti a basse temperature e sottoposti a campi statici, si ha una forte polarizzazione degli spins elettronici, che viene poi trasferita al sistema degli spins nucleari. In questo modo può ottenersi una polarizzazione degli spins dei protoni superiore al 9o%. Campioni di materiali contenenti protoni polarizzati vengono utilizzati per lavori di fisica delle alte energie: fasci di particelle elementari prodotti da un acceleratore, e in particolare fasci di pioni a vita breve, quando vengono diffusi da protoni polarizzati danno importanti indicazioni sulle caratteristiche dell'urto fra le particelle elementari in conformità con le leggi della meccanica quantistica e della relatività speciale.

Finora non ci siamo preoccupati di come si producano i campi magnetici di intensità sufficiente per raggiungere la polarizzazione nucleare. Nella maggior parte dei casi non è possibile utilizzare magneti da laboratorio, essendo quelli a nuclei di ferro limitati a circa 20-30kOe. Per l'orientazione nucleare si sono sfruttati i campi magnetici molto più intensi che esistono all'interno degli ioni magnetici: tali campi, che raggiungono valori fino a un milione di oersted, nascono da una leggera differenza nelle densità di spin degli elettroni appaiati del guscio interno degli ioni magnetici. Per esempio, rimuovendo uno dei due elettroni più interni di un elemento abbastanza pesante, come l'europio, si produce un campo di circa 10¹¹ Oe nel nucleo.

d) Termometria, equilibrio termico e fluttuazioni termiche.

La definizione termodinamica di temperatura è strettamente legata a quella di entropia; per esempio, il ragionamento che ha portato all'equazione (55) era basato sull'uguaglianza dell'entropia in due situazioni assai differenti, dalla quale si può ricavare una relazione assai semplice tra le temperature in queste due situazioni. In pratica, tuttavia, vi sono difficoltà notevoli nel tarare apparati termometrici secondo una vera temperatura termodinamica. Un sistema particolarmente adatto a determinare la temperatura dell'elio liquido tra 1 °K e 4 °K consiste nel misurare la pressione del suo vapore. Ci sono voluti molti anni perché gli specialisti di laboratori in varie parti del mondo potessero mettersi d'accordo almeno provvisoriamente sulla taratura da usare.

Le difficoltà aumentano al diminuire della temperatura, perché crescono rapidamente i tempi necessari allo stabilirsi di una temperatura uguale fra le varie parti dell'apparato sperimentale o, peggio ancora, tra varie parti fisicamente distinguibili di un unico pezzo di materia. Per esempio, per raffreddare a 0,01 °K un cristallo fissato a una superficie di metallo fredda possono occorrere delle ore, e il minimo passaggio di calore al cristallo può comportare una notevole differenza di temperatura tra quest'ultimo e il metallo. Ciò è dovuto alla scarsa conduttività termica del cristallo, e inoltre alla resistenza termica della superficie di separazione, detta anche ‛resistenza di Kapica'.

Kapica trovò che il passaggio di calore dall'elio liquido ai solidi diventa piccolo a bassa temperatura. Dato che il calore può essere estratto dall'⁴He solo sotto forma di onde acustiche o di fononi, e considerato che per bassi valori di T i fononi sono pochissimi, non può esservi un grande trasferimento di calore. Inoltre, la difformità delle proprietà elastiche dei due mezzi impedisce alle onde acustiche di passare dal solido all'elio e viceversa. Nel caso di contatti tra solidi si manifestano fenomeni analoghi a quelli appena considerati, che impediscono il raffreddamento di molte sostanze in tempi accettabili.

Il trasferimento di calore da una sostanza all'altra è generalmente trattato in un contesto diverso da quello dell'equilibrio termico in una stessa sostanza, essendo quest'ultimo di solito analizzato nel quadro dei fenomeni di rilassamento. Per esempio, la temperatura delle vibrazioni reticolari di un cristallo magnetico può essere ridotta alla regione dei millikelvin, mentre allo stesso tempo i momenti magnetici ionici nel medesimo cristallo possono mantenere una temperatura praticamente infinita per una durata di parecchi minuti. Per gli spins nucleari la situazione può essere ancora peggiore, dato che i tempi di equilibrio a tali basse temperature divengono spesso troppo lunghi per essere in pratica misurabili (superiori a un paio di settimane). L'allungamento del tempo di rilassamento termico alle basse temperature è dovuto, da una parte alla sparizione delle fluttazioni termiche, che è proporzionale a kT, e dall'altra all'esiguità delle energie normalmente coinvolte (come per i momenti magnetici nucleari interagenti nei cristalli).

Le misure di temperatura richiedono, oltre all'equilibrio termico, una relazione semplice e sicura tra la grandezza misurata e la temperatura stessa. La legge di Curie per la suscettività magnetica χ ∝ l/T degli ioni magnetici e dei momenti nucleari soddisfa questa condizione ed è stata perciò largamente usata in passato. Tuttavia si incontrano spesso varie complicazioni, dal momento che questa legge perde la sua validità al di sotto di una temperatura minima che qualche volta è addirittura di 1 °K.

Già da tempo la teoria e gli esperimenti sul rumore termico avevano dimostrato che in ogni resistenza elettrica esiste una tensione fluttuante ΔV, secondo il teorema di Nyquist:

-(-Δ-V-)² = 4kTR,

dove R rappresenta la resistenza e kT l'energia di fiuttuazione termica. È stato recentemente dimostrato che questa relazione rimane valida fino nella regione dei millikelvin, di modo che si può utilizzare il rumore delle resistenze per misurare in modo abbastanza semplice la temperatura (v. fig. 48).

Essendo stata così dimostrata l'assenza quasi totale di rumore alle basse temperature, sono stati inventati dei rivelatori di vari tipi per sfruttare i vantaggi di un migliore rapporto segnale-rumore. Strumenti bolometrici per la rivelazione della radiazione infrarossa lontana, per esempio dello spettro di corpo nero dello spazio interstellare, potrebbero acquistare la stessa importanza che hanno le tecniche maser usate oggi nelle osservazioni astronomiche nell'intervallo delle microonde. La riduzione del rumore alle basse temperature potrebbe anche essere sfruttata per rivelare le onde gravitazionali, che presumibilmente si originano dal collasso di una stella. Finora per rivelare queste onde ci si è serviti di un rilevatore di alluminio del peso di alcune tonnellate funzionante a temperatura ambiente. Poiché lo stato attuale della tecnologia consente di raffreddare un tale rivelatore fino a temperature dell'ordine dei millikelvin, si potrebbe migliorare di un fattore 10⁵ il rapporto segnale-rumore, il che permetterebbe agli astronomi di rivelare le esplosioni delle supernove, forse perfino all'esterno della nostra Galassia.

6. Applicazioni tecniche e sviluppi futuri.

Prima del 1940 la criofisica era studiata solo in un certo numero di laboratori altamente specializzati. Solo dopo la seconda guerra mondiale, quando divennero commercialmente disponibili liquefattori e contenitori per la conservazione dell'elio liquido, è nata la possibilità delle applicazioni tecniche della criofisica.

La maggior parte di queste applicazioni utilizza la superconduttività, ma ve ne sono anche di altro tipo.

Se il primo stadio di un amplificatore viene fatto funzionare alle temperature dell'elio liquido, il rumore termico può essere sensibilmente ridotto. Questo principio è stato applicato con successo ai collegamenti radio intercontinentali a mezzo di satelliti, usando soprattutto i masers.

Per ottenere un vuoto molto spinto si può sfruttare l'assorbimento dei gas su una superficie fredda. Questo principio è detto ‛pompaggio a freddo'. La ‛criopompa' non va utilizzata se non a pressioni inferiori a 10^-3 o 10^-4 torr per evitare che sulla superficie fredda si condensino strati di gas; ma se si prende questa precauzione, si possono raggiungere delle velocità di pompaggio estremamente alte (superiori a 10⁵ 1/s), e a pressioni dell'ordine di 10^-6 torr si possono raggiungere dei tempi di pompaggio superiori alle 1.000 ore prima che la superficie sia saturata. È utile rendere molto ruvida la superficie assorbente: per esempio, nel pompaggio a freddo dell'idrogeno, si riesce ad accrescere sensibilmente la capacità coprendo la superficie di pompaggio con anidride carbonica o ammoniaca solida.

A prima vista potrebbe sembrare conveniente far funzionare a basse temperature le linee di trasmissione di energia elettrica, perché la minore resistività (v. sopra, cap. 2, È b, 1) riduce le perdite di energia lungo i cavi. Tuttavia, il funzionamento di tali linee alle temperature dell'aria liquida o dell'azoto liquido non è economico perché la riduzione della resistenza è troppo piccola e comporta un'alta velocità di evaporazione del liquido di raffreddamento. D'altra parte, neanche il funzionamento alle temperature dell'elio è economico perché il calore d'evaporazione è troppo basso. Potrebbe forse dare migliori risultati l'uso di temperature vicine a quelle del neon e dell'idrogeno liquidi, purché i conduttori fossero di rame o di alluminio purissimi e privi di difetti. Ciononostante, la complicazione e la vulnerabilità del sistema di cavi sembrano rendere anche questo sistema praticamente inutilizzabile.

Una possibilità alternativa sarebbe evidentemente l'uso di linee superconduttrici raffreddate a elio. Nel caso di superconduttori di tipo II (gli unici utilizzabili in questo caso), le perdite di potenza sono uguali a zero per la corrente continua, ma non sono invece rigorosamente nulle per la corrente alternata, a causa degli effetti di isteresi magnetica trattati nel cap. 4, È b. Ovviamente le linee elettriche superconduttrici sono altrettanto vulnerabili e complicate quanto i normali cavi metallici criogenici, ed è stato calcolato che la riparazione di un cavo superconduttore sotterraneo potrebbe richiedere dei mesi. Per brevi distanze, questo tipo di cavo non sarà mai economicamente utilizzabile a causa delle inevitabili perdite di calore alle estremità. Per distanze assai maggiori di 10 km, invece, essi potrebbero diventare convenienti per potenze superiori a 2.000 megawatt. È stato osservato che in zone con altissime densità di popolazione, come Londra, New York e Tōkyō, la produzione di calore per effetto Joule nel tradizionale sistema di cavi sotterranei è talmente elevata che già oggi si nota una preoccupante essiccazione del suolo la quale dà luogo a un sensibile abbassamento degli edifici. Così, in futuro, l'uso di cavi criogenici potrà forse diventare necessario, anche se i molti e difficili problemi tecnici ancora da risolvere ne rendono improbabile la realizzazione prima del 1990.

Quando sarà possibile costruire cavi superconduttori, acquisteranno interesse anche grossi trasformatori, generatori e motori superconduttori. Questi hanno il vantaggio, rispetto ai cavi, che le loro dimensioni relative li rendono più adatti a essere montati in contenitori criogenici. I motori e i generatori a corrente continua, specialmente quelli omopolari sono senz'altro possibili, ma anche quelli a corrente alternata sono in teoria attuabili. In questo secondo caso, al crescere delle dimensioni del motore le perdite elettriche diminuiscono più velocemente di quanto cresca la potenza di raffreddamento necessaria per raffreddare i conduttori. Le bobine superconduttrici sono più vantaggiose delle armature superconduttrici: esse permettono una densità di flusso magnetico molto più alta di quelle normali e quindi una macchina di dimensioni date avrebbe una potenza maggiore, oppure, si potrebbe usare una macchina più piccola per una potenza data. Quest'ultimo caso è di particolare interesse per aeroplani e sottomarini, ma, in generale, le macchine superconduttrici diventano più economiche di quelle normali solo per potenze di centinaia di megawatt.

La superconduttività ha già da vari anni trovato pratica utilizzazione nella produzione di campi magnetici intensi. Magneti con il nucleo di ferro possono produrre campi fino a circa 30 kOe. Con bobine di rame a temperatura ambiente si possono raggiungere campi compresi tra i 100 e i 200 kOe, ma soltanto con un consumo di potenza di vari megawatt. Ciò, inoltre, comporta un enorme impianto di raffreddamento. Costruendo invece le bobine di materiale superconduttore con campi di perturbazione sufficientemente alti (v. sopra, cap. 4), si possono ottenere campi simili con consumi di potenza quasi trascurabili.

Nel 1961 si trovò che il composto intermetallico Nb₃Sn ha un campo di perturbazione di circa 190 kOe. Purtroppo, però, questo materiale è troppo fragile per poter essere impiegato senza difficoltà per fili e bobine. Le leghe 3NbZr e NbTi hanno campi di transizione inferiori, ma sono assai più duttili. Attualmente le bobine per campi fino a 80 kOe sono di solito fatte di NbTi e quelle per campi più alti di Nb₃Sn o, negli ultimi tempi, di V₃Ga.

Queste bobine possono essere adoperate nel ‛modo persistente' producendo un corto circuito superconduttore dopo che il magnete è stato energizzato. In questo caso il campo rimane assai stabile nel tempo. In molti casi, però, è più conveniente usare un rettificatore a bassa potenza e ad alta corrente. L'introduzione di varie centinaia di ampère in un criostato di elio liquido non costituisce più un serio problema.

Durante l'eccitazione di una bobina il flusso magnetico penetra nel materiale superconduttore stesso dando origine a quegli effetti di fissaggio e di salto di flusso che abbiamo discusso nel cap. 4, È g. Si ha così un riscaldamento del filo che, a sua volta, fa diminuire la corrente critica. Quindi la corrente massima di una bobina superconduttrice è minore di quella che si avrebbe nel filo prima di avvolgerlo; si tratta di un effetto che fu osservato nei primi esperimenti con magneti superconduttori e che viene di solito detto ‛degradazione della corrente' o ‛effetto di prossimità degli avvolgimenti'. Questo effetto è tanto più pronunciato quanto più rapidamente viene energizzata la bobina.

In effetti, l'improvvisa interruzione della corrente è pericolosa per due motivi. L'energia magnetica totale ½LI², dove L è l'autoinduzione della bobina e I la corrente, viene convertita in energia termica, il che alla fine si risolve nella rapida evaporazione di una notevole quantità di elio liquido e nell'aumento di pressione che l'accompagna. Inoltre, tra gli avvolgimenti nasce una forza elettromotrice indotta LdI/dt piuttosto alta, che può danneggiare la bobina.

Di solito per proteggere il conduttore di NbTi lo si ricopre di rame e questo, a sua volta, di uno strato isolante. Il rame permette alla corrente un cammino alternativo nel caso di perturbazioni locali, di modo che la regione normale ha la possibilità di ristabilirsi. Oltre a ciò, le correnti parassite nel rame rallentano la velocità di penetrazione del flusso nel superconduttore, e la massa termica addizionale riduce gli effetti di riscaldamento. Evidentemente, più rame si aggiunge al NbTi, migliore diventa la stabilizzazione e più la corrente massima della bobina si avvicina alla corrente critica del materiale stesso. D'altra parte, però, una grande quantità di rame produce una bassa densità di corrente media sull'insieme del conduttore e si ha quindi un magnete ingombrante che richiede un grosso vaso dewar e una gran quantità di elio liquido per il raffreddamento iniziale.

Per questo motivo il nocciolo di NbTi viene spesso suddiviso in un gran numero di sottilissimi filamenti attorcigliati immersi in una matrice di rame. Più sottili sono i filamenti e più bassa è la produzione di calore, e al di sotto di circa 10 micron si trova che l'NbTi diviene ‛intrinsecamente stabile', di modo che è necessaria soltanto una quantità di rame relativamente piccola e la degradazione di corrente è trascurabile. A causa della drastica riduzione delle correnti persistenti nel materiale superconduttore, la relazione tra il campo della bobina e la corrente che la attraversa è più facilmente reversibile per i magneti a molti filamenti che per quelli a nucleo omogeneo. Ciò presenta anche il vantaggio che il campo rimanente, dopo la riduzione a zero della corrente, è sensibilmente più piccolo. Tuttavia, anche nelle bobine a molti filamenti si incontra una nuova fonte di instabilità, dovuta a piccoli movimenti dei conduttori nel campo che danno origine a correnti di induzione. Si può ovviare a questo effetto fissando bene gli avvolgimenti, il che di solito si fa impregnando l'intera bobina dopo averla avvolta. La fig. 49 mostra lo spaccato di un cavo commerciale consistente di 1045 filamenti di NbTi di 0,01 mm di spessore immersi nel rame. Il diametro totale del conduttore è di 0,5 mm.

Il problema della fragilità del Nb₃Sn (o del V₃Ga) viene risolto combinando un sottilissimo strato di Nb₃Sn con un conduttore ad alta resistenza meccanica. La fig. 50A ne dà un esempio. Il conduttore riportato nella figura viene costruito ricoprendo una striscia di niobio, da entrambi i lati, con sottili strati di stagno e trattandola poi a caldo a 930 °C. Questo porta alla formazione di strati di Nb₃Sn dello spessore di 2,2 micron (v. fig. 50B) che nello stato superconduttore possono sopportare una densità di corrente di 2,6 × 10⁵ A/cm² a 100 kOe. Per stabilizzarla, la striscia viene saldata tra due fogli di rame ricoperti a loro volta di acciaio inossidabile che serve per renderla forte. Lo spessore del nastro è di solito di alcuni centesimi di millimetro. Esso non deve essere piegato troppo per evitare danni allo strato di Nb₃Sn e questo pone un limite inferiore al diametro interno della bobina del magnete.

La fig. 51 mostra le tre sezioni di un magnete a bobina superconduttrice costruito nel laboratorio Kamerlingh Onnes dell'Università di Leida. Le due sezioni interne sono di nastro di Nb₃Sn e quella esterna di filo di NbTi. Il diametro interno dell'intero magnete è di 28 mm, quello esterno di 160 mm. Le tre sezioni vengono energizzate in serie, e a 4,2 °K si raggiunge un campo di 91 kOe•A 1,5 °K il campo massimo è 114 kOe. Ora vi sono in commercio dei magneti di dimensioni paragonabili e con campi fino a 150 kOe che sono usati per ricerche scientifiche in vari laboratori.

È possibile ottenere dei campi magnetici ancora più intensi montando una bobina di rame funzionante a temperatura ambiente in una superconduttrice immersa in elio liquido. Con tali magneti ‛ibridi' si possono produrre campi molto al di sopra dei 200 kOe.

Oltre a questi magneti da laboratorio per campi molto intensi, sono stati costruiti o sono in costruzione degli impianti per la produzione di campi moderati su volumi molto grandi, per esempio camere a bolle o reattori a fusione. Nella fig. 52 è riportato un disegno della camera a bolle a idrogeno liquido dell'Argonne National Laboratory. Il diametro della camera a bolle stessa è di 366 cm e l'altezza è di circa 300 cm. Le bobine hanno un diametro interno di 475 cm e la loro lunghezza totale è 280 cm. Esse sono racchiuse in grossi contenitori di elio a forma di anello circondato da un grosso giogo di ferro. Il campo a cui funzionano è di 18 kOe a 2.000 A, e l'energia totale ‛ L1₂ è 80 megajoules. Un magnete per camera a bolle ancora più grande è in costruzione al Centre Européen de Recherche Nucléaire di Ginevra: ha un diametro di 472 cm, un'altezza di 400 cm e avrà un campo di 35 kOe e un'energia di 800 megajoules. La fig. 53 mostra metà del sistema di avvolgimenti.

Un'applicazione speciale dei magneti superconduttori che potrebbe divenire importante in futuro è la levitazione di treni a lunga percorrenza. Un treno che ‛galleggia' 25 cm al di sopra della sua sede può raggiungere delle velocità molto più alte del treno tradizionale su rotaie. Una soluzione possibile è quella delineata nella figura 54A.

Un magnete che si muove sopra una piastra conduttrice viene respinto dalle correnti parassite che il suo moto produce nel metallo. La figura mostra un veicolo pressappoco cilindrico in una guida a forma di ‛grondaia' che circonda il terzo inferiore della sua circonferenza. Nella parte inferiore del veicolo, al di sotto del compartimento dei passeggeri, sono sistemati degli intensi magneti superconduttori che producono campi alternati verso l'alto e verso il basso. Tra questi magneti sono situate varie coppie di ruote retrattili usate solo in fase di accelerazione e di decelerazione, per velocità inferiori a 60 km all'ora.

La guida a forma di grondaia consiste di tre sezioni parallele. Le due esterne sono fogli di alluminio che forniscono la levitazione, mentre quella centrale è praticamente un motore lineare sincrono, costituito da un certo numero di strisce di alluminio piegate a forma di serpentina, come nella fig. 54B, ognuna delle quali ha lo stesso periodo del campo magnetico del treno. Un campo magnetico mobile viene ottenuto energizzando ciascuna striscia con la fase opportuna con corrente alternata prodotta da impianti lungo la linea. Ogni tratto di 5 km riceve energia da stazioni diverse le cui frequenze, ampiezze e fasi possono essere regolate indipendentemente sulla base di informazioni trasmesse dal treno stesso. Più alta è la frequenza e maggiore la velocità. La regolazione della fase e dell'ampiezza è importante soprattutto per l'accelerazione e la decelerazione. Si pensa che all'aria aperta si possano raggiungere velocità di 500 km all'ora, ma in una galleria in condizioni di vuoto parziale questo veicolo potrebbe competere con gli aerei a reazione. Progetti di treni a superconduttori sono allo studio in America, in Giappone e in Germania.

La repentina transizione dei superconduttori di tipo I dallo stato normale a quello superconduttore e viceversa può essere usata per gli elementi di memoria dei calcolatori. Una delle possibilità è il ‛criotrone', che consiste di un sottile filo di tantalio circondato da una piccola bobina di niobio. A 4,2 °K sia il Ta che il Nb sono superconduttori, ma il campo di perturbazione del Ta è molto più basso. Così, facendo passare una piccola corrente attraverso la bobina di Nb, il filo di Ta diviene normale. Se i fili di Ta di due criotroni sono collegati in parallelo in un circuito, un breve impulso di corrente attraverso una bobina di niobio fa passare l'intera corrente del circuito all'altro filo di tantalio e, per l'autoinduzione dei fili, essa continua a fluire anche dopo che è passato l'impulso. Si ha così un semplice effetto ‛flip-fiop' di piccole dimensioni. Negli ultimi tempi, però, a causa del rapido sviluppo dei microtransistori, gli elementi di memoria superconduttori hanno perso una parte del loro interesse.

Alcune recenti applicazioni della superconduttività sono basate sulla giunzione di Josephson. Dato che l'ampiezza della corrente di tunnel può essere misurata con grande precisione, risulta ovvio dalla fig. 38 (v. sopra, cap. 4, È 1) che è possibile una determinazione molto accurata delle intensità del campo magnetico. Se la giunzione consiste di una punta acuminata premuta contro un foglio di metallo, la differenza tra due zeri consecutivi della fig. 38A può essere dell'ordine di 1 Oe. Una precisione molto più alta si ottiene collegando due giunzioni in parallelo, sfruttando la figura di interferenza molto fine della figura 38B. Questo sistema, che è stato chiamato uno SQUID (che sta per Superconducting QUantum Interference Device), permette di rivelare variazioni dell'ordine di 10^-7 Oe in un campo di 2.500 Oe.

Collegando in parallelo a un filo due giunzioni Josephson, una corrente che passa attraverso il filo dà origine a un campo magnetico nell'area compresa tra le giunzioni. Questo ha portato alla costruzione di un semplicissimo galvanometro (detto SLUG, ossia Superconducting Lowinductance Undulating Galvanometer) con una sensibilità dell'ordine di 1 microampère e con resistenza trascurabile. Collegando una resistenza di 10^-8 ohm a uno SLUG si ottiene un voltmetro con la straordinaria sensibilità di 10^-14 volt.

Anche se non abbiamo fatto un elenco completo delle applicazioni pratiche della criofisica, risulta chiaro da quanto detto sopra che le basse temperature avranno un ruolo sempre più importante in futuro e che tra qualche decennio l'elio liquido potrebbe divenire una sostanza di uso quotidiano e ovunque disponibile.

Bibliografia.

Atkins, K. R., Liquid helium, Cambridge 1959.

Flügge, S. (a cura di), Encyclopedia of physics, voll. XIV-XV, Low temperature physics, Berlin 1956.

Gorter, C. J. (a cura di), Progress in low temperature physics, voll. I-VI, Amsterdam-London 1955-1970.

Hudson, R. P., Principles and application of magnetic cooling, Amsterdam 1972.

Keesom, W. H., Helium, Amsterdam-London-New York 1942.

Kittel, C., Introduction to solid state physics, New York 1966³.

Klerk, D. de, Construction of high field electromagnets, Newport Pagnell, 1965.

London, F., Superfluids, 2 voll., New York 1950-1954.

Long, H. M., Gauster, W. F. (a cura di), Proceedings of the applied superconductivity conference, Annapolis 1972.

Lynton, E. A., Superconductivity, London 1962.

Mendelssohn, K., The quest for absolute zero, London 1966.

Montgomery, D. B., Solenoid magnet design, London 1969.

Parkinson, D. H., Mulhall, B. E., The generation of high magnetic fields, London 1967.

Parks, R. D. (a cura di), Superconductivity, 2 voll., New York 1969.

Rose-Innes, A. C., Rhoderick, E. H., Introduction to superconductivity, London 1969.

Saint-James, D., Sarma, G., Thomas, E. J., Type II superconductors, London 1969.

Wilks, J., Introduction to liquid helium, Oxford 1970.