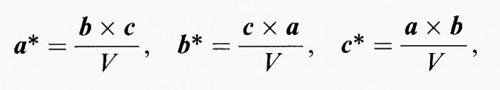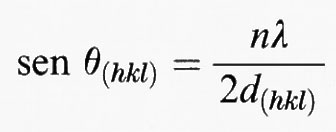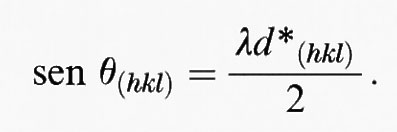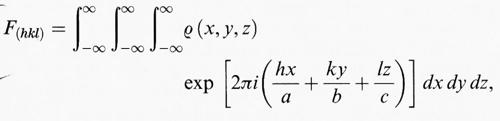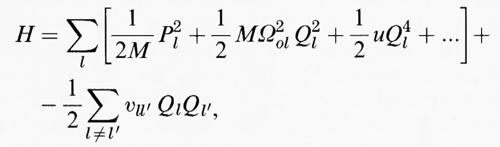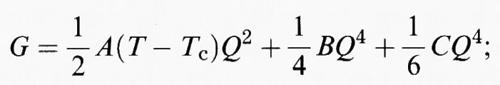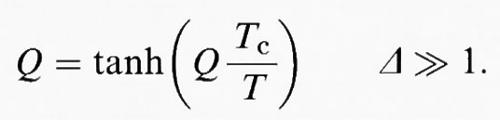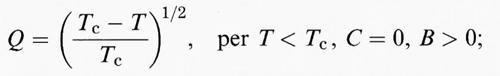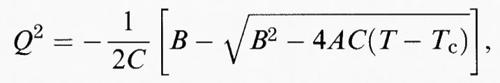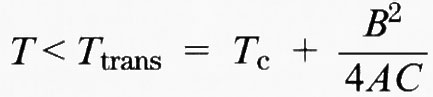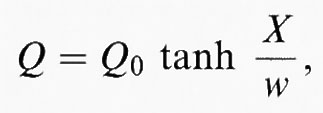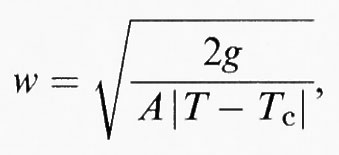Cristallografia

Cristallografia

SOMMARIO: 1. Introduzione.  2. Concetti di simmetria: a) gruppi e reticoli; b) rappresentazioni irriducibili dei gruppi spaziali.  3. Diffrazione di radiazioni da parte dei cristalli.  4. Transizioni di fase strutturali.  5. Conclusioni e prospettive. □ Bibliografia.

1. Introduzione

Nel XVIII secolo - dopo un lungo periodo ‛prescientifico', durante il quale i cristalli furono l'oggetto di credenze mitologiche, studi sporadici ed estese attività commerciali - la natura dello stato cristallino cominciò a essere sottoposta alle prime indagini sistematiche. L'osservazione sperimentale, all'epoca, era sostanzialmente limitata agli aspetti più ovvi della morfologia dei cristalli, vale a dire agli angoli caratteristici formati tra facce adiacenti, e lo strumento utilizzato in questi studi era il goniometro meccanico. La maggior parte dei minerali costitutivi delle rocce, dei noduli mineralizzati e di altri campioni naturali era generalmente esclusa da tali studi, perché le facce ben sviluppate che essi mostravano erano poche o nessuna. Pertanto la cristallografia fu inizialmente una scienza ben distinta dalla mineralogia e dalla chimica. Gli studi morfologici e, qualche tempo dopo, l'ottica cristallografica furono le attività principali delle prime indagini sperimentali in cristallografia, che pertanto si legò piuttosto saldamente alle scienze fisiche.

L'ipotesi della distribuzione periodica di quelli che noi ora chiamiamo atomi o molecole era anch'essa largamente accettata all'epoca, sebbene sia stata verificata sperimentalmente solo all'inizio di questo secolo con l'avvento dei metodi diffrattometrici di Laue (v., 1912) e Bragg (v., 1913). La scoperta che i cristalli presentano vaste zone (su scala atomica) caratterizzate da una configurazione periodica avvalorò anche i concetti di simmetria, alcuni dei quali erano stati enunciati molto tempo prima (v., ad es., Bravais, 1866). Essi erano fondati sulle strutture geometriche di base che, come in un mosaico, riempiono completamente uno spazio a due o tre dimensioni obbedendo a regole definite, come quelle imposte dalla composizione chimica e dalla riproduzione della morfologia ideale del cristallo.

L'uso sistematico dei metodi diffrattometrici che impiegano varie sorgenti di radiazione (raggi X, neutroni, elettroni, radiazioni γ) determinò lo sviluppo dei diversi apparati strumentali che sono ora ampiamente usati per l'analisi delle strutture atomiche dei cristalli. L'analisi delle strutture cristalline dei minerali più abbondanti e dei materiali importanti per le loro proprietà fisiche divenne presto un'indagine di routine, che determinò, tra il 1960 e il 1980, un profondo mutamento della cristallografia. Molti istituti di ricerca che si erano dedicati all'ordinaria analisi delle strutture cessarono di esistere, mentre altri svilupparono la loro attività cristallografica in un modo nuovo. Un gran numero di cristallografi cominciò a lavorare su materiali organici, principalmente biologici, e raggiunse un grande successo nel campo della biocristallografia, dell'ingegneria farmaceutica e in campi affini. Molti cristallografi lavorano in laboratori chimici nei quali le tecniche dell'analisi strutturale sono considerate come uno dei più efficaci mezzi analitici. I cristallografi ‛fisici' estesero i loro studi alle strutture aperiodiche, alle superfici, ai difetti strutturali, alla dinamica reticolare, alle transizioni di fase strutturali, ecc. In questi campi, molte delle osservazioni sperimentali principali sono fatte a una scala molto maggiore della distanza di ripetizione tra gli atomi, e pertanto per descrivere le caratteristiche strutturali di una configurazione atomica a una scala compresa tra la sua struttura atomica e le sue dimensioni macroscopiche si fa uso del termine generico di ‛cristallografia mesoscopica'.

Se vogliamo definire la cristallografia in base a ciò su cui lavorano i cristallografi, possiamo per prima cosa considerare che l'aspetto comune a tutti i loro studi è la determinazione della disposizione degli atomi in determinati corpi. Questi corpi spesso sono cristalli, ma possono anche essere i ‛cristalli liquidi' o i vetri con o senza ordine a corto raggio, le superfici, le schiume, le proteine, ecc. L'approccio sperimentale più comune è probabilmente ancora basato sulle tecniche di diffrazione, sebbene integrate da altre misurazioni, come quelle tendenti a determinare le proprietà magnetiche e dielettriche. È difficile dare una definizione precisa e completa della cristallografia: molti scienziati in campo cristallografico possono infatti definirsi tanto cristallografi quanto anche fisici, chimici, mineralogisti, scienziati della materia, biochimici, ecc.

2. Concetti di simmetria

a) Gruppi e reticoli.

I cristallografi fanno sistematicamente uso del concetto che le strutture cristalline possono essere descritte per mezzo di specifiche operazioni di simmetria. Vediamo di chiarire con un esempio le più elementari di tali operazioni. Se ruotiamo la disposizione atomica della fig. 1 di 90° intorno al centro del disegno, ritroviamo la stessa figura, e lo stesso accade anche in seguito a rotazioni di 180°, 270° e 360°. Le ‛rotazioni' sono generalmente descritte attraverso il numero n mediante il quale esse dividono i 360° dell'angolo giro. Nel nostro esempio, 90° = 360°/4, e quindi n = 4; pertanto, l'asse di simmetria viene chiamato ‛asse quaternario'. Esistono altri tipi di assi di rotazione, come quelli senario (per n = 6), ternario (n = 3) e binario (n = 2). Nel caso di un motivo che si ripete per traslazione (v. fig. 2) non possono esistere assi di ordine 5 o 7. La spiegazione geometrica è la seguente. Ammettiamo l'esistenza di un asse con angolo di rotazione α in ciascun punto del reticolo; tale rotazione deve lasciare inalterato non solo ciascun punto ma anche l'intera conformazione (motivo), che possiamo immaginare estesa all'infinito in tutte le direzioni dello spazio. La grandezza della traslazione, indicata con b in fig. 2, non può essere variata per effetto della rotazione. Poniamo cha a sia un modulo di ripetizione tale che

b = ma = a + 2a cos α,

dove m è un numero intero; ne segue cos α = (m - 1)/2, per cui, al variare di m si ha che gli unici valori possibili per α sono 360°/n con n, = 1, 2, 3, 4 o 6. Si noti che tale argomentazione esclude altri valori di n solo a condizione che la configurazione sia caratterizzata da una ripetizione completa per traslazione e sia infinitamente grande (reticolo). Di fatto, esistono configurazioni con simmetria 5 nel caso di periodicità non traslazionali e di sistemi molecolari di dimensione finita.

Oltre alla simmetria per rotazione, sono basilari anche altri due tipi di simmetria: 1) la simmetria per ‛riflessione' rispetto a un piano, detto piano di simmetria, simile alla duplicazione di un oggetto visto in uno specchio (v. fig. 3); 2) l'‛inversione', che si ottiene tracciando linee le quali, passando attraverso un punto (detto ‛centro di inversione'), congiungono ogni punto con il suo equivalente per simmetria situato a distanza uguale e dalla parte opposta rispetto al centro suddetto.

Partendo da alcuni di questi elementi di simmetria si possono formare combinazioni che generano altri elementi di simmetria. Come esempio consideriamo un piano di simmetria e un asse binario a esso perpendicolare. Tutte le operazioni di simmetria in questo sistema sono compatibili con un'ulteriore operazione di simmetria, cioè con un'inversione rispetto a un punto posto all'intersezione tra il piano di simmetria e l'asse binario. Tutte le combinazioni delle operazioni di simmetria devono essere anch'esse operazioni di simmetria, e per tutte le operazioni deve esistere un'operazione inversa che riconduca alla configurazione iniziale. Queste proprietà, unite al fatto che esiste sempre un'operazione di ‛identità' (rotazione di 0°) e che le operazioni sono associative [(a ⊗ b) ⊗ c = a ⊗ (b ⊗ c)], implicano che l'insieme delle operazioni di simmetria che lasciano una configurazione invariata è un gruppo nel senso matematico del termine (v. Bradley e Cracknell, 1971; v. Šubnikov e Koptsik, 1972). Questi gruppi sono chiamati ‛gruppi puntuali cristallografici': esistono 32 di tali gruppi puntuali.

Torniamo ora a quantificare ciò che intendiamo per simmetria. Consideriamo un oggetto che prima duplichiamo e poi trasliamo. Ripetiamo l'operazione con il nuovo oggetto e così via all'infinito. Ripetendo tutte queste operazioni con una traslazione in direzione opposta a partire dall'oggetto iniziale, arriveremo a una catena infinitamente lunga di oggetti equidistanti. La stessa operazione può essere effettuata sulla catena per produrre una disposizione periodica piana. Aggiungendo un'ulteriore traslazione in una direzione non complanare arriviamo a una configurazione tridimensionale e così via. Una configurazione periodica n-dimensionale, quindi, possiede n operazioni di traslazione indipendenti.

Per una descrizione matematica è irrilevante quale sia la natura fisica del nostro oggetto, che possiamo pertanto rappresentare come un punto. Le configurazioni n-dimensionali invarianti per traslazione sono chiamate ‛reticoli n-dimensionali'. Questi ci permettono di descrivere (o meglio, di approssimare) le strutture cristalline reali: i reticoli 1D (unidimensionali) sono adatti per le strutture a catena; i reticoli 2D (bidimensionali) per le strutture a strati, le superfici e le interfacce; i reticoli 3D (tridimensionali) per la maggior parte delle strutture cristalline. Reticoli a più di tre dimensioni sono usati per descrivere strutture atomiche che non sono periodiche in tre dimensioni: per esempio, reticoli a quattro dimensioni per le strutture incommensurate e reticoli a sei dimensioni per i quasi-cristalli.

Le simmetrie traslazionali possono essere combinate con le simmetrie per rotazione e riflessione. Si ottengono così nuovi tipi di operazioni di simmetria. La combinazione di un asse binario e di una traslazione lungo l'asse può servire da esempio. Un oggetto viene prima ruotato e poi traslato. Il nuovo oggetto così prodotto non è equivalente per traslazione e neppure per rotazione semplice al primo oggetto. Se applichiamo la stessa operazione al nuovo oggetto generiamo un terzo oggetto che è ora equivalente per traslazione al primo, con una grandezza di traslazione doppia rispetto a quella utilizzata prima. Il nuovo elemento di simmetria è chiamato ‛asse elicogiro binario'. Esistono assi elicogiri simili per tutte le rotazioni di ordine n. Per un piano di simmetria, l'operazione equivalente è lo ‛slittopiano'. Dal momento che la disposizione complessiva degli oggetti resterà invariata rispetto a tutte le operazioni di simmetria descritte, queste operazioni di simmetria devono di nuovo costituire dei gruppi: i cosiddetti ‛gruppi spaziali' (cristallografici). Vi sono 230 gruppi spaziali. Le traslazioni pure formano un sottogruppo che comprende tutti i possibili spostamenti paralleli che lasciano il reticolo invariato. I sette tipi possibili di reticoli semplici (che dipendono dall'uguaglianza o meno della grandezza di traslazione e dagli angoli uguali a 90°, 60°, 120° o altro) sono chiamati ‛reticoli di Bravais'.

Le argomentazioni svolte possono essere ampliate abbandonando la semplificazione matematica di considerare i nostri oggetti come punti, cioè come elementi privi di dimensione. Il passo successivo più semplice è considerare tali oggetti come entità unidimensionali di lunghezza unitaria. L'unico grado di libertà diventa allora l'orientazione, cioè possiamo immaginare i nostri oggetti come spins, o come valori di una qualsiasi altra variabile binaria (per esempio, + o -, nero o bianco). Nel mondo fisico, i nostri oggetti potrebbero essere degli atomi magnetici con uno spin in su o in giù. Possiamo ora riconsiderare tutte le possibili operazioni di simmetria includendo quelle relative alle simmetrie interne dei nostri oggetti. Esse costituiranno i cosiddetti ‛gruppi neri e bianchi' o ‛gruppi di Šubnikov'. Il numero complessivo di questi gruppi è 1.651. Aumentando il numero dei gradi locali di libertà da bianco/nero a motivi di base più complessi, si arriva ai ‛gruppi spaziali colorati'. Un gruppo spaziale a quattro colori potrebbe descrivere atomi quadrupolari, ecc. Abbiamo visto che il numero totale di gruppi spaziali per il semplice caso binario nero/bianco è già grande; non sorprende quindi che non sia stato ancora fatto alcun tentativo di analizzare l'intero insieme dei gruppi spaziali colorati con più di due colori.

b) Rappresentazioni irriducibili dei gruppi spaziali.

Le proprietà di simmetria permettono di definire un reticolo come un'impalcatura matematica che ‛sostiene' una struttura atomica. Pertanto la descrizione di una struttura cristallina deve precisare: a) che tipo di reticolo (o di reticoli) viene usato per riempire lo spazio; b) quali atomi, molecole, ecc. sono localizzati nei vari siti strutturali. È sempre utile considerare tale descrizione della struttura cristallina in termini geometrici come punto di partenza per analisi successive. Se ci domandiamo, per esempio, quali siano le distribuzioni delle funzioni d'onda elettroniche, delle vibrazioni reticolari, o di altre quantità fisiche, ci aspettiamo che tali distribuzioni riflettano le proprietà geometriche della struttura cristallina forniteci dal gruppo spaziale. Tale descrizione non è comunque completa. Come esempio consideriamo la distribuzione degli orbitali d intorno a un atomo posto al centro di un sito strutturale a forma di ottaedro. Gli elettroni si distribuiranno nel modo più idoneo a questo ambiente, anche se ci sono tre possibilità di farlo (v. fig. 8). Identificare le funzioni d'onda imposte dalla simmetria è un tipico compito dei cristallografi.

La parte della teoria dei gruppi cristallografici che tratta le relazioni che esistono tra gruppi spaziali e parametri fisici si chiama ‛teoria delle rappresentazioni dei gruppi' (v. Ljubarskij, 1957). Essa formalizza le operazioni di simmetria in un gruppo spaziale attraverso un operatore che spesso è una matrice che descrive la trasformazione del reticolo. Poniamo che g sia un elemento del gruppo G; in questo caso un operatore T (g) deve avere tutte le operazioni di simmetria di g, per esempio:

T (g₁g₂) = T (g₁) T (g₂).

In altre parole, possiamo trattare gli operatori in modo numerico invece che attraverso le più astratte operazioni di gruppo. La domanda è ora come un operatore T (g) possa trasformare un oggetto fisico, per esempio la funzione d'onda riportata nella fig. 8. Tale trasformazione viene definita facendo riferimento alle coordinate spaziali del reticolo, cioè l'operatore trasforma un vettore r in t •p r attraverso una matrice t. Se l'oggetto è ora una funzione d'onda ψ(r), definiamo l'azione dell'operatore T (g) come

T (g) • ψ (r) = ψ (t^-1 • r).

Questo approccio offre il vantaggio che l'oggetto dell'operatore T (g) è ora una quantità fisica (in questo caso la funzione d'onda) e non il reticolo cristallino. Si possono allora trattare tutte le equazioni fisiche con questo operatore e verificare se una data quantità cambia attraverso l'azione dell'operatore. Se non cambia, viene definita ‛invariante' ed è compatibile con la simmetria. Le quantità invarianti non richiedono una ridistribuzione degli atomi in una struttura cristallina e rappresentano stati con energia più bassa rispetto alle quantità non invarianti. Questo significa, per esempio, che gli stati elettronici fondamentali corrispondono a funzioni d'onda invarianti.

I cristallografi hanno sviluppato un approccio sistematico per l'uso degli operatori di una rappresentazione. Un problema importante è stabilire quanti parametri fisici dello stesso tipo possano appartenere alla stessa rappresentazione. Tale problema fa parte del problema più generale di definire quanti vettori fondamentali possano far parte di una rappresentazione. È possibile dividere una rappresentazione in unità più piccole che non possano essere ridotte ulteriormente? Se una rappresentazione opera in uno spazio unidimensionale, vi può essere solo un parametro fisico di un certo tipo che sia invariante. Se lo spazio è bidimensionale, allora vi sono due parametri invarianti ed essi non possono, in linea di principio, essere distinti tra loro tramite un esperimento fisico che sia compatibile con la simmetria cristallina. Anche per dimensioni di ordine maggiore vale lo stesso principio. Le rappresentazioni così definite vengono chiamate ‛irriducibili'; esse sono gli equivalenti, per l'analisi dei parametri fisici, dei gruppi spaziali che servono per la descrizione della distribuzione geometrica degli atomi in una struttura cristallina.

Lo sviluppo di metodi algebrici per l'uso della teoria delle rappresentazioni ha contribuito molto alla comprensione delle correlazioni tra le proprietà fisiche dei cristalli e la loro struttura atomica.

3. Diffrazione di radiazioni da parte dei cristalli

La tecnica sperimentale più efficace per l'analisi delle strutture atomiche è probabilmente la diffrazione di radiazioni con lunghezze d'onda di valore prossimo alle distanze interatomiche. Max von Laue (v., 1912), inaugurò questa tecnica usando la diffrazione di raggi X. Il principio basilare della diffrazione di raggi X, neutroni, elettroni, raggi γ è essenzialmente lo stesso: la radiazione del fascio incidente viene diffusa dagli atomi. Le onde diffuse (con ampiezze che sono caratteristiche di ciascun tipo di atomo) producono figure di interferenza che possono essere misurate macroscopicamente (v. Buerger, 1942; v. Cowley, 1984).

Un modo semplice per interpretare la figura di diffrazione fu proposto da sir W. Lawrence Bragg (v., 1913) poco dopo la scoperta degli spettri di diffrazione da parte di Laue. Egli prese in considerazione piani di atomi: le onde diffuse da piani successivi si rafforzano reciprocamente a certi angoli, se la differenza di cammino tra i raggi è un multiplo della lunghezza d'onda. Solo per questi angoli θ ci si aspetta che si verifichi una diffrazione misurabile macroscopicamente. Con semplici considerazioni geometriche si può dimostrare che l'interferenza costruttiva avviene se

2 d sen θ = nλ,

dove d è la distanza tra i piani atomici riflettenti, λ la lunghezza d'onda e n dà l'ordine dell'interferenza (v. Buerger, 1942).

Per caratterizzare una struttura cristallina, il problema geometrico fondamentale è determinare tutti i possibili valori delle distanze interatomiche d e l'orientamento dei piani corrispondenti. Questo problema fu di fatto risolto da Whewell e Miller nell'Ottocento, e fu poi definito meglio tramite la costruzione del ‛reticolo reciproco'. Partendo dal reticolo (diretto) descritto in precedenza, il reticolo reciproco può essere costruito nel modo seguente: si tracci una perpendicolare a ogni piano del reticolo diretto; si limiti quindi ogni perpendicolare a un segmento di lunghezza uguale al reciproco della distanza interplanare di quei particolari piani; si ponga un punto alla fine di ogni segmento di perpendicolare. Questi punti formano un reticolo chiamato ‛reciproco'. I lati e gli angoli della cella elementare del reticolo diretto vengono di regola designati con lettere senza asterisco (a, b, c, α, β, γ) , mentre per i corrispondenti elementi della cella del reticolo reciproco si usano simboli con asterisco (a*, b*, c*, α*, β*, γ*). Ogni cella può essere trasformata facilmente dallo spazio diretto a quello reciproco (e viceversa) usando i vettori fondamentali a, b, c, che delimitano una cella e i prodotti vettoriali

dove V indica il volume della cella. Si noti che questa trasformazione è reversibile, cioè (a*)* = a, (b*)* = b e (c*)* = c.

Il reticolo reciproco fornisce un metodo pratico ed efficace per l'analisi geometrica della condizione di Bragg per la diffrazione della radiazione. Riscriviamo infatti l'equazione nella forma

dove hkl indica un punto nel reticolo reciproco caratterizzato dal vettore di lunghezza 1/d_(hkl). Dal momento che d è periodico, gli ordini più alti di diffrazione (n = 2, 3, ...) sono equivalenti a un multiplo del vettore del reticolo reciproco e possono perciò essere ignorati, per cui la condizione di Bragg può essere ridotta a n = 1:

In fig. 10 viene mostrata un'interpretazione geometrica diretta di questa relazione. In questo caso θ è rappresentato dall'angolo tra il diametro di una circonferenza di raggio 1/λ e la linea che raggiunge la punta del vettore d*_(hkl) del reticolo reciproco. Possiamo ora prendere AO come direzione del fascio di raggi X incidente; θ è l'inclinazione del piano cristallino in condizioni di diffrazione; OP è la normale al piano di diffrazione ed è pertanto la direzione del vettore che va dall'origine del reticolo reciproco al punto del reticolo che rappresenta questo piano. Il vettore tracciato dal centro della circonferenza al punto del reticolo reciproco P_(hkl) rappresenta la direzione del raggio diffratto.

Questa costruzione è dovuta a P. P. Ewald (v., 1921) e la sfera, chiamata ‛sfera di Ewald', contiene l'origine del reticolo reciproco. La diffrazione avviene quando un punto del reticolo è situato sulla sfera di Ewald, le direzioni del raggio incidente e del raggio diffratto essendo ricavate come descritto prima. Tutti i movimenti geometrici del cristallo possono ora essere visualizzati facilmente attraverso rotazioni del reticolo reciproco rispetto alla sfera di Ewald. Cambiare λ significa semplicemente cambiare il diametro della sfera di Ewald.

La costruzione di Ewald è indipendente dal reale meccanismo fisico del processo di diffusione. Nei casi delle diffrazioni dei raggi X e dei neutroni, la lunghezza d'onda reciproca 1/λ ≈ 1 Å^-1 è dello stesso ordine di grandezza della distanza tra i punti del reticolo reciproco, per cui la curvatura della sfera di Ewald è considerevole. Nella diffrazione elettronica, invece, dove 1/λ ≈ 25 Å^-1, il raggio della sfera di Ewald è molto grande rispetto alle dimensioni del reticolo reciproco. Ogni volta che avviene diffrazione perché un punto del reticolo reciproco tocca la sfera di Ewald, l'intorno della sfera di Ewald visto da quel punto appare piatto. Altri punti del reticolo sullo stesso strato parallelo alla superficie della sfera di Ewald saranno anch'essi in condizioni di diffrazione, cosicché la diffrazione elettronica avviene più per piani del reticolo reciproco, mentre la diffrazione dei raggi X e dei neutroni ‛vede' punti del reticolo su piani differenti.

La diffrazione da cristalli singoli di una radiazione (quasi) monocromatica viene ottenuta ruotando il campione rispetto al fascio incidente e misurando l'intensità dell'onda diffratta con appropriati sistemi di rivelazione. Allo scopo di ottenere facilmente una vasta gamma di configurazioni di diffrazione, le apparecchiature sono progettate in modo da consentire diversi movimenti del campione. Nella fig. 11 viene mostrato un apparecchio piuttosto sofisticato, la cui geometria di diffrazione è schematizzata nella fig. 12. In questo strumento la radiazione del tubo a raggi X viene focalizzata, per mezzo di un monocromatore curvo, su un campione montato su una testina goniometrica che permette la sua rotazione intorno a tre assi con un'elevata precisione angolare. Il campione può essere traslato lungo due direzioni ortogonali per verificare, ad esempio, l'omogeneità di un cristallo. La radiazione diffratta viene raccolta da un rivelatore bidimensionale sensibile alla posizione, che può anch'esso essere spostato intorno al campione secondo due assi di rotazione indipendenti. Questa apparecchiatura permette, tenendo fisso il rivelatore, l'analisi di un tipico cristallo inorganico (come ad esempio il quarzo) in pochi minuti; è anche ideale per la misura di segnali di diffrazione diffusi dovuti a imperfezioni reticolari o a vibrazioni atomiche.

Finora sono stati presi in considerazione eventi di diffusione singoli, cioè si è partiti dal presupposto che il raggio diffratto non interagisse di nuovo con il cristallo. Questo presupposto viene definito ‛approssimazione cinematica' ed è valido quando l'ampiezza della radiazione diffusa da un atomo è molto piccola rispetto all'ampiezza della radiazione del fascio incidente. L'ampiezza di un raggio diffratto in una particolare direzione dipende in gran parte dalla possibilità che si verifichi una diffusione con interferenza da parte di un piano di atomi, così come si è supposto nell'effettuare la costruzione della sfera di Ewald. Se, come nel caso dei raggi X e dei neutroni, l'interazione con gli atomi è sufficientemente debole da far sì che l'energia diffratta sia concentrata, per ogni geometria di diffrazione, in una o due direzioni ben definite prima che il fascio primario abbia perso molta della sua energia, allora è possibile avere diffusione multipla solo nel caso di raggi che seguono queste direzioni ben definite. Un raggio diffratto può essere diffratto nuovamente se passa attraverso un'altra zona del cristallo posizionata in modo tale da soddisfare la condizione di Bragg. Nel caso di un cristallo perfetto e di una riflessione intensa la diffusione multipla diviene apprezzabile, con i raggi X, per lunghezze di cammino dell'ordine di 1 µm. Con i neutroni sono necessarie lunghezze di cammino molto maggiori. Nel caso degli elettroni, l'interazione con gli atomi è molto più forte e la diffusione multipla è generalmente molto importante. La lunghezza di cammino caratteristica è in questo caso di alcune centinaia di Å per gli atomi leggeri e ancora meno per gli atomi pesanti. In questo caso l'interazione tra la diffrazione primaria e quella secondaria può cambiare drasticamente lo spettro di diffrazione (si tratta della cosiddetta ‛diffusione dinamica', dove il termine ‛dinamica' qui usato non deve essere confuso con un'indicazione del movimento degli atomi).

L'intensità I del raggio diffratto viene ricavata direttamente dalla figura d'interferenza e può essere descritta come

I (q) = ψψ*, (q) = ∣F (q)∣² • S (q),

dove ψ è l'ampiezza del raggio diffratto e S (q) è la funzione di diffusione che contiene l'informazione sulle proprietà fisiche del processo di diffusione. Lo spettro di diffrazione è determinato principalmente dalla ‛ampiezza di struttura' (o ‛fattore di struttura') F (q), che per un reticolo (q = (h, k, l,)) è:

dove ρ (x, y, z,) è la funzione della densità atomica che è determinante per il processo di diffusione. Lo scopo dell'analisi strutturale cristallografica è di determinare ρ. La correlazione diretta tra I e ρ è uno dei mezzi più importanti ed efficaci per raggiungere questo risultato. Si noti, comunque, che l'intensità osservabile è data da ∣F_hkl∣² e non da F_hkl. Le fasi η (hkl) di F_hkl = ∣F_hkl∣ exp [iη(hkl)] non possono influenzare le intensità dovute alla diffusione cinematica senza assorbimento.

Sopperire alla mancanza di informazioni essenziali per ottenere ρ (r) costituisce il problema della fase nell'analisi strutturale. In linea di principio questo problema può essere risolto in molti modi (per esempio utilizzando effetti dinamici, assorbimento, ecc.). In pratica, le fasi vengono spesso ottenute tramite informazioni aggiuntive: per esempio, si fa una prima ipotesi approssimativa riguardo alla struttura cristallina e si effettuano spostamenti successivi delle posizioni atomiche fino a che si raggiunge un buon accordo tra le intensità di diffrazione calcolate e quelle osservate. Una trattazione dettagliata dei modi possibili per aggirare il problema della fase si può trovare in vari libri (v., ad es., Cowley, 1984).

A differenza dei raggi X, i neutroni sono particelle con spin 1/2, per cui la loro sezione efficace di diffusione da parte di un cristallo avente momenti magnetici dipenderà in generale dall'orientamento relativo tra i momenti magnetici stessi e lo spin del neutrone. In alcuni casi questa dipendenza può essere così forte che la sezione efficace di diffusione è significativa solo per un particolare stato di spin incidente. In tal caso, questi bersagli del fascio neutronico possono essere utilizzati come polarizzatori per il fascio stesso ed essere impiegati sia per il raggio incidente sia per il raggio diffratto. La diffusione da parte dei vari siti presenti in una struttura cristallina non dipenderà solo dagli atomi e dalle loro posizioni relative, ma anche dal loro momento magnetico. Sono perciò siti realmente equivalenti solo quelli equivalenti non solo per posizione ma anche per momento magnetico. La descrizione teorica, mediante la teoria dei gruppi, viene quindi basata sui gruppi spaziali ‛colorati'.

4. Transizioni di fase strutturali

Verso gli anni cinquanta, la sempre maggiore precisione delle analisi strutturali rese evidente che le strutture cristalline rappresentano quantità termodinamiche, cioè esse variano al variare di temperatura, pressione, ambiente chimico, ecc. Molti cambiamenti strutturali sono abbastanza facili da capire, come ad esempio il fatto che vi sia un'espansione durante il riscaldamento, che aumenti la compattezza quando si applica una pressione esterna e che si verifichino sostituzioni atomiche quando si ha una variazione della composizione chimica. La determinazione dei parametri fisici corrispondenti è perciò divenuta un'attività usuale dei cristallografi.

Cambiamenti strutturali più fondamentali possono comportare modificazioni topologiche della struttura cristallina e/o cambiamenti di simmetria. Tali cambiamenti definiscono le ‛fasi', nel senso termodinamico. I cambiamenti che avvengono tra l'una e l'altra di tali fasi sono chiamati ‛transizioni di fase strutturali' (v. Bruce e Cowley, 1981; v. Khachaturyan, 1983; v. Salje, 1993). Un tipico esempio di transizione di fase tra una struttura esagonale (ad alte temperature) e una struttura trigonale (a basse temperature) nel quarzo (SiO²) è mostrato nella fig. 13. Piccole rotazioni dei tetraedri SiO⁴ indotte dal raffreddamento distruggono la simmetria esagonale e producono una disposizione più compatta dei tetraedri, stabile a bassa temperatura. L'ampiezza della rotazione dei tetraedri aumenta progressivamente col diminuire della temperatura, mentre non si osservano variazioni di orientazione per temperature al di sopra del punto di transizione. Tale meccanismo di transizione, con uno spostamento graduale - e nella maggior parte dei casi molto piccolo - degli atomi, viene chiamato ‛di spostamento' (displacive, in inglese). Una definizione più precisa delle transizioni di spostamento si basa sull'apparizione di fononi soffici come eccitazione fondamentale di tali sistemi.

Si possono verificare rotture di simmetria anche tramite molti altri meccanismi. Uno dei più comuni comporta l'ordinamento di cationi o anioni differenti in vari siti della struttura cristallina ed è spesso osservato nelle leghe, che possono presentare una distribuzione disordinata di atomi metallici come Cu e Au ad alta temperatura, ma una struttura ordinata a bassa temperatura. Un altro esempio, più simile a quello del quarzo, è la struttura dei feldspati. In fig. 3 è mostrata la conformazione del feldspato ad alta e a bassa temperatura; in tutti e due i casi la struttura è costituita da tetraedri di atomi di ossigeno contenenti al centro un catione, che può essere Al o Si. Ad alta temperatura Al e Si sono disordinati; a bassa temperatura sono ordinati. L'ordinamento comincia a una temperatura di transizione ben definita. Il grado di ordine aumenta via via che la temperatura si abbassa. Si noti che i tetraedri di AlO⁴ e SiO⁴ hanno dimensioni differenti, per cui l'ordinamento di Al e Si è accompagnato da una deformazione locale nella struttura là dove avviene l'ordinamento atomico. Le transizioni di fase strutturali il cui meccanismo essenziale è legato a cambiamenti dell'ordinamento atomico sono generalmente chiamate di ‛ordine/disordine' (o semplicemente ‛od').

Esistono molti altri meccanismi di transizione e ad agire come variabile principale per la transizione non è solo la temperatura, ma anche la pressione, oppure le variazioni nella composizione chimica, ecc. Inoltre, tutti questi meccanismi possono interagire, per cui i materiali spesso mostrano transizioni di fase strutturali che risultano dalla sovrapposizione di diversi meccanismi che si influenzano reciprocamente. Uno dei primi e più essenziali compiti della ricerca cristallografica sulle transizioni di fase è quello di distinguere le alterazioni della struttura cristallina indotte da ciascuna di esse (v. Bruce e Cowley, 1981; v. Khachaturyan, 1983; v. Salje, 1992 e 1993).

Una condizione fondamentale su cui si basa la possibilità che avvenga una transizione di fase strutturale è legata alla compensazione di due contributi all'energia libera di Gibbs, che deve essere al suo valore minimo per tutte le variazioni dei parametri strutturali, se la struttura cristallina risulta termodinamicamente stabile. Una transizione di fase strutturale tra due strutture 1 e 2 avviene quando l'energia libera di Gibbs della struttura cristallina 1 è più bassa - poniamo - alle temperature più basse, mentre l'energia libera di Gibbs della struttura cristallina 2 è più bassa ad alte temperature. Il riscaldamento del cristallo produrrà una transizione strutturale dalla fase 1 alla fase 2, a meno che il processo di transizione non sia cineticamente impedito. Lo stesso fenomeno si verifica quando si cambiano altri parametri termodinamici esterni, quali pressione, composizione chimica, ecc. Dal momento che non è l'energia libera di Gibbs totale che conta per la stabilità di una struttura, ma piuttosto la differenza che esiste tra le energie libere di Gibbs delle diverse strutture in competizione, tutte le quantità termodinamiche sono misurate come differenze di questo tipo (le cosiddette ‛quantità in eccesso'). L'energia libera di Gibbs (in eccesso) può essere scomposta nella entalpia H (in eccesso) e nella entropia S (in eccesso): G = = H - TS. G può cambiare di segno quando il termine TS diventa più grande o più piccolo di H. Un semplice modello atomico può illustrare questo meccanismo. Consideriamo anzitutto i potenziali locali a cui si trovano gli atomi. Questi potenziali sono generalmente anarmonici, per cui i loro centri non sono necessariamente situati in corrispondenza di un minimo energetico. Aggiungiamo ora l'interazione tra i movimenti degli atomi introducendo un accoppiamento tra le posizioni atomiche. Nelle transizioni di fase strutturali questo accoppiamento viene raggiunto in prevalenza tramite una deformazione elastica della struttura (stress strutturale), oppure tramite forze elettriche dipolari. In entrambi i casi, comunque, l'interazione efficace diminuisce all'aumentare della distanza R come 1/R³. L'esistenza di questa interazione a lungo raggio e la sua forte direzionalità (a differenza del modello di Ising in cui si tiene conto solo dell'interazione fra primi vicini) ci permettono di considerare l'effetto complessivo di tutte le interazioni agenti su un atomo come un campo (il ‛campo medio') e di descrivere l'accoppiamento interatomico come una semplice molla. L'energia totale di questa configurazione è esprimibile come somma dell'energia cinetica, dell'energia potenziale locale e dell'energia di accoppiamento come descritto dalla hamiltoniana efficace

dove M è la massa atomica efficace, P la quantità di moto, Ω_ol la frequenza locale delle piccole oscillazioni intorno al minimo del potenziale locale, u tiene conto della anarmonicità e le υ_ll′ sono le costanti di accoppiamento che si manifestano perché l'interazione ha luogo tra siti differenti.

L'energia libera di Gibbs, G, può essere allora calcolata o almeno approssimata. Si ha la transizione di fase strutturale quando G cambia di segno, essendo il parametro di ordine strutturale Q - che è il valore di Q_l per il movimento atomico rilevante - uguale a 0 nella fase ad alta simmetria e diverso da 0 (e in graduale aumento) nella fase a bassa simmetria.

Esistono soluzioni approssimate dell'hamiltoniana che valgono per tre regimi, ciascuno dei quali è caratterizzato da un valore diverso del parametro Δ = u/(MΩ0²) - 1 (in cui υ e Ω₀ sono i valori rispettivamente di υ_ll′ e Ω_ol per il movimento atomico rilevante) che viene preso a misura dell'accoppiamento tra i siti rispetto alla parte parabolica del potenziale nel sito. Si definiscono, inoltre, due temperature: la prima, T^c, è la temperatura critica al di sotto della quale la fase ad alta simmetria diviene instabile; la seconda, θ_s = ½ (ℏ/k_B) Ω₀, è quella al di sotto della quale le fluttuazioni termiche risultano saturate (mentre per T ≫ θ_s le fluttuazioni aumentano linearmente con la temperatura).

Le tre soluzioni più comunemente utilizzate per l'analisi dei dati sperimentali sono: 1) transizioni di fase di spostamento, che hanno 0 ≾ Δ ≪ 1, in cui

che diventa (quando θ_s ≪ T) il potenziale di Landau

2) transizioni quasi di spostamento, in cui Δ ≾ 1, che non hanno però soluzioni analitiche e devono essere risolte numericamente per ottenere il valore del parametro d'ordine strutturale Q a ciascuna temperatura T. Le curve di Q in funzione di T che ne risultano hanno valori di Q più piccoli verso le basse temperature rispetto alla prima soluzione; 3) transizioni ordine/disordine, descritte abbastanza bene dall'equazione di Bragg-Williams,

In molti casi, la teoria di Landau rappresenta una buona approssimazione per T ≫ θ_s e perciò riportiamo le espressioni analitiche per la dipendenza dalla temperatura del parametro d'ordine Q per il potenziale di Landau:

a) una transizione del ‛secondo ordine':

b) una transizione ‛tricritica':

c) una transizione del ‛primo ordine':

per

Esistono inoltre altri potenziali di Landau che includono termini di ordine dispari (quando sono compatibili con la simmetria del cristallo) o termini di ordine più alto: tutti portano a espressioni simili della funzione Q(T).

I dati sperimentali spesso seguono in modo soddisfacente la dipendenza di Q dalla temperatura prevista dalla teoria, in particolare per le trasformazioni di fase di spostamento. Di fatto, l'applicabilità della forma generalizzata della teoria di Landau è molto più vasta di quanto previsto originariamente (v. Landau e Lifsič, 1938), anche per i regimi termici con parametri d'ordine vicini all'unità. Inoltre, le transizioni di fase strutturali il cui parametro d'ordine si annulla in modo progressivo quando la sostanza viene riscaldata attraverso il punto di transizione (casi a e b) non mostrano necessariamente gli effetti delle fluttuazioni critiche, contrariamente alle transizioni di fase caratterizzate da interazioni a corto raggio come quelle descritte dal modello di Ising.

Nella discussione delle varie strutture cristalline e della loro stabilità termodinamica ci siamo limitati a considerare il parametro d'ordine Q come misura del cambiamento strutturale quando da una struttura si passa a un'altra. Il parametro d'ordine, che è pertanto la quantità più importante per descrivere il processo di transizione, viene introdotto come misura della deviazione dello stato strutturale della fase a bassa simmetria (Q ≠ 0) rispetto a quello della fase ad alta simmetria (Q = 0). Esso vale per tutte le transizioni di fase nelle quali una struttura ha un gruppo spaziale che è un sottogruppo di quello dell'altra fase. Il suo significato deriva da esigenze termodinamiche, e perciò non è sempre ovvio in che misura il parametro d'ordine sia legato alle grandezze strutturali che conservano la generale topologia strutturale della fase ad alta simmetria. Alcuni elementi di simmetria della fase ad alta simmetria spariscono, cioè vengono ‛rotti', durante la transizione di fase, e ciò rende necessario introdurre un ulteriore parametro che specifichi lo stato termodinamico della struttura a bassa simmetria.

Illustriamo questa necessità attraverso l'esempio del quarzo (v. fig. 13). Nella forma ad alta simmetria l'orientazione dei tetraedri mediata nello spazio e nel tempo è completamente determinata dalla simmetria della struttura cristallina. Nella struttura a bassa simmetria questo non è più vero, perché la simmetria è ridotta e pertanto piccole rotazioni dei tetraedri risultano compatibili con i vincoli imposti dalla simmetria. Per caratterizzare la fase a bassa simmetria dobbiamo perciò specificare di quanto siano ruotati i tetraedri e in quale direzione.

Analogamente, la fase ad alta simmetria della struttura dei feldspati impone che Al e Si siano distribuiti nei tetraedri in modo casuale. Nella struttura a bassa simmetria questa distribuzione non è più casuale, ma alcuni siti strutturali sono occupati di preferenza da Al e altri da Si (che sono perciò ordinati). Di nuovo, dobbiamo specificare fino a che punto è avvenuto questo ordinamento nei siti.

Per mettere in relazione il parametro d'ordine Q con le proprietà termodinamiche del materiale, notiamo semplicemente che l'energia libera di Gibbs, G, deve dipendere da T, P... e in particolare da Q secondo una funzione del tipo G (T, P, ..., Q). Con Q = 0, nella fase di alta simmetria, possiamo definire ΔG = G - G (Q = 0) come ‛energia libera di Gibbs in eccesso'. Analogamente, si usa definire tutte le altre quantità fisiche come ‛in eccesso' rispetto al loro stato definito da Q = 0. Una volta che la dipendenza di ΔG da Q sia stata determinata, sperimentalmente o attraverso modelli fenomenologici, la dipendenza di Q da P, T... viene ricavata semplicemente dalla condizione di equilibrio, che impone che G sia al suo valore minimo al momento in cui Q è al suo valore di equilibrio, cioè quando dG/dQ = 0, d²G/dQ² > 0. Tutti gli altri parametri fisici sono allora determinati attraverso la loro relazione con Q.

Per definire il parametro d'ordine è essenziale che esista una stretta relazione strutturale tra le due fasi. Questo ci permette di definire una precisa ‛struttura della differenza', che è la differenza tra la vera struttura cristallina che stiamo esaminando e la struttura di alta simmetria presa come struttura di riferimento. Essa descrive direttamente gli spostamenti atomici, i cambiamenti dell'occupazione dei siti, ecc. Il parametro d'ordine diviene allora l'ampiezza di questa struttura di riferimento e ci dice ‛quanto avviene', mentre la struttura stessa ci dice ‛che cosa avviene'. Il parametro d'ordine è generalmente normalizzato all'unità per il valore che corrisponde al cambiamento massimo (ipotetico) possibile, mentre è 0 in assenza di cambiamenti, cioè per la fase ad alta simmetria.

La stretta relazione strutturale indicata precedentemente, comunque, può anche non esistere. Se una struttura cristallina si trasforma in un'altra senza che esista alcuna relazione topologica tra di esse, la transizione viene chiamata ‛ricostruttiva' e non può essere definito alcun parametro d'ordine se non un semplice rapporto di volume normalizzato tra le due fasi. Se le due strutture si trasformano una nell'altra tramite una relazione topologica tridimensionale ben definita, la transizione è chiamata ‛topotattica'. Nel caso di relazioni bidimensionali, la transizione strutturale è chiamata ‛epitattica'. Molti materiali mostrano una struttura a strati: se la sovrapposizione relativa dei loro strati cambia durante una trasformazione di fase, tale transizione viene chiamata ‛politipica'. Le varie strutture che possono essere messe in relazione tra loro tramite queste transizioni di fase politipiche (ipotetiche o reali) sono generalmente chiamate ‛politipi' e si distinguono in base alla differente sovrapposizione di strati identici (o quasi) che costituiscono l'unità strutturale di base. Il parametro d'ordine Q descrive in questi casi la quantità di materiale presente in una data sequenza di impilamento.

Per determinare le proprietà di simmetria di questo parametro Q sono stati usati i metodi della teoria dei gruppi. Il parametro d'ordine è una quantità scalare nel caso delle transizioni di fase tra strutture con simmetria triclina, monoclina od ortorombica. Nelle transizioni tra fasi che hanno simmetria maggiore, il parametro d'ordine può avere fino a tre componenti, Q = {Q_i}, con i ≤ 3, che rappresentano degenerazioni dei vincoli di simmetria. Ulteriori degenerazioni derivano dal fatto che, se viene distrutta la simmetria traslazionale, il parametro d'ordine è una quantità complessa, Q = Q₀ exp (- i q • r), dove q è il vettore d'onda in eccesso (si noti che se la simmetria traslazionale è conservata, si ha q = 0). Possono verificarsi degenerazioni se il vettore d'onda q descrive molti meccanismi di transizione tra loro equivalenti per simmetria.

Sono anche comuni le variazioni delle strutture cristalline nello spazio, sebbene esse non rappresentino un equilibrio termodinamico. Le perturbazioni più comuni sono le pareti tra i geminati e i bordi antifase (AntiPhase Boundaries, APB).

La comparsa di un ordinamento può permettere al cristallo di divenire eterogeneo, cioè di avere valori differenti del parametro d'ordine nei diversi dominî. Nelle transizioni di fase strutturali in cui due dominî adiacenti hanno parametri d'ordine con segno opposto, i dominî vengono chiamati ‛geminati' e sono separati tra loro da una parete. Parametri d'ordine di questo tipo normalmente comportano una grande deformazione spontanea, dove per deformazione spontanea si intende la deformazione che deve subire la struttura ad alta simmetria per trasformarsi nella fase a bassa simmetria. Questa deformazione viene raggiunta automaticamente tramite la trasformazione di fase strutturale e non per mezzo di uno sforzo esterno. Il luogo dei punti determinato dalla condizione di compatibilità tra i due geminati S¹ e S² è la loro parete di separazione.

Esistono due tipi di pareti che sono ortogonali rispetto alla fase di alta simmetria: le pareti la cui posizione è completamente specificata dai vincoli di simmetria (per esempio quelle che sono parallele ai piani di simmetria della fase di alta simmetria) sono chiamate ‛pareti W '; quelle invece che hanno dei gradi di libertà nell'orientazione sono chiamate ‛pareti W″. Si hanno pareti W′, per esempio, quando l'unico vincolo di simmetria esistente è che un asse binario della fase di alta simmetria sia contenuto nella parete; questa può allora ruotare intorno all'asse per minimizzare la sua energia. L'angolo di rotazione dipenderà, in questo caso, essenzialmente dal parametro di controllo (per esempio da T).

La struttura interna della parete fra due geminati viene generalmente ricavata dall'energia di Gibbs, (G = G (Q, T) + (½) g (∇ Q)²) ed è funzione della distanza misurata ortogonalmente alla parete. L'energia di gradiente (o ‛energia di Ginzburg') rappresenta l'energia necessaria per modificare nello spazio il parametro d'ordine. Le soluzioni dipendono dalla forma esplicita di G (Q, T) e nella maggior parte dei casi sono identiche o almeno vicine alla soluzione che si ottiene col potenziale di Landau, più semplice, in cui

dove Q⁰ è il parametro d'ordine d'equilibrio, X una coordinata ortogonale alla parete, e w è lo spessore della parete, il cui valore aumenta quanto più ci si avvicina al punto di transizione, in accordo con l'equazione

in cui

è dello stesso ordine di grandezza delle unità di ripetizione del reticolo.

Finora abbiamo parlato di transizione di fase ‛ferrodistorsive', in cui la simmetria per traslazione si mantiene nel corso della trasformazione di fase. Esistono però anche casi in cui la struttura interna della parete del geminato viene modificata in modo tale che ne risulti modificata la simmetria per traslazione e ciò avviene quando interagiscono molti parametri d'ordine. Invece di aversi una variazione continua del parametro d'ordine, da un valore di equilibrio su un lato della parete a un altro valore di equilibrio sull'altro lato, possono generarsi allora nuovi stati strutturali all'interno della parete stessa. Tali pareti vengono chiamate ‛bichirali' e le transizioni di fase che ne sono caratterizzate si chiamano ‛antiferrodistorsive'. Sono proprio esse che possono determinare la formazione di limiti antifase (APB) in corrispondenza dei quali la simmetria traslazionale è rotta. Nei casi in cui si abbia un debole accoppiamento deformativo, gli APB migrano attraverso il cristallo senza assumere orientazione preferenziale. Un aumento dell'accoppiamento deformativo, però, causa una loro orientazione preferenziale e fenomeni di agganciamento lungo direzioni ottimali. Lo spessore dell'APB è dell'ordine delle distanze interatomiche.

Le transizioni di fase strutturali aumentano i rilassamenti strutturali in vicinanza delle superfici e delle interfacce. Nel caso delle interfacce, tali rilassamenti appaiono come ondulazioni del parametro d'ordine e decrescono in modo esponenziale man mano che ci si allontana dall'interfaccia. La loro lunghezza caratteristica aumenta quanto più si è vicini al punto di transizione. Nel caso delle superfici, esse mostrano rilassamenti aggiuntivi, tanto nella fase ad alta quanto in quella a bassa simmetria, che agiscono come fenomeni precursori, sebbene i modi di rilassamento non siano necessariamente identici alla figura di deformazione che presenterà poi la transizione di fase. Studi teorici sembrano indicare una prevalenza di rilassamenti incommensurati e formazione di motivi quasi-periodici anche quando la transizione di fase è commensurata (v. Houchmanzadeh e altri, 1992).

5. Conclusioni e prospettive

La cristallografia si è evoluta trasformandosi da attività prescientifica di collezione e commercio di cristalli rari qual era in una scienza oggi rilanciata dalla sua capacità sperimentale e teorica di analizzare lo stato cristallino. Il primo stadio del lavoro di ricerca quantitativo e sistematico fu dominato dallo studio delle caratteristiche morfologiche e ottiche dei cristalli. Il salto di qualità che ha portato al periodo di maggiore attività della cristallografia avvenne con l'analisi quantitativa delle strutture atomiche. Il quesito più importante che fu posto durante la prima metà del XX secolo era dove fossero posizionati gli atomi in una struttura inorganica. Un altissimo numero di strutture cristalline venne risolto e ne derivò un'enorme quantità di conoscenze sui modi più adatti di descrivere, classificare e identificare queste strutture. Tale approccio fu in seguito esteso a materiali organici e a campioni biologici. La stridente diversità di queste strutture e il loro eccezionale interesse a scopi commerciale, medico e genetico permise ai cristallografi di trovare un ampio campo di applicazioni per le loro attività tradizionali. Parallelamente, cristalli liquidi e strutture incommensurate e non periodiche divennero un'importante area nella ricerca fisica, chimica e nella scienza dei materiali. Altre strutture ancora più complesse si generano nei processi geologici, e anch'esse devono essere analizzate coi metodi della ricerca cristallografica.

L'analisi strutturale coi raggi X fu poi integrata con altre tecniche sperimentali, come la diffrazione neutronica dinamica, la spettroscopia Raman e infrarossa per l'analisi dei fononi e di altre eccitazioni dinamiche dei cristalli, lo studio dei difetti, delle interfacce e delle superfici tramite tecniche diffrattometriche avanzate e misure delle proprietà elettriche, magnetiche ed elastiche dei cristalli. Tutte queste attività portarono a una forte diversificazione della cristallografia e all'integrazione della cristallografia con altre discipline. Il forte legame tradizionale tra la cristallografia e la mineralogia e, più in generale, le scienze della Terra non ebbe più lo stesso status esclusivo, mentre crebbero velocemente i legami con le scienze biologiche, fisiche e dei materiali. Sembra ora apparire all'orizzonte un legame perfino più stretto con l'ingegneria tecnica. Comunque, carattere comune a tutte le ricerche cristallografiche rimane l'interesse per la disposizione geometrica degli atomi in un materiale e il suo significato per le proprietà che quel materiale presenta. Definita in questo modo, la cristallografia ha espanso continuamente il suo campo di applicazione, sebbene una buona parte di essa non venga più chiamata cristallografia neppure dai suoi addetti.

BIBLIOGRAFIA

Bradley, C. I., Cracknell, A. P., The mathematical theory of symmetry in solids: representation theory for point groups and space groups, Oxford 1971.

Bragg, W. L., The diffraction of short electromagnetic waves by a crystal, in ‟Proceedings of the Cambridge Philosophical Society", 1913, XVII, pp. 43-57.

Bravais, M. A., Études cristallographiques, Paris 1866.

Bruce, A. D., Cowley, R. A., Structural phase transitions, London 1981.

Buerger, M. J., X-ray crystallography, London 1942.

Cowley, J. M., Diffraction physics, Amsterdam 1984.

Ewald, P. P., Das ‟reziproke" Gitter, in ‟Zeitschrift für Kristallographie", 1921, LVI, pp. 148-150.

Fedorov, E. S., Simmetrija i struktura kristallov, Moskva 1949.

Heine, V., Group theory in quantum mechanics, New York 1963.

Hermann, C., Kristallographie in Räumen beliebiger Dimensionszahl, in ‟Acta crystallographica", 1949, II, pp. 139 ss.

Houchmanzadeh, B., Lajzerowicz, J., Salje, E., Relaxations near surfaces and interfacies for first, second and third neighbor interactions: theory and applications for polytypism, in ‟Journal of physics: condensed matter", 1992, IV, pp. 9779 ss.

Khachaturyan, A. G., Theory of structural transformations in solids, New York 1983.

Landau, L. D., Lifsič, E. M., Statističeskaja fizika, Moskva 1938 (tr. it.: Fisica statistica, Roma 1978).

Laue, M. von, Eine quantitative Prüfung der Theorie für die Interferenzerscheinungen bei Röntgenstrahlen, in ‟Sitzungsberichte der Königlichen Bayerischen Akademie der Wissenschaften zu München", 1912, pp. 363-373.

Ljubarskij, G. J., Teorija gruppi eë primenenie v fizike, Moskva 1957 (tr. ingl.: The application of group theory in physics, New York 1960).

Salje, E. K. H., Application of Landau theory for the analysis of phase transitions in minerals, in ‟Physics reports", 1992, CCXV, 2, pp. 49-99.

Salje, E. K. H., Phase transitions in ferroelastic and co-elastic crystals, Cambridge 1993.

Šubnikov, A. V., Simmetrija i antisimmetrija konečnych figur, Moskva 1951.

Šubnikov, A. V., Koptsik, V. A., Simmetrija v nauke i iskusstve, Moskva 1972 (tr. ingl.: Symmetry in science and art, New York 1974).