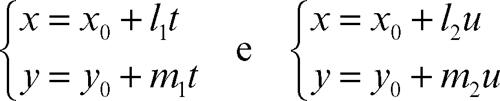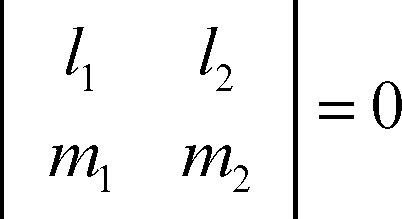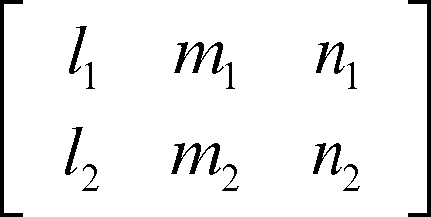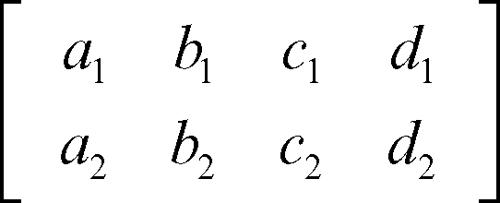parallelismo, criteri di
parallelismo, criteri di
parallelismo, criteri di condizioni che permettono di stabilire il parallelismo tra due rette, tra una retta e un piano o tra due piani. L’esempio più semplice riguarda il parallelismo tra rette nel piano: due rette r e s complanari sono parallele se e solo se, tagliate da una retta trasversale, verificano una delle seguenti condizioni:
• formano angoli alterni interni (o esterni) di uguale ampiezza;
• formano angoli corrispondenti di uguale ampiezza;
• formano angoli coniugati interni (o esterni) supplementari.
(→ angoli associati (rispetto a due parallele)). Se le rette r1 e r2, sono date, in un riferimento cartesiano, rispettivamente mediante le equazioni y = m1x + q1 e y = m2x + q2, oppure mediante le equazioni a1x + b1y + c1 = 0 e a2x + b2y + c2 = 0, esse risultano parallele se e solo se si ha m1 = m2 o, in termini dei coefficienti, se a1b2 − a2b1 = 0. Se le rette r1 e r2 sono invece assegnate mediante le equazioni parametriche
esse risultano parallele se e solo se risulta
Nello spazio tridimensionale due rette sono parallele se e solo se, indicati con [l1 m1 n1] e [l2 m2 n2] i rispettivi parametri direttori, il rango della matrice
è uguale a 1. Analogamente si possono assegnare condizioni analitiche per stabilire il parallelismo tra piani e il parallelismo tra retta e piano. Due piani, di rispettive equazioni a1x + b1y + c1z + d1 = 0 e a2x + b2y + c2z + d2 = 0 sono paralleli se e solo se risulta uguale a 1 il rango della matrice
Una retta di parametri direttori [l m n] e un piano di equazione ax + by + cz + d = 0 sono paralleli se e solo se al + bm + cn = 0.