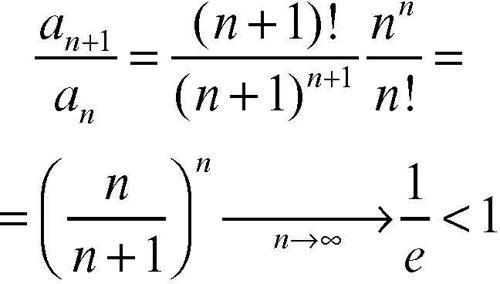Alembert, criterio di

Alembert, criterio di

Alembert (d’), criterio di o criterio del rapporto, è uno dei criteri più semplici per stabilire se una serie numerica è convergente. Data la serie

a termini strettamente positivi, si consideri il rapporto a_n+1/a_n tra due termini consecutivi. Se esistono una costante k < 1 e un indice n₀ tale che, per n > n₀, risulti sempre a_n+1/a_n ≤ k, la serie converge; se invece a_n+1/a_n ≥ 1, la serie diverge. Il criterio si utilizza, di solito, nella forma più restrittiva seguente: posto

se l < 1 la serie converge, se l > 1 o = 1⁺, la serie diverge. Per esempio, la serie

converge, perché il rapporto

Questo criterio è tuttavia poco potente, perché molte serie significative non soddisfano né alla condizione per la convergenza né a quella per la divergenza: a esso sfuggono tutte le serie per cui l = 1⁻ che è il caso più interessante (→ limite). Per esempio, le serie del tipo

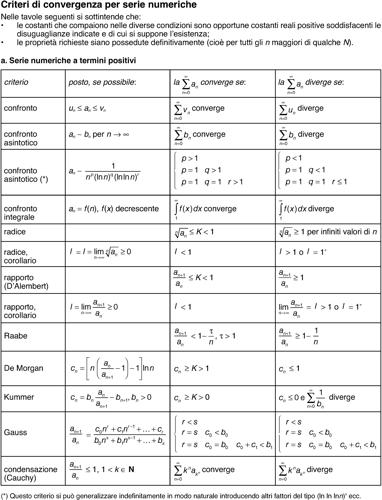
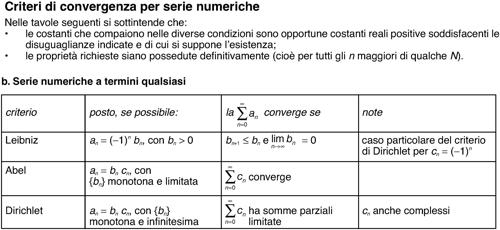
con p > 0, ammettono tutte limite l = 1⁻, ma di esse convergono solo quelle con p > 1 (→ serie numerica, criteri di convergenza per una; si veda anche le relative tavola).