Dirichlet, criterio di
Dirichlet, criterio di
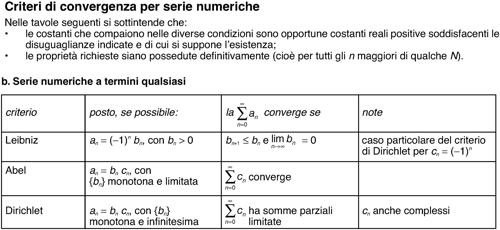
Dirichlet, criterio di criterio di convergenza per una serie numerica a termini qualsiasi, utilizzabile anche per serie di funzioni. Sia data la serie numerica
i cui termini si possono esprimere nella forma an = bncn, tali che la successione {bn} sia monotòna e infinitesima e che la serie
abbia somme parziali limitate; il criterio di Dirichlet stabilisce che in queste condizioni la serie data converge. Nel caso di serie di funzioni, se an(x) = bn(x)cn(x), l’uniforme convergenza della
in un insieme E si deduce dalle due ipotesi seguenti:
1) che la successione {bn(x)} sia monotòna per ogni x ∈ E ed infinitesima, uniformemente in E;
2) che le somme parziali di
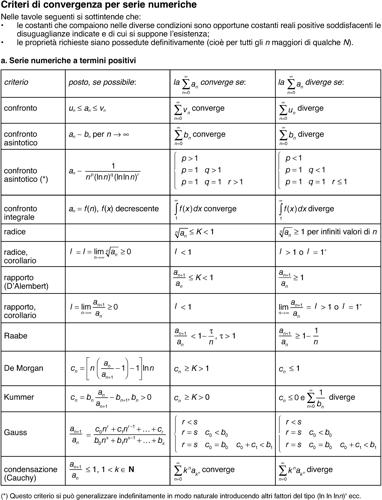
siano uniformemente limitate in E. Si veda la tavola dei criteri di convergenza per una serie numerica.