Kummer, criterio di
Enciclopedia della Matematica (2013)
Kummer, criterio di
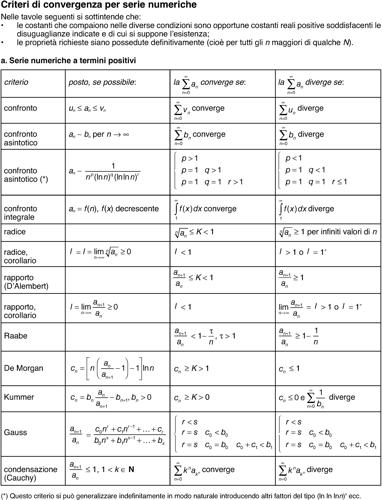
Kummer, criterio di criterio di convergenza per serie a termini positivi. La serie
converge se si può trovare una opportuna successione {bn} di numeri strettamente positivi e una costante ρ > 0 tali che, posto
risulta cn ≥ ρ definitivamente (cioè a partire da un certo n). Si può anche porre
La serie invece diverge se si ha cn ≤ 0 e
diverge. Ponendo bn = n si ottiene il criterio di → Raabe, mentre con bn costantemente uguale a 1 si ha il criterio del confronto (si vedano le tavole dei criteri di convergenza per serie numeriche).