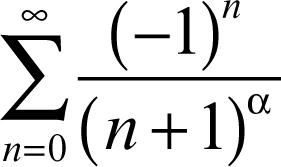Leibniz, criterio di
Leibniz, criterio di
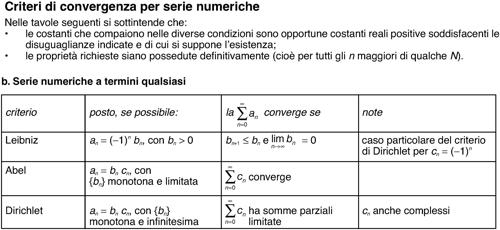
Leibniz, criterio di criterio di convergenza per una serie numerica a termini di segno alternato. La serie
converge se la successione {bn} dei valori assoluti dei suoi termini è decrescente e infinitesima e ha limite zero, cioè se bn+1 ≤ bn e
Le somme parziali ottenute approssimano la somma della serie alternativamente per eccesso e per difetto, rispettivamente se l’ultimo termine sommato è positivo o negativo. L’errore commesso non supera, in modulo, il primo termine che si trascura. Per esempio, la serie armonica generalizzata a segni alternati
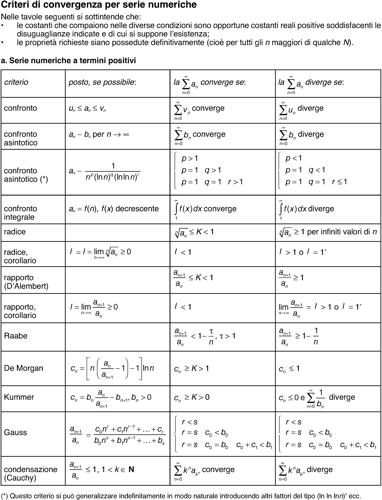
converge per ogni valore di α > 0, anche se è praticamente inutilizzabile per il calcolo numerico data la lentezza della sua convergenza per α piccolo (si vedano le tavole dei criteri di convergenza per serie numeriche).